Исследование поведения функции
3.1. Промежутки постоянства и монотонности
Пусть 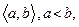 - некоторый промежуток, ограниченный или неограниченный.
- некоторый промежуток, ограниченный или неограниченный.
Теорема 1. ( Критерий постоянства функции на промежутке)
Пусть функция f непрерывна на  и дифференцируема на (a,b). Для того, чтобы f(х) тождественно на
и дифференцируема на (a,b). Для того, чтобы f(х) тождественно на  была равна константе, необходимо и достаточно, чтобы её производная тождественно на (a,b) была равна нулю:
была равна константе, необходимо и достаточно, чтобы её производная тождественно на (a,b) была равна нулю:
► Необходимость. Пусть f(х) 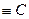 на (a,b), а х0 – произвольная точка этого интервала. При любом h, удовлетворяющем требованию х0 + h
на (a,b), а х0 – произвольная точка этого интервала. При любом h, удовлетворяющем требованию х0 + h 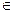 (a,b) имеем:
(a,b) имеем: 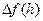 =
= 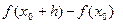 = С – С = 0; значит,
= С – С = 0; значит, 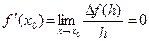 .
.
Достаточность. Пусть 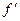 (х)
(х) 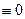 на (a,b). Выберем некоторую точку х0 на интервале (a,b) и обозначим: f(х0)
на (a,b). Выберем некоторую точку х0 на интервале (a,b) и обозначим: f(х0) 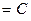 . Пусть х – произвольная точка этого интервала, отличная от х0 . На сегменте, ограниченном точками х0 и х функция f удовлетворяет всем требованиям условия теоремы Лагранжа (см. п. 2.2.) ; поэтому существует точка ξ , ле- жащая между этими точками и такая, что f(х) –f(х0)=
. Пусть х – произвольная точка этого интервала, отличная от х0 . На сегменте, ограниченном точками х0 и х функция f удовлетворяет всем требованиям условия теоремы Лагранжа (см. п. 2.2.) ; поэтому существует точка ξ , ле- жащая между этими точками и такая, что f(х) –f(х0)= 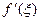 (х – х0). Ясно,что ξ
(х – х0). Ясно,что ξ 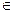 (a,b), а тогда
(a,b), а тогда 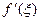 =0. Значит, f(х) =f(х0)=С; отсюда:
=0. Значит, f(х) =f(х0)=С; отсюда: 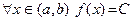 . ◄
. ◄
Теорема 2.(Критерий монотонности функции на промежутке)
Пусть функция f непрерывна на  и дифференцируема на (a,b). Для того, чтобы онабыла неубывающей (невозрастающей ) на промежутке
и дифференцируема на (a,b). Для того, чтобы онабыла неубывающей (невозрастающей ) на промежутке  , необходимо и достаточно, чтобы её производная была неотрицательной (неположительной) на интервале (a,b).
, необходимо и достаточно, чтобы её производная была неотрицательной (неположительной) на интервале (a,b).
► Необходимость. Пусть х0 –произвольная точка интервала (a,b). По условию теоремы существует производная  , значит, существует и односторонная производная справа
, значит, существует и односторонная производная справа 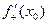 , причем
, причем  =
= 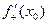 .
.
Рассмотрим случай неубывающей функции. По определению
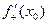 =
= 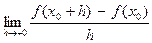 . Здесь h > 0; и так как f – неубывающая функция, то f(x0+h) – f(x0) ≥ 0; поэтому
. Здесь h > 0; и так как f – неубывающая функция, то f(x0+h) – f(x0) ≥ 0; поэтому 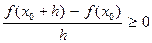 . Отсюда и из теоремы о предельном переходе в неравенстве (гл. 1, п.4.5) следует:
. Отсюда и из теоремы о предельном переходе в неравенстве (гл. 1, п.4.5) следует: 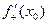 ≥ 0. Но х0 –произвольная точка интервала (a,b). Следовательно,
≥ 0. Но х0 –произвольная точка интервала (a,b). Следовательно, 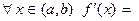
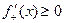 .
.
В случае невозрастающей функции аналогично покажем: 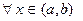
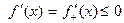 .
.
Достаточность. Пусть х1 и х2 , а≤ х1 < х2 ≤ b, - точки, произвольно выбраные на промежутке  . На сегменте [х1 , х2] функция f удовлетворяет требованиям условия теоремы Лагранжа. Запишем формулу конечных приращений: f(х2) – f(х1) =
. На сегменте [х1 , х2] функция f удовлетворяет требованиям условия теоремы Лагранжа. Запишем формулу конечных приращений: f(х2) – f(х1) = 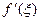 ( х2 - х1), где х1 <ξ < х2.
( х2 - х1), где х1 <ξ < х2.
Пусть 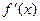 неотрицательна на (a,b). Тогда
неотрицательна на (a,b). Тогда 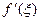 ≥ 0, и, значит, f(х1) ≤ f(х2). Таким образом, для любых х1 и х2 , а≤ х1 < х2 ≤ b, справедливо неравенство f(х1) ≤ f(х2), т.е. функция f удовлетворяет определению неубывающей на
≥ 0, и, значит, f(х1) ≤ f(х2). Таким образом, для любых х1 и х2 , а≤ х1 < х2 ≤ b, справедливо неравенство f(х1) ≤ f(х2), т.е. функция f удовлетворяет определению неубывающей на  функции.
функции.
В случае 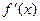 ≤ 0 на (a,b) из f(х2) – f(х1) =
≤ 0 на (a,b) из f(х2) – f(х1) = 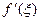 ( х2 - х1) следует: f(х1) ≥ f(х2) , значит, f удовлетворяет определению невозрастающей на
( х2 - х1) следует: f(х1) ≥ f(х2) , значит, f удовлетворяет определению невозрастающей на  функции. ◄
функции. ◄
Теорема 3.(Достаточный признак строгой монотонности) Пусть функция f непрерывна на  и дифференцируема на (a,b). Если при всех х
и дифференцируема на (a,b). Если при всех х 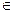 (a,b)
(a,b) 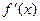 > 0 (
> 0 ( 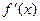 < 0 ), то функция f возрастает ( убывает ) на
< 0 ), то функция f возрастает ( убывает ) на  .
.
► Пусть х1 и х2 , а≤ х1 < х2 ≤ b, - точки, произвольно выбраные на промежутке  . На сегменте [х1 , х2] функция f удовлетворяет требованиям условия теоремы Лагранжа. Запишем формулу конечных приращений: f(х2) – f(х1) =
. На сегменте [х1 , х2] функция f удовлетворяет требованиям условия теоремы Лагранжа. Запишем формулу конечных приращений: f(х2) – f(х1) = 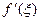 ( х2 - х1), где х1 <ξ < х2.
( х2 - х1), где х1 <ξ < х2.
Пусть 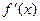 положительна на (a,b). Тогда
положительна на (a,b). Тогда 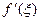 > 0, и, значит, f(х1) < < f(х2). Таким образом, для любых х1 и х2 , а≤ х1 < х2 ≤ b, справедливо неравенство f(х1) < f(х2), т.е. функция f удовлетворяет определению возрастающей на
> 0, и, значит, f(х1) < < f(х2). Таким образом, для любых х1 и х2 , а≤ х1 < х2 ≤ b, справедливо неравенство f(х1) < f(х2), т.е. функция f удовлетворяет определению возрастающей на  функции.
функции.
В случае 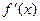 < 0 на (a,b) из f(х2) – f(х1) =
< 0 на (a,b) из f(х2) – f(х1) = 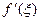 ( х2 - х1) следует: f удовлетворяет определению убывающей на
( х2 - х1) следует: f удовлетворяет определению убывающей на  функции. ◄
функции. ◄
3.2. Точки локального экстремума
Здесь мы рассматриваем следующую задачу: пусть функция f определена на некотором интервале (a,b), ограниченном или неограниченном; требуется найти точки её локальных максимумов и минимумов.
Понятие локального экстремума было введено в п. 2.1. Дополним данные там определения. Пусть функция f определена в некоторой окрестности точки х0 , х0 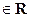 .
.
Определение. Точку х0 назовем точкой строгого локального максимума ( строгого локального минимума ) функции f , если существует δ > 0 такое, что для всякого х, принадлежащего интервалам (х9- δ, х0 ) и (х0, х0 + δ) справедливо строгое неравенство f(х) < f(х0) ( f(х) > f(х0) ) .
Согласно следствию теоремы Ферма (см. п.2.1), если функция f дифференцируема в точке х0 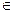 (a,b), а
(a,b), а 
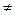 0, то х0 заведомо не может быть точкой её локального экстремума. Следовательно, отыскивая точки локальных максимумов и минимумов функции f, достаточно ограничиться рассмотрением тех точекинтервала (a,b) , в которых либо производная
0, то х0 заведомо не может быть точкой её локального экстремума. Следовательно, отыскивая точки локальных максимумов и минимумов функции f, достаточно ограничиться рассмотрением тех точекинтервала (a,b) , в которых либо производная 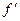 существует и равна нулю, либо производная
существует и равна нулю, либо производная 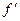 не существует. Такие точки в дальнейшем будем называть точками, подозрительными на экстремум. Если функция имеет экстремум, то только в таких точках. Покажем на примере, что подозрительная на экстремум точка не всегда оказывается на деле точкой экстремума.
не существует. Такие точки в дальнейшем будем называть точками, подозрительными на экстремум. Если функция имеет экстремум, то только в таких точках. Покажем на примере, что подозрительная на экстремум точка не всегда оказывается на деле точкой экстремума.
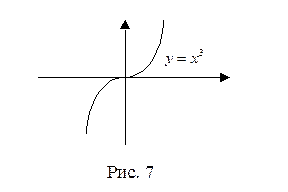 Пример 1. Пусть f(x) =x
Пример 1. Пусть f(x) =x 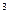 . Эта функция дифференцируема на всей числовой оси и имеет единственную подозрительную на экстремум точку:
. Эта функция дифференцируема на всей числовой оси и имеет единственную подозрительную на экстремум точку: 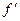 (х)= 0 только при х=0. Однако, f(x) возрастающая функция, и у нее нет точек локального экстремума (см. рис. 7).
(х)= 0 только при х=0. Однако, f(x) возрастающая функция, и у нее нет точек локального экстремума (см. рис. 7).
Таким образом, чтобы отыскать точки экстремума, следует найти подозрительные на экстремум точки, а затем для каждой из них выяснить, является ли она точкой экстремума на самом деле. Выяснить это можно с помощью достаточных признаков экстремума.
Пусть функция f определена в проколотой окрестности точки х0 .Будем говорить, что при переходе через х0 функция меняет знак с + на -, если существует δ > 0 такое, что f(х) > 0 на (х0 – δ, х0)и f(х)< 0 на (х0, х0 + +δ). Теперь понятен смысл терминов “при переходе через х0 функция меняет знак с – на + ” и “при переходе через х0 функция не меняет знак ” Например, при переходе через х0 = 0функция f(x) =x 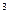 меняет знак с – на + (см. рис. 7) , а функция
меняет знак с – на + (см. рис. 7) , а функция 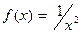 при переходе через ту же точку знака не меняет.
при переходе через ту же точку знака не меняет.
Теорема 4.(Первый достаточный признак экстремума) Пусть функция f непрерывна в некоторой окрестности точки х0 и дифференцируема в её проколотой окрестности, и пусть х0 является для f точкой, подозрительной на экстремум,. Тогда:
1) если при переходе через х0 производная 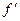 меняет знак с + на -, то х0 есть точка строгого локального максимума функции f ;
меняет знак с + на -, то х0 есть точка строгого локального максимума функции f ;
2) если при переходе через х0 производная 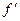 меняет знак с – на +, то х0 есть точка строгого локального минимума функции f ;
меняет знак с – на +, то х0 есть точка строгого локального минимума функции f ;
3) если при переходе через х0 производная 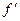 не меняет знак, то х0 не является точкой локального экстремума функции f.
не меняет знак, то х0 не является точкой локального экстремума функции f.
► 1) Существует δ > 0 такое, что f(х) > 0 на (х0 – δ, х0)и f(х)< 0 на (х0, х0 + δ). В силу критерия монотонности f не убывает на (х0 – δ, х0] и не возрастает на [х0, х0 + δ); следовательно, при всяком 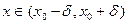
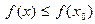 , т.е. х0 - точка локального максимума.
, т.е. х0 - точка локального максимума.
2) Доказательство здесь аналогично приведенному выше.
3) Допустим для определенности, что существует δ > 0 такое, что f(х) > 0 и на (х0 – δ, х0),и на (х0, х0 + δ). Значит, f не убывает и на (х0 – δ, х0], и на [х0, х0 + δ); т.е. f не убывает на (х0 – δ, х0+ δ); поэтому х0 не может быть точкой экстремума. ◄
Пример 2. Пусть f(x) =x 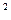 . Эта функция дифференцируема на всей числовой оси, а точка х9 =0 является подозрительной на экстремум:
. Эта функция дифференцируема на всей числовой оси, а точка х9 =0 является подозрительной на экстремум: 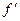 (0) = 0. При переходе через эту точку производная
(0) = 0. При переходе через эту точку производная 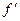 (х) = 2х меняет знак с – на +; значит, х9 =0 есть точка локального минимума.
(х) = 2х меняет знак с – на +; значит, х9 =0 есть точка локального минимума.
Пример 3. Пусть f(x) =|x| . Эта функция дифференцируема на всей числовой оси, за исключением точки х9 =0 ; 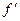 (х) ≡ -1 на (-∞ , 0) и
(х) ≡ -1 на (-∞ , 0) и 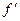 (х) ≡1 на (0,+∞). Таким образом, х9 =0 является точкой, подозрительной на экст -ремум ( в ней
(х) ≡1 на (0,+∞). Таким образом, х9 =0 является точкой, подозрительной на экст -ремум ( в ней 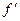 не существует), и при переходе через неё
не существует), и при переходе через неё 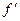 меняет знак с – на +; значит, х9 =0 есть точка локального минимума.
меняет знак с – на +; значит, х9 =0 есть точка локального минимума.
Теорема 5.(Второй достаточный признак экстремума) Пусть функция f n раз,где n> 1, дифференцируема в точке х9 , причем
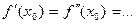
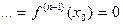 , а
, а 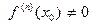 . Тогда:
. Тогда:
1) если n – четное, то х9 является точкой строгого локального экстремума, а именно, точкой строгого максимума в случае 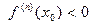 и точкой строгого минимума в случае
и точкой строгого минимума в случае 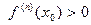 ;
;
2) если n – нечетное, то х9 не является точкой локального экстремума.
► По теореме Тейлора-Пеано
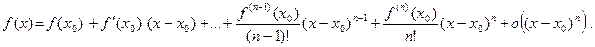 Отсюда, так как
Отсюда, так как 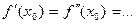
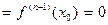 ,
,
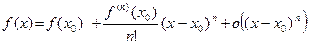 ,
,
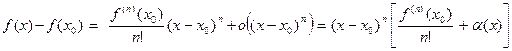 , (13) где
, (13) где 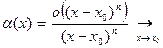 0. Пусть δ > 0 подобрано так, что при всех х, удовлетворяющих неравенствам 0< |x-x0| < δ, выполняется |
0. Пусть δ > 0 подобрано так, что при всех х, удовлетворяющих неравенствам 0< |x-x0| < δ, выполняется | 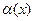 | <
| < 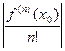 . Тогда на интервалах ( х0 - δ , х0 ) и (х0 , х0 + δ ) знак суммы в квадратных скобках (см. (13)) совпадает с знаком числа
. Тогда на интервалах ( х0 - δ , х0 ) и (х0 , х0 + δ ) знак суммы в квадратных скобках (см. (13)) совпадает с знаком числа 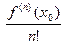 .
.
Пусть n - четное. Если 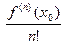 < 0, то из (13) следует, что на интервалах ( х0 - - δ , х0 ) и (х0 , х0 + δ ) разность
< 0, то из (13) следует, что на интервалах ( х0 - - δ , х0 ) и (х0 , х0 + δ ) разность 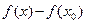 отрицательна, т. е. на этих интервалах
отрицательна, т. е. на этих интервалах 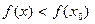 . Таким образом, если
. Таким образом, если 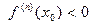 , то х0 – точ- ка строгого локального максимума (см. определение). Если же
, то х0 – точ- ка строгого локального максимума (см. определение). Если же 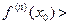 0, , то на тех же интервалах
0, , то на тех же интервалах 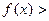
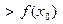 ; значит, х0 – точка строгого локального минимума.
; значит, х0 – точка строгого локального минимума.
Пусть n - нечетное. Тогда множитель 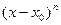 перед квадратной скобкой в (13) меняет знак при переходе через х0 ; поэтому меняет знак и разность f(x) – f( х0 ). Отсюда следует, что х0 не может бытьточкой экстремума. ◄
перед квадратной скобкой в (13) меняет знак при переходе через х0 ; поэтому меняет знак и разность f(x) – f( х0 ). Отсюда следует, что х0 не может бытьточкой экстремума. ◄
Пример 4. Пусть f(x) =x 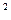 . При х0 = 0 имеем:
. При х0 = 0 имеем: 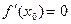 ,
, 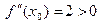 . Значит, х0 = 0 – точка строгого локального минимума.
. Значит, х0 = 0 – точка строгого локального минимума.
Пример 5. Пусть f(x) =x 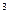 . При х0 = 0 имеем:
. При х0 = 0 имеем: 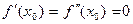 ,
, 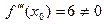 . Значит, х0 = 0 не является точкой экстремума.
. Значит, х0 = 0 не является точкой экстремума.
3.3. Промежутки выпуклости
Пустьфункция f определена на сегменте [ x1 ,x2] , x1 < x2 , и пусть
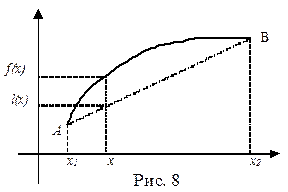
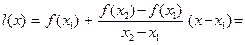
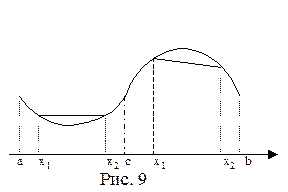 =
= 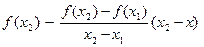 (14) Уравнение
(14) Уравнение 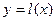 есть уравнение прямой, проходящей через лежащие на графике функции точки A(х1 ,f(x1)) и B (х2 ,f(x2)) . Если при всех х
есть уравнение прямой, проходящей через лежащие на графике функции точки A(х1 ,f(x1)) и B (х2 ,f(x2)) . Если при всех х 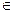 ( x1 ,x2) справедливо неравенство l(x) ≤ f(x) ( l(x) ≥ f(x) ), то график функции f(x) на интервале (x1, x2) проходит “не ниже” (“не выше” ) хорды АВ. Если же при всех х
( x1 ,x2) справедливо неравенство l(x) ≤ f(x) ( l(x) ≥ f(x) ), то график функции f(x) на интервале (x1, x2) проходит “не ниже” (“не выше” ) хорды АВ. Если же при всех х 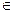 ( x1 ,x2) l(x) < f(x) ( l(x) > f(x) ), то график функции f(x) на интервале (x1, x2) проходит “строго выше” (“строго ниже” ) хорды АВ (см. рис.8).
( x1 ,x2) l(x) < f(x) ( l(x) > f(x) ), то график функции f(x) на интервале (x1, x2) проходит “строго выше” (“строго ниже” ) хорды АВ (см. рис.8).
Пустьфункция f определена на промежутке 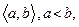 - ограниченном или неограниченном.
- ограниченном или неограниченном.
Определение. Будем говорить, что на промежутке  функция f выпукла вверх (выпукла вниз ), если при любых x1 и x2, x1 < x2 , лежащих на
функция f выпукла вверх (выпукла вниз ), если при любых x1 и x2, x1 < x2 , лежащих на  , неравенство l(x) ≤ f(x) ( l(x) ≥ f(x) ) справедливо для всякого х, принадлежащего интервалу ( x1 ,x2). Если же для всякого х, принадлежа- щего интервалу ( x1 ,x2). справедливо строгое неравенство, т.е. l(x) < f(x) ( l(x) > f(x) ), то будем говорить, что функция f строго выпукла вверх ( строго выпукла вниз) на
, неравенство l(x) ≤ f(x) ( l(x) ≥ f(x) ) справедливо для всякого х, принадлежащего интервалу ( x1 ,x2). Если же для всякого х, принадлежа- щего интервалу ( x1 ,x2). справедливо строгое неравенство, т.е. l(x) < f(x) ( l(x) > f(x) ), то будем говорить, что функция f строго выпукла вверх ( строго выпукла вниз) на  .
.
На рис.9 изображен график функции, которая строго выпукла вниз на промежутке 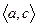 и строго выпукла вверх на промежутке
и строго выпукла вверх на промежутке 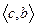 .
.
Теорема 6.(Критерий строгой выпуклости) Пусть функция f непрерывна на  и дифференцируема на (a,b). Для того,чтобы она была строго выпукла вниз ( строго выпукла вверх) на
и дифференцируема на (a,b). Для того,чтобы она была строго выпукла вниз ( строго выпукла вверх) на  , необходимо и достаточно, чтобы её производная f ′ возрастала ( убывала ) на (a,b).
, необходимо и достаточно, чтобы её производная f ′ возрастала ( убывала ) на (a,b).
Докажем критерий строгой вцпуклости вниз:
(f строго выпукла вниз на  )
) 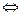 ( f ′ возрастает на (a,b) )
( f ′ возрастает на (a,b) )
► Необходимость. Пусть f строго выпукла вниз на  , т.е. при любых x1 и x2, x1 < x2 , лежащих на
, т.е. при любых x1 и x2, x1 < x2 , лежащих на  , неравенство l(x) > f(x) выполняется для всякого х, x1 < <х <x2 . Воспользовавшись первым выражением для функции l(x) (см. (14) ), неравенство l(x) > f(x) можно записать в следующем виде:
, неравенство l(x) > f(x) выполняется для всякого х, x1 < <х <x2 . Воспользовавшись первым выражением для функции l(x) (см. (14) ), неравенство l(x) > f(x) можно записать в следующем виде:
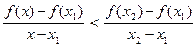 (15) Для х
(15) Для х 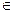 (x1 ,
(x1 , 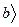 положим
положим 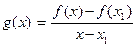 . В силу неравенства (15) имеем : на интервале (x1 ,
. В силу неравенства (15) имеем : на интервале (x1 , 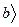 g(x) < g(x2). Заметим, что здесь х и x2 , х <x2 ,можно выбирать любыми на промежутке (x1 ,
g(x) < g(x2). Заметим, что здесь х и x2 , х <x2 ,можно выбирать любыми на промежутке (x1 , 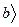 ; значит, функция g(x) возрастает на (x1 ,
; значит, функция g(x) возрастает на (x1 , 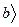 . Отсюда, и из теоремы Вейерштрасса об односторонних преде- лах монотонной функции ( [1], стр. 67)
. Отсюда, и из теоремы Вейерштрасса об односторонних преде- лах монотонной функции ( [1], стр. 67) 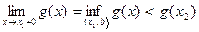 , т.е.
, т.е.
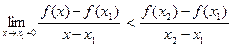 Так как f дифференцируема в точке х1 , то предел в левой части последнего неравенства равен f ′(х1), значит. f ′(х1)
Так как f дифференцируема в точке х1 , то предел в левой части последнего неравенства равен f ′(х1), значит. f ′(х1) 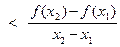 Аналогично, воспользовавшись вторым выражением для функции l(x) из (14), можно получить неравенство
Аналогично, воспользовавшись вторым выражением для функции l(x) из (14), можно получить неравенство 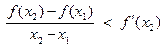 . Следовательно, при любых x1 и x2, x1 < x2 , лежащих на
. Следовательно, при любых x1 и x2, x1 < x2 , лежащих на  f ′(х1)
f ′(х1) 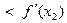 , т.е. производная f ′ возрастает на
, т.е. производная f ′ возрастает на  .
.
Достаточность. Пусть производная f ′ возрастает на  . Пусть x1 и x2, x1 < x2 , - произвольные точки на
. Пусть x1 и x2, x1 < x2 , - произвольные точки на  , а х лежит между ними: x1 < х <x2 . На каждом из сегментов [x1 , х] и [х , x2] функция f удовлетворяет всем требованиям условия теоремы Лагранжа, поэтому существуют точки
, а х лежит между ними: x1 < х <x2 . На каждом из сегментов [x1 , х] и [х , x2] функция f удовлетворяет всем требованиям условия теоремы Лагранжа, поэтому существуют точки 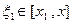 и
и 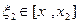 , такие, что
, такие, что
f(x)-f(x1) = f ′ 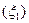 (x – x1) и f(x2) – f(x) = f ′
(x – x1) и f(x2) – f(x) = f ′ 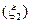 (x2 – x). Отсюда: f ′
(x2 – x). Отсюда: f ′ 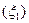 =
= 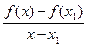 ; f ′
; f ′ 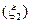 =
= 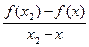 . Очевидно,
. Очевидно, 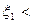
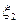 , и так как
, и так как
f ′ возрастает, то f ′ 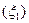 < f ′
< f ′ 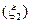 ; значит,
; значит, 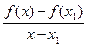 <
< 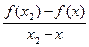 Преобразуем это неравенство:
Преобразуем это неравенство:
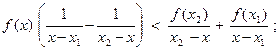 Приведя к общему знаменателю (х – х1)(х2 - х) и умножив на него обе части неравенства, получим:
Приведя к общему знаменателю (х – х1)(х2 - х) и умножив на него обе части неравенства, получим: 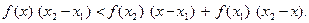 Поделим на x2 – x1 :
Поделим на x2 – x1 :
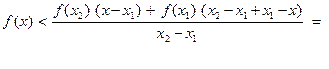

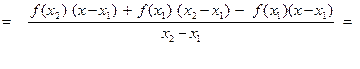
= 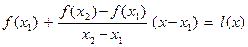 .
.
Итак , при любом х , x1 < х <x2 , выполняется f(x) < 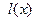 , и так как x1 и x2, x1 < x2 , - произвольные точки на
, и так как x1 и x2, x1 < x2 , - произвольные точки на  , то f выпукла вниз на
, то f выпукла вниз на  .◄
.◄
Критерий строгой выпуклости вверх
(f строго выпукла вверх на  )
) 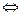 ( f ′ убывает на (a,b) )
( f ′ убывает на (a,b) )
можно доказать аналогично.
Следствие. Пусть функция f непрерывна на  и дважды дифференцируема на (a,b). Если при всех х на (a,b)
и дважды дифференцируема на (a,b). Если при всех х на (a,b) 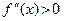 (
( 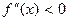 ), то f выпукла вниз (выпукла вверх ) на
), то f выпукла вниз (выпукла вверх ) на  .
.
► Действительно, 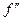 есть производная от f ′, и если при всех х на (a,b)
есть производная от f ′, и если при всех х на (a,b) 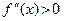 (
( 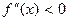 ), то в силу достаточного признака строгой монотонности (см. теорему 3) f ′ возрастает (убывает ) на (a,b) . ◄
), то в силу достаточного признака строгой монотонности (см. теорему 3) f ′ возрастает (убывает ) на (a,b) . ◄
Пример 6. Пусть f(x) =x 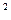 . Имеем:
. Имеем: 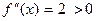 на (- ∞, +∞); значит, эта функция строго выпукла вниз на (- ∞, +∞).
на (- ∞, +∞); значит, эта функция строго выпукла вниз на (- ∞, +∞).
Пример 7. Пусть f(x) =x 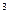 . Имеем:
. Имеем: 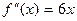 ; она отрицательна на (- ∞, 0) и положительна на (0, +∞). Следовательно, эта функция строго выпукла вверх на (- ∞, 0) и строго выпукла вниз на (0, +∞), см. рис. 7.
; она отрицательна на (- ∞, 0) и положительна на (0, +∞). Следовательно, эта функция строго выпукла вверх на (- ∞, 0) и строго выпукла вниз на (0, +∞), см. рис. 7.
3.4. Точки перегиба
Пусть функция f непрерывна в точке х0 , 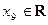 .
.
Определение. х0 назовем точкой перегиба функции f , если существу-ет δ > 0 такое, что на одном из интервалов (х0 – δ , х0) и (х0 , х0 + δ) она строго выпукла вниз, а на другом из них – строго выпукла вверх.
Таким образом, точка перегиба является общей граничной точкой двух интерва- лов, на одном из которых функция строго выпукла вниз, а на другом она строго выпукла вверх. На рис. 10 схематически изображены графики функций в окрестности точки х0 , которая для каждой из них является точкой перегиба.
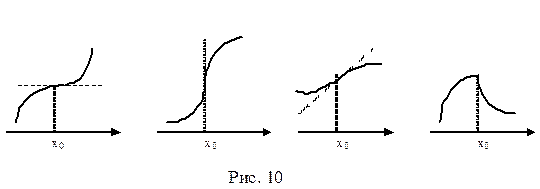 |
Теорема 7. (Критерий перегиба)Пусть функция f непрерывна в некоторой окрестности U  точки х0 ,
точки х0 ,  , и дифференцируема в проколотой окрестности
, и дифференцируема в проколотой окрестности  . Для того, чтобы х0 была точкой перегиба, необходимо и достаточно, чтобы существовало δ > 0 такое, что на одном из интервалов (х0 – δ , х0) и (х0 , х0 + δ) производная f ′ возрастает, а на другом – убывает.
. Для того, чтобы х0 была точкой перегиба, необходимо и достаточно, чтобы существовало δ > 0 такое, что на одном из интервалов (х0 – δ , х0) и (х0 , х0 + δ) производная f ′ возрастает, а на другом – убывает.
Утверждение этой теоремы вытекает непосредственно из критерия выпуклости ( теорема 6), так как в силу критерия интервалы строгой выпуклости функции совпадают с интервалами строгой монотонности её производной.
Следствие. Точка перегиба дифференцируемой функции является точкой строгого локального экстремума её производной.
Теорема 8.Пусть х0 , 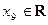 , является точкой перегиба функции f. Если f дважды дифференцируема в этой точке, то
, является точкой перегиба функции f. Если f дважды дифференцируема в этой точке, то 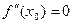 .
.
► В силу следствия предыдущей теоремы х0 является точкой строгого локального экстремума производной f ′. Так как f дважды дифференцируема в х0 , то f ′ дифференцируема в этой точке; значит, по теореме Ферма производная от f ′, т.е. 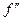 , в точке х0 обращается в 0 . ◄
, в точке х0 обращается в 0 . ◄
Следствие. Если f дважды дифференцируема в точке х0, а 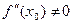 , то х0 заведомо не является точкой перегиба функции f.
, то х0 заведомо не является точкой перегиба функции f.
Пусть функция f непрерывна в точке х0 , 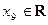 . Точку х0 будем называть точкой, подозрительной на перегиб, если либо
. Точку х0 будем называть точкой, подозрительной на перегиб, если либо 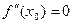 , либо
, либо 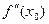 не существует. Из теоремы 8 и ее следствия вытекает, что только такие точки могут быть точками перегиба. Однако, не всегда точка, подозрительная на перегиб, на деле оказывается точкой перегиба.
не существует. Из теоремы 8 и ее следствия вытекает, что только такие точки могут быть точками перегиба. Однако, не всегда точка, подозрительная на перегиб, на деле оказывается точкой перегиба.
Пример 8. Пусть f(x) =x 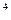 . Имеем:
. Имеем: 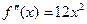 . Так как
. Так как 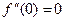 , то х0 = 0 – точка, подозрительная на перегиб. Однако,
, то х0 = 0 – точка, подозрительная на перегиб. Однако, 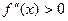 и на (- ∞, 0), и на (0, +∞); так что оба эти интервала являются интервалами выпуклости вниз.
и на (- ∞, 0), и на (0, +∞); так что оба эти интервала являются интервалами выпуклости вниз.
Теорема 9.(Достаточный признак перегиба) Пусть х0 , 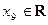 . есть точка, подозрительная на перегиб функции f , и пусть f дважды дифференцируема в проколотой окрестности этой точки.. Тогда
. есть точка, подозрительная на перегиб функции f , и пусть f дважды дифференцируема в проколотой окрестности этой точки.. Тогда
1)если 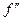 меняет знак при переходе через х0 , то х0 является точкой перегиба;
меняет знак при переходе через х0 , то х0 является точкой перегиба;
2)если 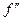 не меняет знак при переходе через х0 , то х0 не является точкой перегиба;
не меняет знак при переходе через х0 , то х0 не является точкой перегиба;
► 1) Пусть, например, 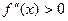 на (х0 – δ , х0) и
на (х0 – δ , х0) и 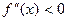 на (х0 , х0 + δ), где δ – некоторое положительное число. Так как
на (х0 , х0 + δ), где δ – некоторое положительное число. Так как 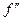 есть производная от
есть производная от 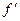 , в силу достаточного признака строгой монотонности
, в силу достаточного признака строгой монотонности 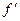 возрастает на первом интервале и убывает на втором. Значит (см. критерий выпуклости) первый интервал есть интервал строгой выпуклости вниз, а второй – строгой выпуклости вверх; поэтому х0 - точка перегиба.
возрастает на первом интервале и убывает на втором. Значит (см. критерий выпуклости) первый интервал есть интервал строгой выпуклости вниз, а второй – строгой выпуклости вверх; поэтому х0 - точка перегиба.
Доказательство утверждения 2) аналогично. ◄
Пример 9. Пусть f(x) =x 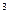 . Имеем:
. Имеем: 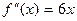 ,
, 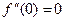 . Следовательно, х0 = 0 есть точка, подозрительная на перегиб, и так как при переходе через х0
. Следовательно, х0 = 0 есть точка, подозрительная на перегиб, и так как при переходе через х0 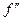 меняет знак, то х0 = 0 – точка перегиба.
меняет знак, то х0 = 0 – точка перегиба.
Пример 10. Пусть f(x) =x 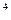 . Имеем:
. Имеем: 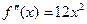 . Так как
. Так как 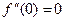 , то х0 = 0 – точка, подозрительная на перегиб. Но при переходе через х0 = 0 знак
, то х0 = 0 – точка, подозрительная на перегиб. Но при переходе через х0 = 0 знак 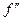 не меняется; значит, х0 = 0 точкой перегиба не является.
не меняется; значит, х0 = 0 точкой перегиба не является.
3.5. Асимптоты функции
Пусть 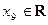 , а функция f определена в проколотой окрестности
, а функция f определена в проколотой окрестности 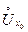
Определение 1. Если 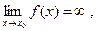 то прямую х = х0 назовем вертикальной асимптотой функции f при х→х0 .
то прямую х = х0 назовем вертикальной асимптотой функции f при х→х0 .
Пусть функция f определена в односторонней окрестности 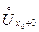 =(х0, х0 + δ) (
=(х0, х0 + δ) ( 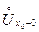 = (х0 – δ , х0) ), где δ – некоторое положительное число.
= (х0 – δ , х0) ), где δ – некоторое положительное число.
Определение 2. Если 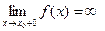 (
( 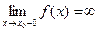 ), то прямую х = х0 назовем вертикальной асимптотой функции f при х→х0 + 0 (при х→х0 - 0 ).
), то прямую х = х0 назовем вертикальной асимптотой функции f при х→х0 + 0 (при х→х0 - 0 ).
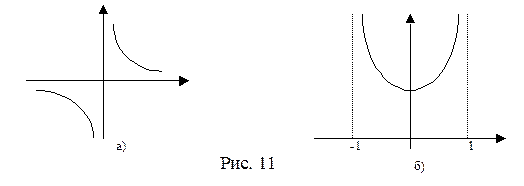
На рис. 11а) изображен график функции 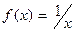 . Так как её предел при х→ 0 равен ∞, то прямая х = 0 ( ось ординат ) является вертикальной асимптотой этой функции при х→ 0 . На рис. 11б) представлен график функции
. Так как её предел при х→ 0 равен ∞, то прямая х = 0 ( ось ординат ) является вертикальной асимптотой этой функции при х→ 0 . На рис. 11б) представлен график функции 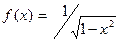 . Так как
. Так как 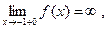
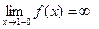 , то прямые х =-1 и х = 1 являются вертикальными асимптотами этой функции при х→ -1+0 и при х→ 1=0 соответственно.
, то прямые х =-1 и х = 1 являются вертикальными асимптотами этой функции при х→ -1+0 и при х→ 1=0 соответственно.
Пусть функция f определена на интервале (- ∞, а) или на интерва- ле (а, +∞) , где а – некоторое число. Пусть L – прямая, не параллельная оси OY , а y = kx + b – её уравнение.
Определение 3. Если 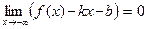 (
( 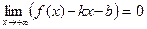 ) , то прямую L назовем наклонной асимптотой функции f при х→ - ∞ (при х→ +∞).
) , то прямую L назовем наклонной асимптотой функции f при х→ - ∞ (при х→ +∞).
Пример 11. Пусть a и b – положительные числа, 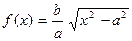 .Функция f определена этим равенством на интервалах (- ∞, - а) и (а, +∞), её график представлен на рис.11. Пусть L – прямая, уравнение которой
.Функция f определена этим равенством на интервалах (- ∞, - а) и (а, +∞), её график представлен на рис.11. Пусть L – прямая, уравнение которой 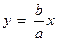 . Покажем, что L является наклонной асимптотой функции f при х→ + ∞. Действительно,
. Покажем, что L является наклонной асимптотой функции f при х→ + ∞. Действительно, 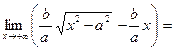 .
. 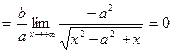
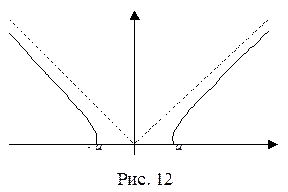 Аналогично можно показать, что пря-мая
Аналогично можно показать, что пря-мая 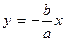 является наклонной асимптотой функции f при х→ - ∞.
является наклонной асимптотой функции f при х→ - ∞.
Теорема 10. (О наклонной асимпто- те)Пусть функция f определена на интервале (- ∞, а) . 1) Для того, чтобы существовала её наклонная асимптота при х→ - ∞, необходимо и достаточно, чтобы существовали пределы
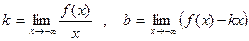 . (16) 2) Если пределы (16) существуют, то прямая, уравнение которой y = kx + +b есть наклонная асимптота функции f при х→ - ∞.
. (16) 2) Если пределы (16) существуют, то прямая, уравнение которой y = kx + +b есть наклонная асимптота функции f при х→ - ∞.
► 1) Необходимость. Пусть наклонная асимптота функции f при х→ - ∞ существует, а y = kx + b – её уравнение : 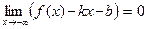 . Обозначим:
. Обозначим: 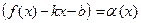 . Тогда
. Тогда 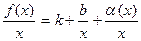 , и так как
, и так как 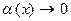 при х→ - ∞, то
при х→ - ∞, то 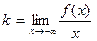 , т.е. первый из пределов (16) существует. Из равенства
, т.е. первый из пределов (16) существует. Из равенства 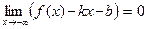 и теоремы о разности между функцией и числом ([1] , стр. 50) следует:
и теоремы о разности между функцией и числом ([1] , стр. 50) следует: 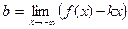 , т.е. второй из пределов (16) также существует.
, т.е. второй из пределов (16) также существует.
Достаточность. Пусть 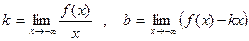 , а L – пря- мая, уравнение которой y = kx + b. Из равенства
, а L – пря- мая, уравнение которой y = kx + b. Из равенства 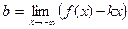 и теоремы о разности между функцией и числом следует:
и теоремы о разности между функцией и числом следует: 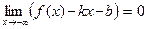 , а это означает, что L является асимптотой при х→ - ∞.
, а это означает, что L является асимптотой при х→ - ∞.
2) Это утверждение уже доказано, см. 1) , Достаточность. ◄
Теорема 11.Пусть функция f определена на интервале (а , + ∞) .
1) Для того, чтобы существовала её наклонная асимптота при х→ + ∞, необходимо и достаточно, чтобы существовали пределы
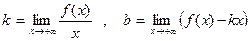 .
.
2) Если эти пределы существуют, то прямая, уравнение которой y = kx + +b есть наклонная асимптота функции f при х→ + ∞.
Доказательство теоремы аналогично приведенному выше.
3.6. Исследование функции, заданной параметрическим способом
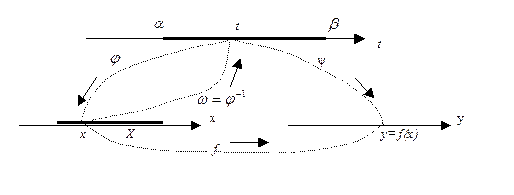
Пусть на некотором промежутке 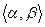 ,
, 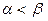 , определены функции
, определены функции 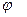 и
и 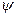 .
.
Рис. 13
Множество значений функции 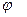 на
на 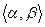 обозначим через Х Пусть
обозначим через Х Пусть 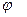 взаимно однозначно отображает
взаимно однозначно отображает 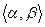 на Х ( заметим, что это требование будет выполнено, если
на Х ( заметим, что это требование будет выполнено, если 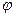 строго монотонна на
строго монотонна на 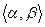 ). Значит, существует обратная функция
). Значит, существует обратная функция 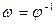 , которая определена на Х и взаимно однозначно отбражает Х на
, которая определена на Х и взаимно однозначно отбражает Х на 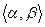 (гл.1, п.5.5). Тогда можно рассматривать функцию у = f(х) , заданную на множестве Х равенством f(х) =
(гл.1, п.5.5). Тогда можно рассматривать функцию у = f(х) , заданную на множестве Х равенством f(х) = 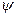
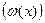 .
.
Таким образом, если каждая из двух переменных х и у является функцией некоторой третьей переменной t ( 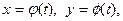 причём
причём 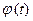 строго монотонна ), то переменные х и у связаны функциональной зависимостью: у = f(х). Говорят, что указанную зависимость можно задать параметрическим способом посредством системы
строго монотонна ), то переменные х и у связаны функциональной зависимостью: у = f(х). Говорят, что указанную зависимость можно задать параметрическим способом посредством системы
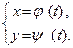
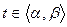 . (17)
. (17)
Саму систему (17) называют параметрическим представлением функции f(х) на множестве Х ; переменную t называют при этом параметром . Чтобы получить явное задание у = f(х) , следует из первого уравнения системы (17) найти t: t = 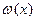 , а результат подставить во второе уравнение: у =
, а результат подставить во второе уравнение: у = 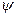 (
( 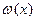 ) = f(x).
) = f(x).
Пример 12. Рассмотрим систему
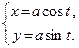
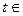 [0, π], где a>0. Функция
[0, π], где a>0. Функция 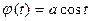 строго монотонна на [0, π], она взаимно однозначно отображает [0, π] на множество её Х = [-а, а]; поэтому система является параметрическим представлением некоторой функции y = f(x) на множестве Х = [-а, а]. Чтобы получить явное задание этой функции, найти f(x), найдем t из первого уравнения: t = = arccos
строго монотонна на [0, π], она взаимно однозначно отображает [0, π] на множество её Х = [-а, а]; поэтому система является параметрическим представлением некоторой функции y = f(x) на множестве Х = [-а, а]. Чтобы получить явное задание этой функции, найти f(x), найдем t из первого уравнения: t = = arccos 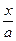 =
= 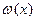 ; подставив результат во второе уравнение, получим:
; подставив результат во второе уравнение, получим:
y = f(x) = a sin( arccos 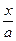 ) =
) = 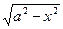 .
.
Пример 13. Рассмотрим систему
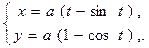
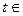 [0, 2π]. (18)
[0, 2π]. (18)
Имеем: 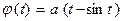 ,
, 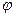 ′
′ 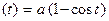 > 0 на (0, 2π); значит,
> 0 на (0, 2π); значит, 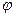 возрастает на [0, 2π] от 0 до 2πа. Поэтому рассматриваемая система является параметрическим представлением некоторой функции y = f (x), область определения которой есть сегмент [0, 2π а]. Чтобы найти f (x), нужна обратная функция
возрастает на [0, 2π] от 0 до 2πа. Поэтому рассматриваемая система является параметрическим представлением некоторой функции y = f (x), область определения которой есть сегмент [0, 2π а]. Чтобы найти f (x), нужна обратная функция 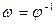 . Для её отыскания следует разрешить уравнение
. Для её отыскания следует разрешить уравнение 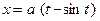 относительно t . Ясно, однако, что сделать это не удастся, следовательно, не удастся получить явное задание для f(x).
относительно t . Ясно, однако, что сделать это не удастся, следовательно, не удастся получить явное задание для f(x).
Параметрический способ задания функции – один из наиболее распространенных, в том числе и в приложениях математики. Как свидетельствует пример 13, для функции, заданной таким способом, не всегда удается получить её явное задание вида y = f(x). В таких случаях возникает задача: пусть известно параметрическое представление (17) функции f , т.е. известны функции 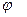 и
и 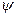 ; можно ли, обладая только информацией о свойствах
; можно ли, обладая только информацией о свойствах 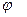 и
и 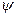 , выяснить основные свойства функции f : непрерывна ли она? дифференцируема ли? как найти её производную? Ниже даны ответы на эти вопросы.
, выяснить основные свойства функции f : непрерывна ли она? дифференцируема ли? как найти её производную? Ниже даны ответы на эти вопросы.
1. Если 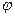 и
и 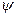 непрерывны на (
непрерывны на ( 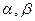 ), то f непрерывна на интервале (a,b) – множестве значений функции
), то f непрерывна на интервале (a,b) – множестве значений функции 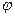 на (
на ( 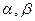 ).
).
Действительно, по теореме о множестве значений строго монотонной функции (гл. 1,п 5.4 ), множество значений функции 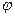 на (
на ( 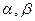 ) есть некоторый интервал; обозначим его через (a,b). По теореме о непрерывности обратной функции (гл.1, п. 5.5 ) функция
) есть некоторый интервал; обозначим его через (a,b). По теореме о непрерывности обратной функции (гл.1, п. 5.5 ) функция 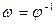 непрерывна на (a,b). По теореме о непрерывности сложной функции (гл. 1, п.5.2) суперпозиция непрерывных функций
непрерывна на (a,b). По теореме о непрерывности сложной функции (гл. 1, п.5.2) суперпозиция непрерывных функций 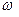 и
и 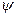 , т.е., функция f , непрерывна на (a,b).
, т.е., функция f , непрерывна на (a,b).
2. Если 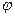 и
и 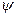 дифференцируемы на (
дифференцируемы на ( 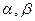 ), причем производная
), причем производная 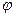 ′ (t) не обращается в нуль на (
′ (t) не обращается в нуль на ( 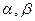 ),то f дифференцируема на (a,b), а для её производной f ′ справедливо параметрическое представление
),то f дифференцируема на (a,b), а для её производной f ′ справедливо параметрическое представление
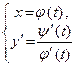 t
t 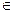 (
( 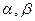 ). (19)
). (19)
В самом деле, по теореме о производной обратной функции ( п.1.3, теорема 5) функция 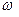 дифференцируема в каждой точке интервала (a,b), причем
дифференцируема в каждой точке интервала (a,b), причем 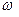 ′(х) = =
′(х) = = 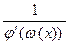 . По теореме о производной сложной функции ( п.1.3, теорема 4) функция
. По теореме о производной сложной функции ( п.1.3, теорема 4) функция 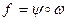 дифференцируема в каждой точке интервала (a,b), причем
дифференцируема в каждой точке интервала (a,b), причем
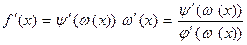 . . Обозначим:
. . Обозначим: 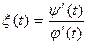 , и рассмотрим систему
, и рассмотрим систему 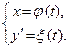 t
t 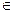 (
( 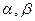 ). Так как
). Так как 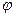 - строго монотонная функция, то эта система является параметрическим представлением функции y′=
- строго монотонная функция, то эта система является параметрическим представлением функции y′= 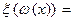
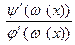 , т.е. функции f ′.
, т.е. функции f ′.
3. Если 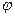 и
и 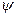 дважды дифференцируемы на (
дважды дифференцируемы на ( 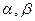 ), причем производная
), причем производная 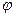 ′ (t) не обращается в нуль на (
′ (t) не обращается в нуль на ( 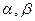 ),то f дважды дифференцируема на (a,b), а для её производной f ″ справедливо параметрическое представление
),то f дважды дифференцируема на (a,b), а для её производной f ″ справедливо параметрическое представление
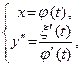 t
t 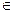 (
( 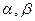 ), где
), где 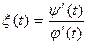 . Обосновать эти утверждения можно так же, как утверждения 2, рассмотрев систему (19) как параметрическое представление функции f ′.
. Обосновать эти утверждения можно так же, как утверждения 2, рассмотрев систему (19) как параметрическое представление функции f ′.
Пример 14. Пусть f – функция, параметрическим представлением которой является система (18). Областью её определения является сегмент [0, 2π а] (см. пример 13). Непосредственно из 1. следует: f непрерывна на (0, 2π а). Этот вывод можно дополнить: f непрерывна на сегменте [0, 2π а]. Действительно, 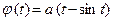 возрастает и непрерывна на сегменте [0, 2π], значит, обратная функция
возрастает и непрерывна на сегменте [0, 2π], значит, обратная функция 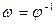 возрастает и непрерывна также на сегменте [0, 2π а] ([1], см. замечание к теореме 1); поэтому и f непрерывна на этом сегменте. Непосредственно из 2. и 3. следует: f дважды дифференцируема на (0, 2π а), а для её производных справедливы параметрические представления
возрастает и непрерывна также на сегменте [0, 2π а] ([1], см. замечание к теореме 1); поэтому и f непрерывна на этом сегменте. Непосредственно из 2. и 3. следует: f дважды дифференцируема на (0, 2π а), а для её производных справедливы параметрические представления
f ′: 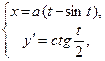 t
t 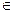 (0, 2π) ; f ″ :
(0, 2π) ; f ″ : 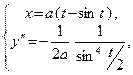 t
t 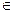 (0, 2π) ;
(0, 2π) ;
Основываясь на этих сведениях о функции f и её производных можно изучить поведение функции и построить её график. При t 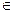 (0, π) x =a(t – sint) принадлежит (0, аπ ), y =a (1 – cost) принадлежит (0,2а), a
(0, π) x =a(t – sint) принадлежит (0, аπ ), y =a (1 – cost) принадлежит (0,2а), a 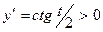 . Значит, f ′ (x)> 0 на интервале (0, аπ); поэтому f возрастает на сегменте [0, аπ] от нуля до 2а. Рассмотрев t
. Значит, f ′ (x)> 0 на интервале (0, аπ); поэтому f возрастает на сегменте [0, аπ] от нуля до 2а. Рассмотрев t 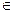 (π , 2π) так же можно установить,что на сегменте [аπ, 2π а ] f убывает от 2а до нуля, следовательно, х0 = аπ есть точка строгого максимума функции f , причем f (аπ) = 2а. При всех t
(π , 2π) так же можно установить,что на сегменте [аπ, 2π а ] f убывает от 2а до нуля, следовательно, х0 = аπ есть точка строгого максимума функции f , причем f (аπ) = 2а. При всех t 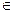 (0, 2π)
(0, 2π)
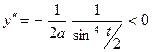 ,
,
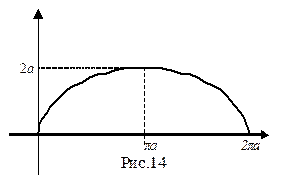
значит, f ″ (х) < 0 при всех 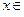 (0,2а), поэтому f строго выпукла вверх на сегменте [0, 2π а]
(0,2а), поэтому f строго выпукла вверх на сегменте [0, 2π а]
