Уравнение Пуассона в прямоугольнике
Первая краевая задача. В области 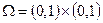 с границей
с границей 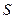 рассмотрим краевую задачу
рассмотрим краевую задачу
 , (3.1)
, (3.1)
 . (3.2)
. (3.2)
Такая задача возникает, например, при отыскании положения равновесия тонкой упругой однородной мембраны, закрепленной на границе и находящейся под воздействием внешней силы 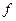 . Потенциальная энергия этой мембраны задается интегралом
. Потенциальная энергия этой мембраны задается интегралом
 , (3.3)
, (3.3)
где
 .
.
Согласно принципу Гамильтона, равновесное положение мембраны достигается для функции, реализующей минимум функционала (3.3) на множестве допустимых функций – это эквивалентная формулировка краевой задачи (3.1), (3.2). Множество допустимых функций образует пространство  , которое вводится так же, как и в одномерном случае:
, которое вводится так же, как и в одномерном случае:  это пространство функций, имеющих первые производные и удовлетворяющих краевому условию (3.2). Норма в
это пространство функций, имеющих первые производные и удовлетворяющих краевому условию (3.2). Норма в  определяется так:
определяется так:
 .
.
Введем пространство  пространство функций, имеющих производные первого и второго порядка и удовлетворяющих условию (3.2). Норма в этом пространстве определяется так:
пространство функций, имеющих производные первого и второго порядка и удовлетворяющих условию (3.2). Норма в этом пространстве определяется так:
 .
.
Как и в одномерном случае, можно показать, что решение задачи (3.1), (3.2) доставляет минимум функционалу (3.3). Верно и обратное: функция из  , доставляющая минимум функционалу (3.3), является решением задачи (3.1), (3.2). Вычисляя вариацию функционала (3.3) и приравнивая ее нулю, получим условие минимума функционала (3.3) в виде
, доставляющая минимум функционалу (3.3), является решением задачи (3.1), (3.2). Вычисляя вариацию функционала (3.3) и приравнивая ее нулю, получим условие минимума функционала (3.3) в виде
 ,
,
где  произвольная функция из
произвольная функция из  .
.
Рассмотрим билинейную форму
 ,
,  ,
,
определенную на функциях из  . Тогда условие минимума можно переписать в виде
. Тогда условие минимума можно переписать в виде
 . (3.4)
. (3.4)
Равенство (3.4) можно рассматривать как уравнение для нахождения решения краевой задачи (3.1), (3.2) в обобщенной постановке.
Именно обобщенным решением задачи (3.1), (3.2) из пространства  называют функцию, удовлетворяющую (3.4) при произвольной функции
называют функцию, удовлетворяющую (3.4) при произвольной функции 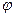 из пространства
из пространства  .
.
Для того, чтобы решение задачи (3.1), (3.2) принадлежало  , правая часть
, правая часть 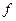 должна принадлежать пространству
должна принадлежать пространству  , т.е. иметь конечную норму:
, т.е. иметь конечную норму:
 .
.
Для существования обобщенного решения достаточно, чтобы для любых функций  был ограничен интеграл
был ограничен интеграл
 .
.
Легко решается вопрос о единственности обобщенного решения задачи (3.1), (3.2). Для этого используется неравенство
 . (3.5)
. (3.5)
Это неравенство доказывается аналогично неравенству (1.22). Если неравенство (3.5) доказано, то дальнейшее просто. Пусть у задачи (3.1), (3.2) имеется два обобщенных решения  и
и  . Тогда, согласно (3.4):
. Тогда, согласно (3.4):
 .
.
Следовательно, в силу (3.5)  .
.
Вторая краевая задача. Вторую краевую задачу рассмотрим не для уравнения Пуассона, а для чуть более общего уравнения
 ,
,  , (3.6)
, (3.6)
 , (3.7)
, (3.7)
где 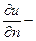 производная по направлению внешней нормали к
производная по направлению внешней нормали к  .
.
Уравнение (3.6) является уравнением Эйлера для функционала
 . (3.8)
. (3.8)
Решение задачи (3.6), (3.7) доставляет минимум функционалу (3.8) на множестве допустимых функций, представляющих собой пространство функций  . Верно и обратное: функция из
. Верно и обратное: функция из  , доставляющая минимум (3.8), является решением задачи (3.6), (3.7). Доказывается это точно так же, как в одномерном случае.
, доставляющая минимум (3.8), является решением задачи (3.6), (3.7). Доказывается это точно так же, как в одномерном случае.
Вычислим вариацию функционала (3.8) и приравняем ее нулю.
Получим
 ,
,
где  произвольная функция из
произвольная функция из  . Это условие минимума функционала (3.8).
. Это условие минимума функционала (3.8).
Введем в рассмотрение билинейную форму
 ,
,  ,
,
определенную на функциях из  , и перепишем условие минимума в виде
, и перепишем условие минимума в виде
 (3.9)
(3.9)
Обобщенное решение задачи (3.6), (3.7) определяется как функция из  , удовлетворяющая (3.9) при произвольной функции
, удовлетворяющая (3.9) при произвольной функции 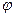 из
из  .
.
Здесь следует обратить внимание на то, что как задача минимизации функционала (3.8), так и задача по определению обобщенного решения находятся на множестве функций, ''свободных'' на границе. Это связано с тем, что краевое условие (3.7) естественное. Последнее означает, что функция из  , удовлетворяющая (3.9) или доставляющая минимум функционалу (3.8), уже в силу самого этого факта удовлетворяет краевому условию (3.7). В этом нетрудно убедиться, проведя интегрирование по частям в (3.9).
, удовлетворяющая (3.9) или доставляющая минимум функционалу (3.8), уже в силу самого этого факта удовлетворяет краевому условию (3.7). В этом нетрудно убедиться, проведя интегрирование по частям в (3.9).
Для задачи (3.6), (3.7) также имеет место единственность обобщенного решения.
Можно показать, что билинейные формы являются скалярными произведениями в пространствах  и
и  соответственно. С помощью этих скалярных произведений вводятся энергетические нормы
соответственно. С помощью этих скалярных произведений вводятся энергетические нормы
|| 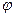 ||
||  ,
,  ,
,
|| 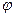 ||
||  ,
,  .
.
