Задачи для самостоятельного решения. 1.Построить ряд распределения и функцию распределения случайного числа попаданий
1.Построить ряд распределения и функцию распределения случайного числа попаданий мячом в корзину при одном броске, если вероятность попадания мячом в корзину при одном броске p=0,3.
2.Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения числа попаданий (Воспользоваться формулой Бернулли).
3.В урне имеются четыре шара с номерами от 1 до 4. Вынули два шара. Случайная величина X – сумма номеров шаров. Построить ряд распределения величины X.
4.Контрольная работа состоит из трех вопросов. На каждый вопрос приведено 4 ответа, один из которых правильный. Составить закон распределения числа правильных ответов при простом угадывании. Найти математическое ожидание и дисперсию этой случайной величины.
5.В билете три задачи. Вероятность правильного решения первой задачи равна 0,9, второй – 0,8, третьей – 0,7. Составить закон распределения числа правильно решенных задач в билете и вычислить математическое ожидание и дисперсию этой случайной величины.
6.В партии, содержащей 20 изделий, имеется четыре изделия с дефектами. Наудачу отобрали три изделия для проверки их качества. Составить закон (ряд) распределения случайной величины X – числа дефектных изделий, содержащихся в указанной выборке. Найти математическое ожидание, дисперсию, моду случайной величины X.
7.Найти закон распределения числа пакетов трех акций, по которым владельцем будет получен доход, если вероятность получения дохода по каждому из них равна соответственно 0,5, 0,6, 0,7. Найти математическое ожидание, дисперсию и моду данной случайной величины, построить функцию распределения.
8.Дана функция распределения случайной величины X
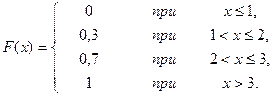
Найти: а) ряд распределения; б) M(X) и D(X); в) построить многоугольник распределения и график F(x).
9. Случайная величина 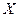 имеет следующую функцию распределения F(x):
имеет следующую функцию распределения F(x):
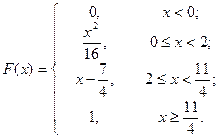
Требуется: а) найти плотность вероятностей 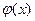 случайной величины
случайной величины 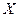 ; б) построить графики F(x) и
; б) построить графики F(x) и 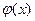 ; в) определить математическое ожидание, дисперсию и среднее квадратическое отклонение величины
; в) определить математическое ожидание, дисперсию и среднее квадратическое отклонение величины 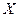 ; г) найти вероятность попадания случайной величины
; г) найти вероятность попадания случайной величины 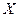 на отрезок [1; 1,5].
на отрезок [1; 1,5].
10. Функция распределения случайной величины 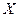 имеет вид
имеет вид
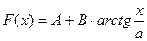 (
( 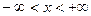 ) (закон Коши).
) (закон Коши).
Определить постоянные A и B, найти плотность вероятностей 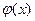 .
.
11. Дана функция 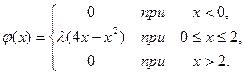
При каком значении 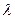 функция
функция 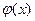 может быть принята за плотность вероятности случайной величины X? Определить это значение
может быть принята за плотность вероятности случайной величины X? Определить это значение 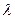 , найти математическое ожидание и среднее квадратическое отклонение соответствующей случайной величины X.
, найти математическое ожидание и среднее квадратическое отклонение соответствующей случайной величины X.
12. Случайная величина 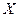 имеет следующую плотность вероятностей:
имеет следующую плотность вероятностей:
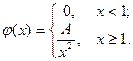
Определить: а) коэффициент A; б) функцию распределения F(x); в) вероятность 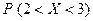 попадания случайной величины
попадания случайной величины 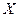 в интервал (2; 3); г) вероятность того, что при четырех независимых испытаниях величина
в интервал (2; 3); г) вероятность того, что при четырех независимых испытаниях величина 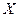 ни разу не попадает в интервал (2; 3).
ни разу не попадает в интервал (2; 3).
13. Случайная величина X задана функцией распределения
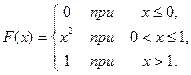
Найти: а) плотность вероятности 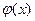 ; б) M(X) и D(X); в) вероятности P(X = 0,5), P(X<0,5), P(
; б) M(X) и D(X); в) вероятности P(X = 0,5), P(X<0,5), P( 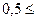 X
X 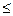 1); г) построить графики
1); г) построить графики 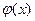 и F(x).
и F(x).
14. Функция распределения непрерывной случайной величины X задана
следующим образом:
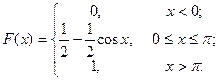
Требуется: а) найти плотность вероятностей 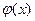 величины X; б) построить графики F(x) и
величины X; б) построить графики F(x) и 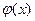 ; в) найти
; в) найти 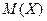 ,
, 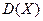 и
и 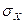 ; г) определить вероятность попадания случайной величины X в интервал
; г) определить вероятность попадания случайной величины X в интервал 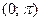 .
.
15. Случайная величина X распределена по закону Коши: 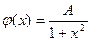 . Найти: а) коэффициент A; б) функцию распределения F(x); в) вероятность P(
. Найти: а) коэффициент A; б) функцию распределения F(x); в) вероятность P( 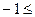 X
X 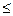 1). Существует ли для случайной величины X математическое ожидание и дисперсия?
1). Существует ли для случайной величины X математическое ожидание и дисперсия?
16. Дана функция распределения случайной величины X:
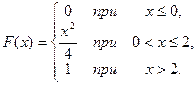
а) Найти плотность вероятности 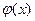 ; построить графики
; построить графики 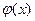 и F(x); убедиться в том, что X – непрерывная случайная величина; б) Найти вероятности P(X=1), P(X<1), P(1
и F(x); убедиться в том, что X – непрерывная случайная величина; б) Найти вероятности P(X=1), P(X<1), P(1 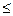 X
X 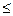 2); в) вычислить математическое ожидание M(X), дисперсию D(X), моду
2); в) вычислить математическое ожидание M(X), дисперсию D(X), моду 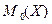 и медиану
и медиану 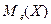 .
.
17. Скорость молекул газа имеет плотность вероятности (закон Максвелла)
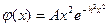 (
( 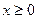 ).
).
Найти математическое ожидание и дисперсию скорости молекул, а также величину A при заданном h.
18. Дана плотность распределения непрерывной случайной величины:
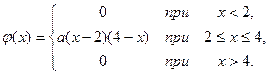
Определить значение 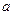 , моду и медиану.
, моду и медиану.
19. Случайная величина X задана функцией распределения
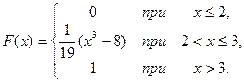
Найти математическое ожидание M(X), моду 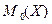 и медиану
и медиану 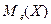 .
.
20. Случайная величина X задана плотностью вероятности 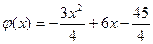 на интервале
на интервале 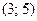 . Вне этого интервала
. Вне этого интервала 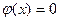 . Найти моду, медиану и математическое ожидание.
. Найти моду, медиану и математическое ожидание.
