Определение длины кривой. Дифференциал кривой
Если кривая y=f(x) на отрезке [a; b] - гладкая (т. е. производная y’=f’(x) непрерывна), то длина соответствующей дуги этой кривой находится по формуле:
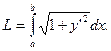
При параметрическом задании кривой x=x(t), y=y(t) [x(t) и y(t) – непрерывно дифференцируемые функции] длина дуги кривой, соответствующая монотонному изменению параметра t от t1 до t2, вычисляется по формуле:
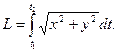
Если гладкая кривая задана в полярных системах координатах уравнением ρ=ρ(θ), α ≤ θ ≤ β, то длина дуги равна:
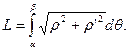
Дифференциал длины дуги. Длина дуги кривой определяется формулой:
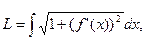
где y=f(x) 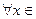 [a; b]. Предположим, что в этой формуле нижний передел интегрирования остается постоянным, а верхний изменяется. Обозначим верхний предел буквой х, а переменную интегрирования буквой t. Длина дуги будет функцией верхнего предела:
[a; b]. Предположим, что в этой формуле нижний передел интегрирования остается постоянным, а верхний изменяется. Обозначим верхний предел буквой х, а переменную интегрирования буквой t. Длина дуги будет функцией верхнего предела:
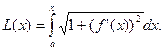
Первая теорема Гульдена
Пусть криволинейная трапеция вращается вокруг оси oX. Тогда она опишет тело вращения с массой 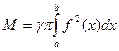 .
.
Из формулы для центра масс знаем: 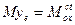
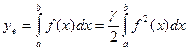
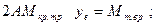
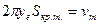
Объем тела, полученного вращением криволинейной трапеции, равен произведению площади этой трапеции на длину окружности, описанную из центра масс.
Вторая теорема Гульдена
Пусть плоская дуга вращается вокруг оси oX. Она опишет площадь: 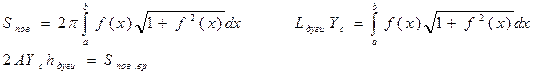
Площадь поверхности, полученная вращением дуги, равна произведению длины этой дуги на длину окружности, описывающую центр масс.
Несобственные интегралы
Для существования определенного интеграла должны выполняться два условия:
1. Предел интегрирования конечный;
2. Подынтегральная функция ограничена.
Нарушение этих двух условий приводит к несуществующему интегралу.
В этом случае вводится обобщение определенного интеграла, который называется несобственным интегралом.
1. Несобственный интеграл с бесконечным пределом интегрирования.
а) 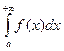 - Пусть
- Пусть 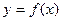 - интегрируема на любом
- интегрируема на любом 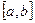 , где
, где 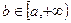 , то по определению:
, то по определению: 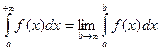
Если предел в правой части существует и конечен, говорят, что, интеграл сходится; нет - расходится.
б) 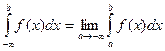
в) 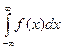 Этот случай сводится к предыдущему.
Этот случай сводится к предыдущему.
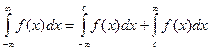 ,
, 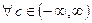 ; Результат от с не зависит.
; Результат от с не зависит.
Интеграл в левой части существует, если интеграл в правой части существует по отдельности, т.е. пределы интегрирования в этих интегралах надо обозначать разными буквами.
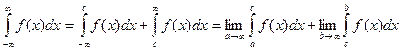
Признаки сходимости
В некоторых случаях достаточно знать, сходится интеграл или нет, без его вычисления. Для этого применяется признак сравнения.
1). Пусть 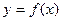 и
и 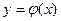 интегрируемы на
интегрируемы на 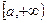 и удовлетворяют на этом промежутке неравенству:
и удовлетворяют на этом промежутке неравенству: 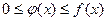 , то справедливо следующее утверждение:
, то справедливо следующее утверждение:
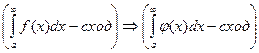 ;
; 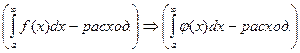
Обратное утверждение неверно!!!
Раздел 5. Обыкновенные дифференциальные уравнения
