Справочный материал к заданию. Скалярное произведение векторов

Скалярное произведение векторов

Скалярным произведение двух векторов и называется число
· = ( , ), равное произведению модулей (длин) этих векторов на косинус угла между ними:

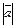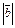· = ( , ) = · · cos ( , ^ )

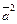Скалярное произведение · называется скалярным квадратом вектора и обозначается . Из определения скалярного произведения следует, что 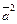= 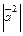и = = .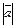

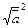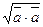Угол между векторами и вычисляется по формуле

.

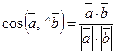Основные свойства скалярного произведения

.

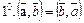
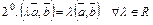
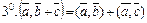
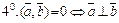Геометрический смысл скалярного произведения

Скалярное произведение векторов можно выразить через проекцию одного вектора-сомножителя на другой по формуле:

( , ) = · = .

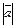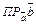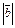
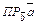Если векторы и заданы своими координатами:

= {a_x, a_y, a_z}, = {b_x, b_y, b_z},

то:

· = a_x · b_x + a_y · b_y + a_z · b_z;

= ;

.

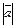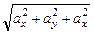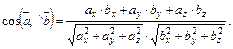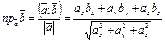
Векторное произведение векторов

Векторным произведением вектора на вектор называется вектор × 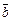= [ , ], определяемый тремя условиями:

1) модуль вектора × равен: 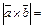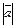· · 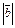sin ( , ^ );

2) вектор × перпендикулярен к каждому из векторов и ;

3) векторы , и × , взятые в указанном порядке, образуют правую тройку, т.е. из конца вектора × кратчайший поворот от вектора к вектору виден совершающимся против часовой стрелки.

Основные свойства векторного произведения

. .

. || .

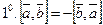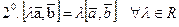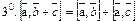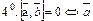Геометрический смысл векторного произведения

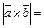
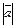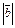Модуль векторного произведения векторов и равен площади параллелограмма, построенного на векторах и как на сторонах: · · sin( , ^ ).

Если векторы и заданы своими координатами: = {a_x, a_y, a_z},
= {b_x, b_y, b_z}, то векторное произведение × определяется формулой:

× =

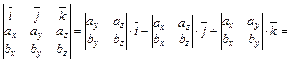
= (a_yb_z – b_ya_z) 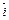– (a_xb_z –a_zb_x) 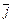+ (a_xb_y – b_xa_y) .

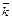Длина высоты параллелограмма, построенного на векторах и , опущенной на основание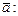

Смешанное произведение трех векторов

Смешанным произведением трех векторов , и 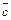называется число ( , , 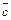), равное векторному произведению [ , ], умноженному скалярно на вектор . ( , , ) = ( × ) · .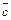

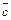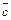Основные свойства смешанного произведения

1⁰. Смешанное произведение векторов не меняется при циклической перестановке его сомножителей: ( , , )=( , , )= ( , , ).

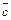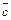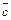2⁰. Если тройка , , 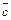правая, то ( , , 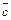) > 0; если тройка , , 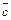левая, то ( , , 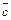) < 0.

3⁰. , , 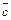компланарны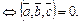

Геометрический смысл смешанного произведения

Модуль смешанного произведения векторов , , 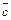равен объему параллепипеда, построенного на векторах , , 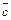как на сторонах.

Если векторы , , 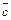заданы своими координатами: = {a_x, a_y, a_z}, = 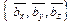, 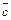= 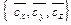, то смешанное произведение
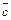( , , ) определяется формулой:

( , , ) =

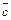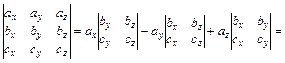
= a_x(b_yc_z – c_yb_z) – a_y(b_xc_z – b_zc_x) + a_z(b_xc_y – c_xb_y).

Плоскость в пространстве

Любой ненулевой вектор 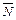, перпендикулярный к данной плоскости П, называется ее нормальным вектором.

В декартовых координатах каждая плоскость П определяется уравнением первой степени, и каждое уравнение первой степени определяет плоскость. Общее уравнение плоскости:

Ах + By + Cz + D = 0, (1)

при этом вектор 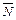= {A, B, C} является нормальным вектором этой плоскости, .

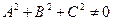Уравнение плоскости, проходящий через точку М₀ (x₀, y₀, z₀) перпендикулярно вектору 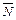= {A, B, C}:

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0.

Уравнение плоскости в отрезках:

,

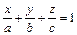где а, b, c — абcцисса, ордината и аппликата соответственно точек пересечения плоскости с координатными осями.

Уравнение плоскости, проходящей через три точки М₁(x₁, y₁, z₁),
М₂(x₂, y₂, z₂), М₃(x₃, y₃, z₃):

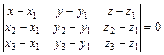. (2)

Уравнение плоскости, проходящей через две точки М₁(x₁, y₁, z₁)
и М₂(x₂, y₂, z₂) перпендикулярно к плоскости A(x – x₀)+B(y – y₀) + C(z – z₀) = 0:

.

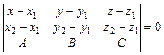Уравнение плоскости, проходящей через точку М₀(x₀, y₀, z₀) перпендикулярно к двум непараллельным плоскостям A₁x+B₁y+C₁z+ D₁ = 0 и A₂x + B₂y + C₂z + D₂ 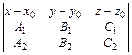= 0:

= 0.

Расстояние от точки М(x^*, y^*, z^*) до плоскости Ах + By + Cz + D = 0 вычисляется по формуле:

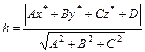. (3)

Прямая в пространстве

Ненулевой вектор , параллельный прямой l, называется направляющим вектором этой прямой.

Канонические уравнения прямой, проходящей через данную точку М₀(x₀, y₀, z₀) с заданным направляющим вектором = {m, n, p}:

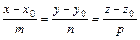. (4)

Уравнения прямой, проходящей через две данные точки
М₁(x₁, y₁, z₁) и М₂(x₂, y₂, z₂):

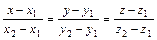. (5)

Углы между прямой и плоскостью, между двумя прямыми

Углом 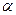между прямой l и плоскостью П называется угол
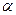(0 £ 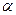£ 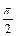), образованный прямой l и ее проекцией l¢ на эту плоскость.

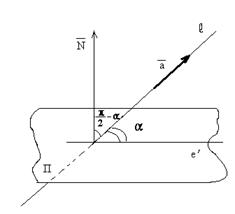
Зная нормальный вектор 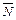= {A, B, C} плоскости П и направляющий вектор = {m, n, p} прямой l, угол j можно определить из формулы:

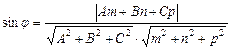. (6)

Угол между двумя прямыми в пространстве – это угол между направляющими векторами этих прямых.