Теория вероятностей. Математическая статистика

17.2.1. Х – число выпадения герба при двух бросаниях монеты. Найти дисперсию случайной величины Х.

17.2.2. Х – число выпадения надписи при двух бросаниях монеты. Найти дисперсию случайной величины Х.

17.2.3. В урне находится 2 белых и 3 черных шара. Наудачу извлекается 2 шара. Х – число белых шаров среди отобранных. Найти дисперсию случайной величины Х.

17.2.4. Х – число выпадений пятерки на игральной кости. Найти дисперсию случайной величины Х.

17.2.5. Вероятность того, что прибор исправен равна 0,8. Х – число исправных приборов из двух выбранных. Найти дисперсию случайной величины Х.

17.2.6. В коробке 5 кубиков пронумерованных от 1 до 5. Мальчик произвольным образом вынимает 2 кубика. Х – число кубиков с нечетным номером среди двух выбранных. Найти дисперсию случайной величины Х.

17.2.7. Станок-автомат производит 90% изделий первого сорта, 7% второго, а остальные третьего. Х – число изделий первого сорта среди двух выбранных. Найти дисперсию случайной величины Х.

17.2.8. Вероятность того, что в пакетике с чипсами попадется призовой купон равна 0,1. Х – число пакетиков с купонами среди двух выбранных. Найти дисперсию случайной величины Х.

17.2.9. В группе из шести человек два отличника. Наугад выбрали двух человек. Х – число отличников из выбранных. Найти дисперсию случайной величины Х.

17.2.10. 5% лотерейных билетов – выигрышные. Х – число выигрышных билетов среди двух выбранных. Найти дисперсию случайной величины Х.

17.2.31–17.2.40.Дискретная случайная величина X может принимать только два значения: х₁ и х₂ причем х₁ < х₂. Известны вероятность р₁возможного значения х математическое ожидание М(Х) и дис­персия D(X). Найти закон распределения этой случайной величины.

17.2.31. р₁= 0,1; М(Х)=3,9; D(X)=0,09.

17.2.32. р₁= 0,3; М(Х)=3,7; D(X)=0,21.

17.2.33. р₁=0,5; М(Х)=3,5; D(X)=0,25.

17.2.34. р₁=0,7; М(Х)=3,3; D(X)=0,21.

17.2.35. р₁=0,9; М(Х)=3,1; D(X)=0,09.

17.2.36. р₁=0,9; М(Х)=2,2; D(X)=0,36.

17.2.37. р₁=0,8; М(Х)=3,2; D(X)=0,16.

17.2.38. р₁=0,6; М(Х)=3,4; D(X)=0,24.

17.2.39. р₁=0,4; М(Х)=3,6; D(X)=0,24.

17.2.40. р₁=0,2; М(Х)=3,8; D(X)=0,16.

17.2.41–17.2.50.Случайная величина X задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. Схематично построить графики функций F(x) и f(x).

17.2.41.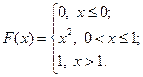

17.2.42.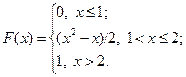

17.2.43.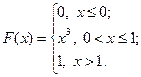

17.2.44.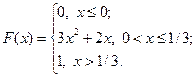

17.2.45.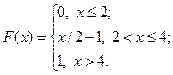

17.2.46.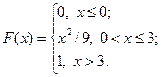

17.2.47.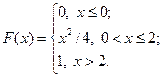

17.2.48.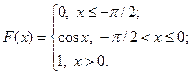

17.2.49.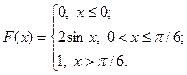

17.2.50.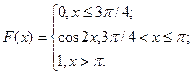

17.3.11–17.3.20.Нормально распределенная случайная величина Х задана своими параметрами а (математическое ожидание) и s (среднее квадратическое отклонение). Требуется:

а) написать плотность вероятности и схематически изобразить ее график;

б) найти вероятность того, что Х примет значение из интервала (a; b);

в) найти вероятность того, что Х отклонится (по модулю) от а не более чем на d;

г) применяя правило “трех сигм” найти границы интервала, содержащего соответствующие значения случайной величины Х .

17.3.11. а = 7, s = 2, a = 6, b = 10, d = 3.

17.3.12. a = 6, s = 1, a = 4, b = 7, d = 1.

17.3.13. a = 5, s = 3, a = 1, b = 6, d = 2.

17.3.14. a = 4, s = 2, a = 5, b = 6, d = 4.

17.3.15. a = 3, s = 1, a = 4, b = 6, d = 2.

17.3.16. a = 2, s = 1, a = 1, b = 3, d = 2.

17.3.17. a = 10, s = 4, a = 5, b = 12, d = 2.

17.3.18. a = 9, s = 5, a = 4, b = 12, d = 2,5.

17.3.19. a = 8, s = 2, a = 5, b = 10, d = 3.

17.3.20. a = 7, s = 3, a = 4, b = 8, d = 2.

19.1.11–19.1.20.Найти доверительный интервал для оценки математического ожидания а нормального распределения с надежностью 0,95, зная выборочную среднюю 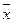, объем выборки n и среднее квадратическое отклонение σ.

19.1.11. 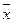= 75,17, n = 36, σ = 6.

19.1.12. 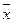=75,16, n = 49, σ = 7.

19.1.13. 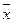= 75,15, n = 64, σ = 8.

19.1.14. 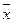= 75,14, n = 81, σ = 9.

19.1.15. 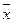= 75,13, n = 100 , σ =10.

19.1.16. 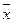= 75,12, n = 12I, σ =11.

19.1.17. 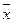= 75,11, n = 144, σ =12 .

19.1.18. 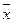= 75,10, n = 169, σ =13.

19.1.19. 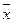= 75,09, n =196, σ =14.

19.1.20. 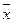= 75,08, n = 225, σ =15.

19.3.1–19.3.10.Известно эмпирическое распределение выборки объема n случайной величины Х. Проверить гипотезу о распределении по закону Пуассона генеральной совокупности этой величины. Использовать критерий согласия Пирсона (хи-квадрат) при уровне значимости 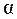= 0,05.

Номер	хi							n
19.3.1	ni
19.3.2	ni
19.3.3	ni
19.3.4	ni
19.3.5	ni
19.3.6	ni
19.3.7	ni
19.3.8	ni
19.3.9	ni
19.3.10	ni