Свойства неопределенного интеграла.

Таблица основных интегралов

Пользуясь определением первообразной функции, можно доказать следующие свойства неопределенного интеграла.

1) Производная от неопределенного интеграла равна подынтегральной функции:

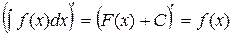
2) Дифференциал от неопределенного интеграла равен подынтегральному выражению: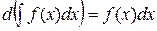

Действительно, используя формулу du = u¢(x)dx и первое свойство, получим

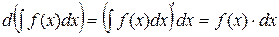
3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная: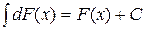

Действительно, так как dF(x) = F¢(x)dx, то 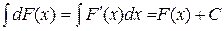, т.к. F(x)– есть первообразная для F ¢(x).

4) Константу можно выносить за знак неопределенного интеграла : .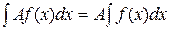

Действительно, 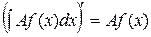по свойству первому, и

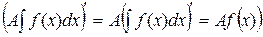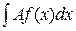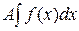. Значит, и есть первообразные одной и той же функции Аf(x), поэтому, по теореме 1.1, они равны между собой с точностью до константы.

5) Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от слагаемых в отдельности: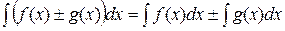

Пусть 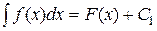, а 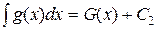. Тогда 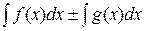= (F(x) +C₁) ± (G(x) +C₂) = (F(x) ± G(x))+(C₁ ± C₂) = (F(x) ± G(x))+C = 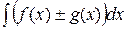– ч.т.д.

Заметим, что это свойство можно распространить на сумму любого конечного числа слагаемых. Свойства 4 и 5 можно объединить в одно, называемое свойством линейности неопределенного интеграла

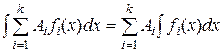
6) Если 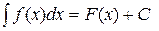, то для любой дифференцируемой функции и = и(х) имеет место равенство 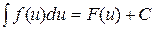. Это свойство называется свойством инвариантности неопределенного интеграла.

Докажем его. По условию, F(x) есть первообразная для f(x), т.е. F ¢(x) = f(x). Пусть и = и(х) любая дифференцируемая функция. Тогда

f(u)du = f(u(x))du(x) = f(u(x))u¢(x)dx.

Доказать свойство 6 – значит, доказать, что F(u) = F(u(x)) есть первообразная для функции f(u(x))u¢(x). Но это действительно так, поскольку по правилу дифференцирования сложной функции имеем

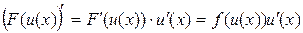
Значит, 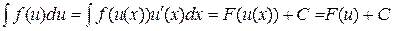. Ч.т.д.

В частности, из этого свойства следует, что

, ,

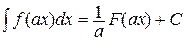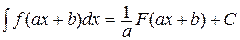Поскольку операция интегрирования является обратной операции дифференцирования, то каждой из ранее доказанных формул дифференцирования соответствует обратная ей формула интегрирования. Составим таблицу, в которой каждой формуле дифференцирования поставим в соответствие обратную ей формулу интегрирования (будем полагать, как обычно, что х – независимая переменная, а>0, a ÎR и СÎR – константы):

1. С¢ = 0	1.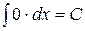
2. х¢ = 1	2.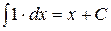
3.	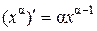3.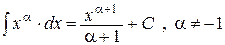
4.	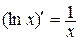4.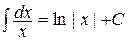
5. (ах)¢ = ахlna	5.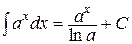
6. (ex)¢ = ex	6.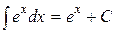
7. (cosx)¢ = – sinx	7.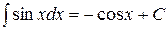
8. (sinx)¢ = cosx	8.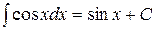
9.	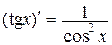9.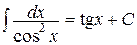
10.	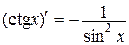10.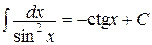
11. 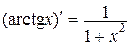,	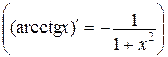11.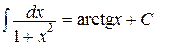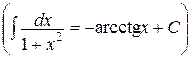
12. 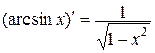,	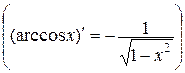12.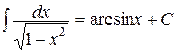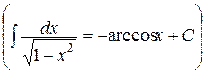

Для удобства вычислений дополним таблицу еще несколькими часто встречающимися интегралами:

13.

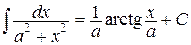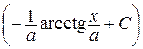14.

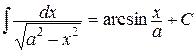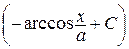15.

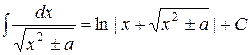16.

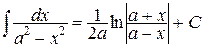Рассмотрим примеры использования свойств интегралов и табличных формул.

Пример1.

а)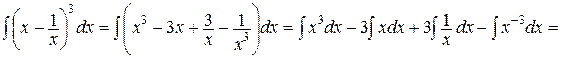

.

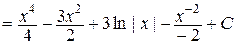б)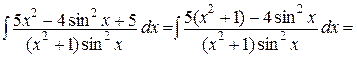

.
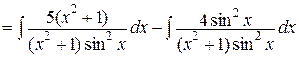