Моделирование гидродинамических процессов
Рассмотрим подобие стационарного течения несжимаемой вязкой жидкости для следующих случаев:
– при наличии влияния веса;
– при отсутствии влияния веса;
– вязкостное и инерционное течение.
Последние три вида течения являются частными случаями первого.
Течение при наличии влияния веса.
Дифференциальные уравнения движения
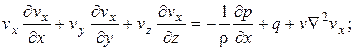
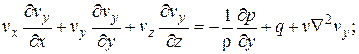 (4.76)
(4.76)
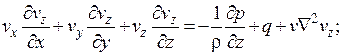
уравнение сплошности
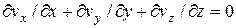 . (4.77)
. (4.77)
Уравнения движения (4.76) и сплошности (4.77) могут быть записаны в векторной форме:
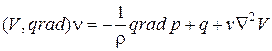 (4.78)
(4.78)
уравнение сплошности
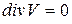 , (4.79)
, (4.79)
где V – вектор скорости;
v – скалярная величина того же вектора;
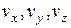 – проекции вектора V на координатные оси
– проекции вектора V на координатные оси 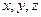 (причем х направлена вертикально);
(причем х направлена вертикально);
р – давление, отсчитанное от давления в некоторой точке потока, как от нуля;
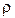 – плотность жидкости;
– плотность жидкости;
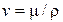 – коэффициент кинематической вязкости жидкости;
– коэффициент кинематической вязкости жидкости;
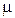 – коэффициент вязкости жидкости;
– коэффициент вязкости жидкости;
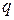 – ускорение свободного падения;
– ускорение свободного падения;
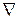 – оператор Лапласа.
– оператор Лапласа.
Величины 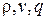 – рассматриваются как постоянные во всем поле.
– рассматриваются как постоянные во всем поле.
Краевые условия в рассматриваемой задаче не могут содержать никаких других физических переменных, кроме скорости, которая может быть задана на границе в виде уравнения, выражающего скорость как функцию координат точек границы. Если рассматривают течение жидкости внутри какого-либо аппарата, то границами потока следует считать входное сечение потока, где имеют место управляемые краевые условия, и поверхности твердых стенок, окаймляющих поток, где имеют место неуправляемые граничные условия (в случае неподвижных стенок v=0. Поскольку это условие автоматически соблюдается и в модели, и в образце, то задание краевых условий сводится к заданию скорости на входном сечении изучаемого объекта. Это заключение можно отнести и ко всем задачам, разбираемым в дальнейшем.
Так как в рассматриваемой задаче размерность скорости может быть представлена как
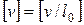 или
или 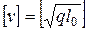 ,
,
то граничные условия могут быть записаны в виде:
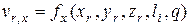 ;
;
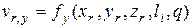 ; (4.80)
; (4.80)
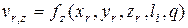 .
.
или
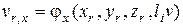 ;
;
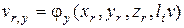 ; (4.81)
; (4.81)
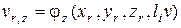 .
.
Как показали исследования, оба способа записи краевых условий приводит к одному и тому же конечному результату.
Для приведения уравнений (4.76), (4.77), (4.80) и (4.81) к безразмерному виду напишем масштабные преобразования:
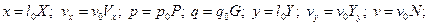
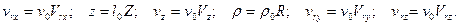
После введения преобразований в уравнения (4.76) и (4.77) получаем:
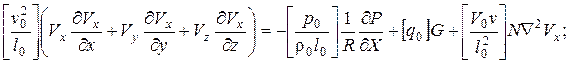
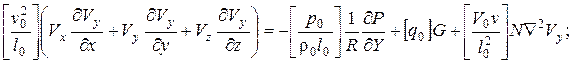
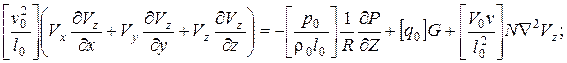
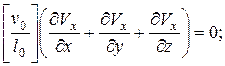
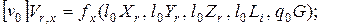
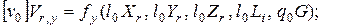
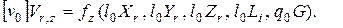
Для приведения этих уравнений к безразмерному виду необходимо, чтобы
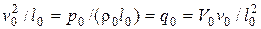 (4.86)
(4.86)
Из условий (4.86) можно получить три уравнения связи, которые содержат шесть масштабов. Следовательно, любые три из них, имеющие независимые размерности, можно выбрать в качестве основных, например, 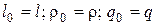 , а три остальных определить из уравнения связи (4.86).
, а три остальных определить из уравнения связи (4.86).
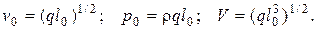
Тогда выражения для безразмерных величин можно записать:
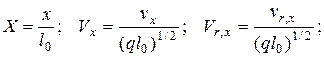
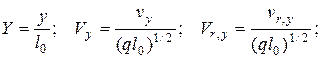
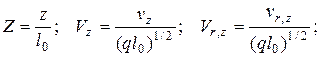
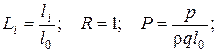
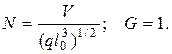 (4.87)
(4.87)
или
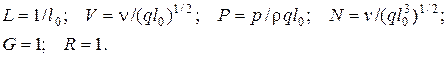 (4.88)
(4.88)
где 1 – радиус вектора;
L – безразмерный радиус-вектор какой-либо точки в потоке;
G – единичный вектор.
Уравнение движения:
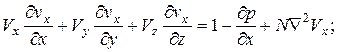
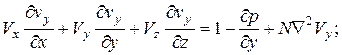 (4.89)
(4.89)
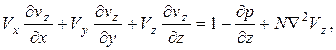
или в векторной форме
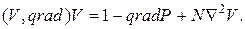 (4.90)
(4.90)
Уравнение сплошности
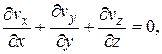 (4.91)
(4.91)
или в векторной форме 
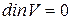 (4.92)
(4.92)
Граничные условия
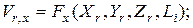
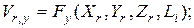

 (4.93)
(4.93)
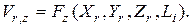
Решение системы дифференциальных уравнений (4.89) и (4.91), удовлетворяющей граничным условиям (4.93), можно представить в виде:
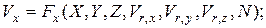

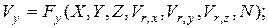
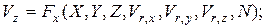
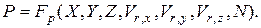 (4.94)
(4.94)
Следовательно, для соблюдения подобия двух потоков необходимо и достаточно осуществить равенство безразмерной скорости на границе потока в модели и образца и равенство критерия N в сравниваемых потоках, т.е. (в векторной форме)
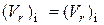 и
и 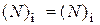 ,
,
или
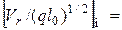
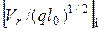 и
и 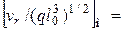
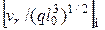 . (4.95)
. (4.95)
Если эти условия будут соблюдены, то в сходственных точках модели и образца, т.е. при
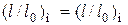
будут иметь место равенства:
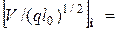
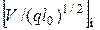 и
и 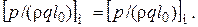
Интересно заметить, что имеющие широкое применение критерии 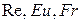 могут быть представлены как степенные функции критериев
могут быть представлены как степенные функции критериев 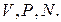 Действительно, воспользовавшись равенством (198), можно получить
Действительно, воспользовавшись равенством (198), можно получить
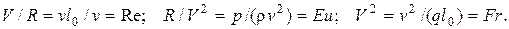
Из условий (4.95) видно, что осуществление требования 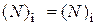 при условии, что жидкость в модели и образце одна и та же, т.е.
при условии, что жидкость в модели и образце одна и та же, т.е. 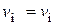 , возможно только при
, возможно только при 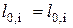 , т.е. когда размеры модели и образца одинаковы. В этом случае для выполнения условий
, т.е. когда размеры модели и образца одинаковы. В этом случае для выполнения условий 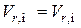 должно иметь равенство
должно иметь равенство 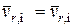 .
.
Установление вида функций 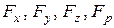 в большинстве практических задач осуществляется опытным путем. Однако экспериментальное определение указанных функций связано с большими трудностями (вести измерения скоростей и давлений в значительном количестве точек). Поэтому для практических задач нередко переходят на средние значения скорости и давления и устанавливают равенство ускоренных по сечению критериев давления
в большинстве практических задач осуществляется опытным путем. Однако экспериментальное определение указанных функций связано с большими трудностями (вести измерения скоростей и давлений в значительном количестве точек). Поэтому для практических задач нередко переходят на средние значения скорости и давления и устанавливают равенство ускоренных по сечению критериев давления 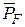 и скорости
и скорости 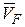 .
.
Перейдя к замене критериев 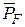 ,
, 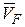 и N критериями
и N критериями 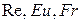 , было установлено на основании многочисленных экспериментальных исследований, что функциональная связь между критериями
, было установлено на основании многочисленных экспериментальных исследований, что функциональная связь между критериями 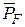 ,
, 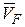 и N может быть представлена в виде
и N может быть представлена в виде
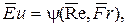 (4.96)
(4.96)
где
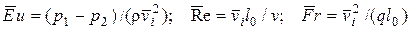 .
.
В гидравлике для подсчета сопротивления, возникающего вследствие трения при движении жидкости в канале или трубе, обычно пользуются формулой Дарси:
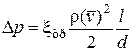 ,
,
а при определении местных сопротивлений – формулой Вейсбаха:
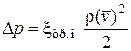 ,
,
где 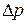 – падение напора между двумя сечениями;
– падение напора между двумя сечениями;
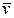 – средняя по сечению трубы скорость;
– средняя по сечению трубы скорость;
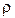 – плотность жидкости;
– плотность жидкости;
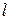 – длина трубы;
– длина трубы;
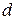 – гидравлический диаметр.
– гидравлический диаметр.
На сопоставление приведенных формул с выражением для критерия 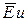 можно заключить, что
можно заключить, что
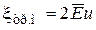 ;
;
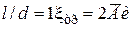 ,
,
т.е. коэффициенты сопротивления 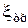 и
и 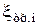 в общем случае в соответствии с выражением (4.96) являются функции критериев
в общем случае в соответствии с выражением (4.96) являются функции критериев 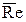 и
и 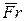 .
.
Течение при отсутствии влияния весахарактеризуется отсутствием свободных поверхностей, т.е. имеет место напорное течение. В этом случае влиянием веса можно пренебречь по сравнению с влиянием остальных сил, действующих на элементарную частицу жидкости.
На основании анализа дифференциальных уравнений:
движения
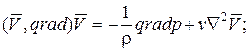
сплошности
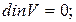
граничных условий
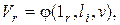
где 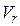 – вектор скорости в точках, расположенных на границах потока;
– вектор скорости в точках, расположенных на границах потока;
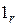 – радиус-вектор этих точек,
– радиус-вектор этих точек,
можно получить систему уравнений связи
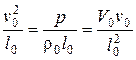 , (4.97)
, (4.97)
Используя уравнения связи, можно показать. так же как это было сделано при рассмотрении предыдущей задачи. что для осуществления подобия нужно на границах модели осуществить распределение критерия 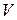 ,тождественно одинаковое с тем, которое имеет место в образце, т.е. выполнить условие
,тождественно одинаковое с тем, которое имеет место в образце, т.е. выполнить условие
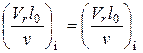 .
.
Переходя к усредненным по сечению критериям 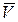 и
и 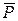 и заменяя их критериями
и заменяя их критериями 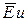 и
и 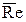 , результаты опытов, имеющих целью установление эмпирических законов сопротивления при напорном течении, обычно обрабатывается в виде функциональной зависимости
, результаты опытов, имеющих целью установление эмпирических законов сопротивления при напорном течении, обычно обрабатывается в виде функциональной зависимости
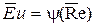 .
.
Вязкостный режим течения. Этот режим течения характеризуется исчезающе малым влиянием инерционных сил по сравнению с силами трения и давления. В этом случае на основании анализа уравнений:
движения
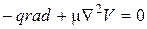 ;
;
сплошности
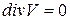 ;
;
граничных условий
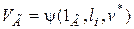 ,
,
где 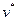 – параметрическое значение скорости,
– параметрическое значение скорости,
получается одно уравнение связи
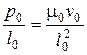 , (4.98)
, (4.98)
на основании которого, устанавливается подобие двух потоков.
Для осуществления подобия необходимо выполнить равенство критериев 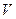 на границах потоков в модели и в образце, т.е.
на границах потоков в модели и в образце, т.е.
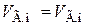 или
или 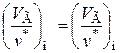 .
.
Отсюда видно, что подобие может быть осуществлено независимо от размеров модели.
Инерционный режим течения. В этом случае влиянием сил трения, ввиду их малости по сравнению с силами давления и инерции, на режим течения можно пренебречь.
Тогда после приведения уравнений:
движения
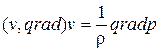 ;
;
сплошности
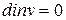 ;
;
граничных условий
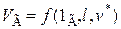
и безразмерному виду получим уравнение связи
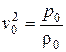 . (4.99)
. (4.99)
Следовательно, для установления подобия между двумя потоками необходимо выполнить то же условие, что и при вязкостном режиме, т.е.
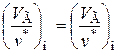 .
.
В данном случае подобие может быть осуществлено, так же как при вязкостном режиме, независимо от размеров модели, которая. разумеется, должна быть геометрически подобна образцу.
Сопоставим условия, необходимые для осуществления подобия в рассматриваемых задачах:
при наличии сил тяжести:
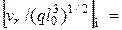
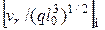 ;
;
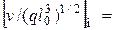
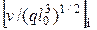 ;
;
при напорном течении
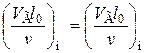 ;
;
при вязкостном течении
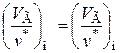 ;
;
при инерционном течении
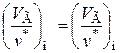 .
.
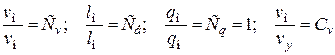 ,
,
получим при наличии влияния сил тяжести
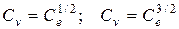 ;
;
при напорном течении
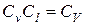 ;
;
при вязкостном и инерционном течении
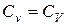 .
.
Следовательно, для первых двух режимов имеем ограничения в выборе множителей подобия. Действительно, выбрав в первом случае множитель геометрического подобия 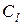 , мы тем самым предопределяем множители подобия
, мы тем самым предопределяем множители подобия 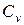 и
и 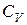 . Аналогично и в случае напорного течения.
. Аналогично и в случае напорного течения.
В противоположность рассмотренным двум первым видам течения, при осуществлении подобия вязкости и инерционного течения мы свободны в выборе множителей подобия. В последних двух случаях подобие обеспечивается одним лишь подобием распределения скоростей. Это свойство инерционного и вязкостного режимов течения называется автомоделью. При этом для вязкостного режима имеет место
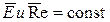 ,
,
а для инерционного режима
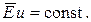
Вязкостный режим наблюдается в области малых значений числа 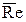 , а инерционный – в области больших значений числа
, а инерционный – в области больших значений числа 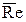 . В соответствии с этим принято говорить о первой и второй автомодельных областях. Значение автомодельности для практики моделирования совершенно очевидно, так как оно позволяет осуществить подобие на модели любых размеров с использованием любой рабочей жидкости.
. В соответствии с этим принято говорить о первой и второй автомодельных областях. Значение автомодельности для практики моделирования совершенно очевидно, так как оно позволяет осуществить подобие на модели любых размеров с использованием любой рабочей жидкости.
