Приклад 4. Метод Рунге–Кутта.

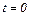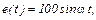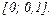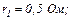
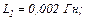
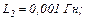
Обчислити методом Рунге–Кутта струми та напругу на ємності в електричному колі (рис. 2.1), яке в момент часу вмикається на ЕРС для інтервалу часу Параметри схеми: 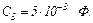До моменту комутації струм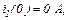 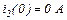та напруга на ємності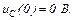

Розв’язання.

Крок інтегрування приймаємо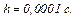

Запишемо на підставі законів Кірхгофа рівняння, які описують стан електричного кола, у нормальній формі Коші

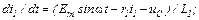
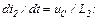
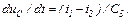
Алгоритм розрахунку такий:

– обчислюємо коефіцієнти приростів

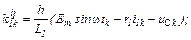
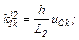
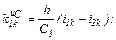
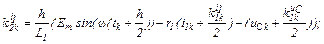
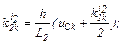
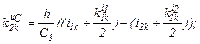
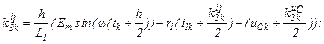
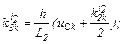
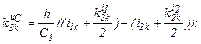
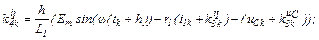
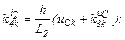
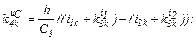
– обчислюємо прирости

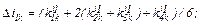
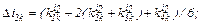
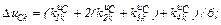
– знаходимо значення струмів віток та напругу на ємності

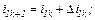
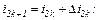
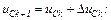
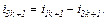
Перша ітерація.

обчислюємо коефіцієнти приростів

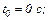
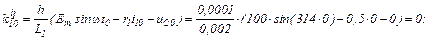
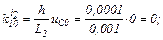
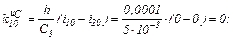
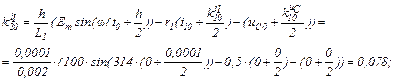
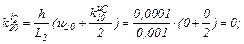
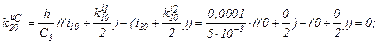
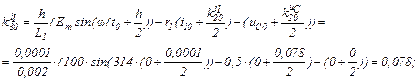
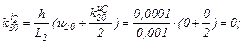
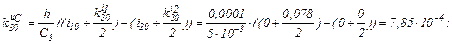
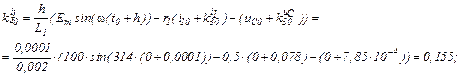
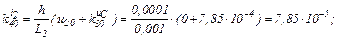
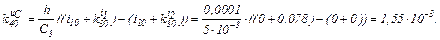
Визначаємо прирости

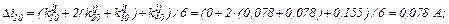
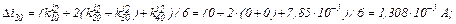
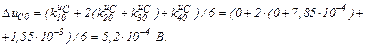
обчислюємо значення струмів віток та напругу на ємності

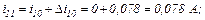
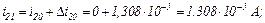
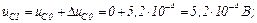
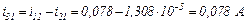
Друга ітерація.

Знаходимо коефіцієнти приростів

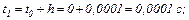
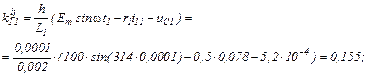
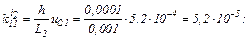
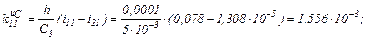
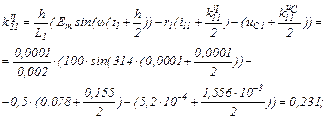
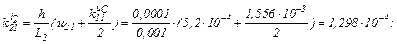
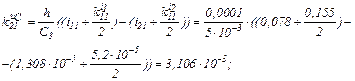
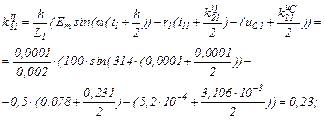
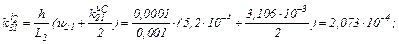
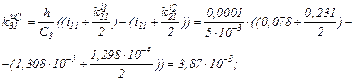
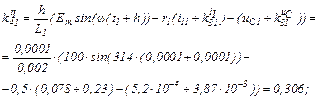
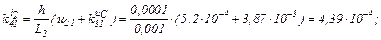
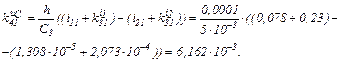
обчислюємо прирости

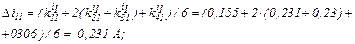
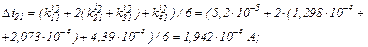
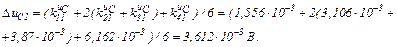
обчислюємо значення струмів віток та напругу на ємності

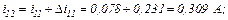
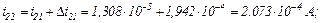
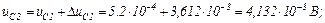
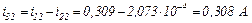
Третя ітерація.

Визначаємо коефіцієнти приростів

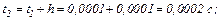
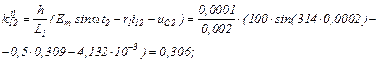
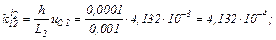
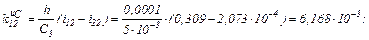
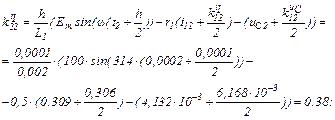
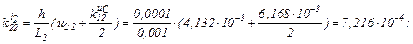
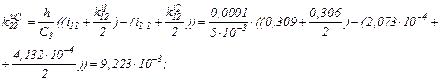
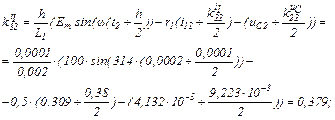
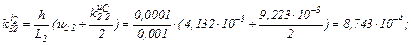
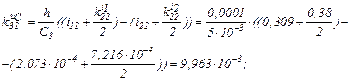
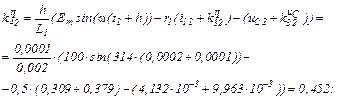
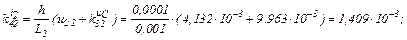
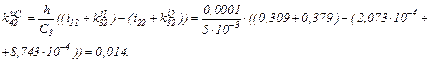
Розраховуємо прирости

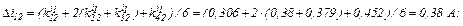
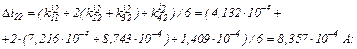
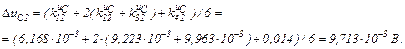
обчислюємо значення струмів віток та напругу на ємності

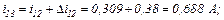
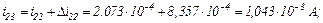
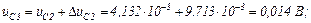
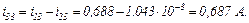
Використовуючи символьну математику MathCad, обчислюємо значення струмів у вітках електричного кола та напругу на ємності, залежності яких показані на рис. 2.8 та рис. 2.9 відповідно.

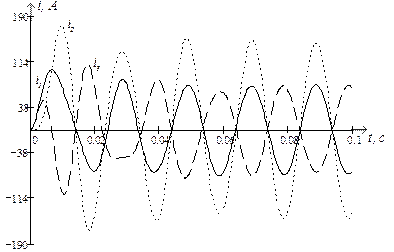
Рис. 2.8. Струми у вітках електричного кола під час вмикання

його на синусоїдну ЕРС

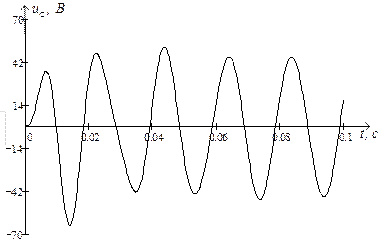
Рис. 2.9. Напруга на ємності ◄

Приклад 5. Метод Кутта–Мерсона.

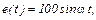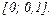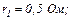
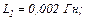
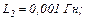
Обчислити методом Кутта–Мерсона струми та напругу на ємності в електрич­ному колі (рис. 2.1), яке в момент часу вмикається на ЕРС для інтервалу часу Параметри схеми: 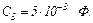До моменту комутації струм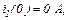 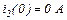та напруга на ємності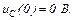

Розв’язання.

Крок інтегрування приймаємо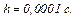

Запишемо на підставі законів Кірхгофа рівняння, які описують стан електричного кола, у нормальній формі Коші

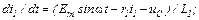
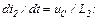
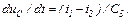
Алгоритм розрахунку такий:

– визначаємо коефіцієнти приростів

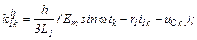
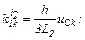
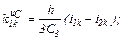
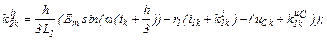
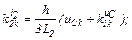
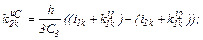
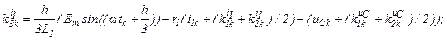
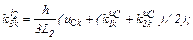
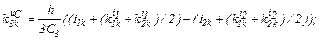
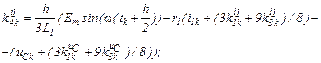
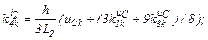
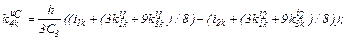
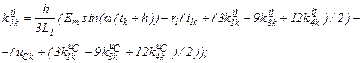
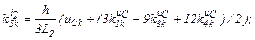
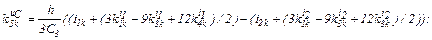
– обчислюємо струми віток та напругу на ємності

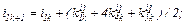
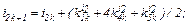
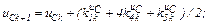
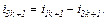
Перша ітерація.

Розраховуємо коефіцієнти приростів

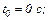
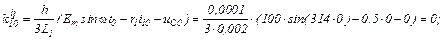
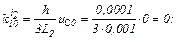
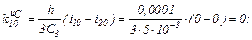
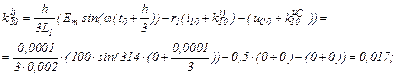
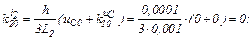
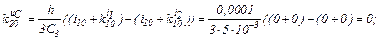
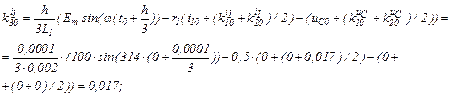
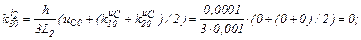
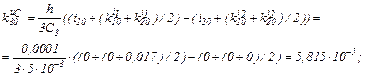
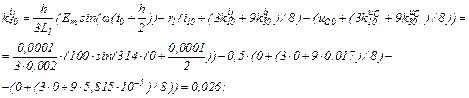
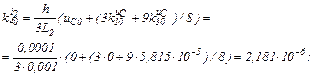
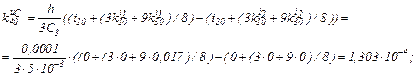
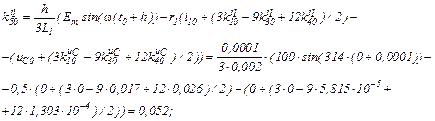
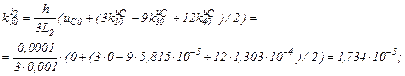
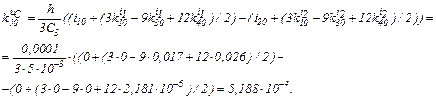
Обчислюємо струми віток та напругу на ємності

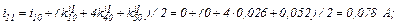
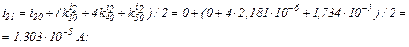
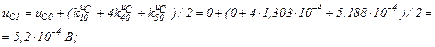
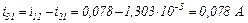
Друга ітерація.

Визначаємо коефіцієнти приростів

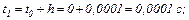
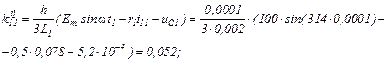
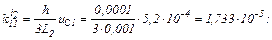
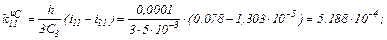
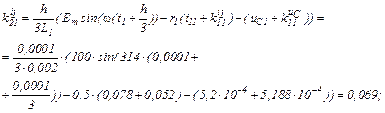
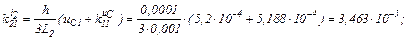
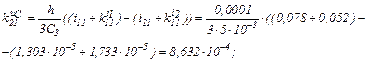
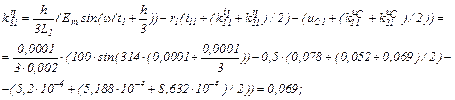
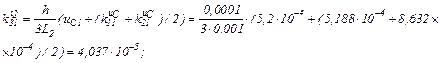
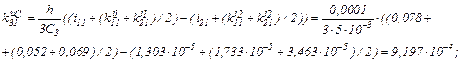
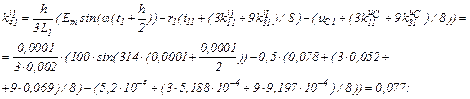
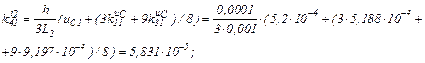
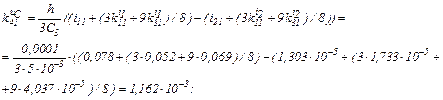
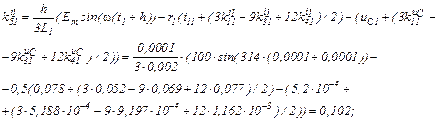
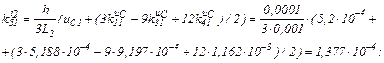
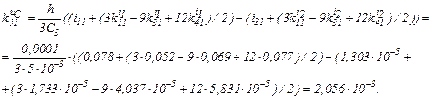
Знаходимо струми віток та напругу на ємності

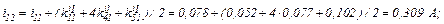
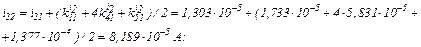
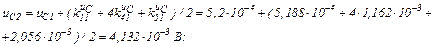
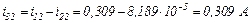
Третя ітерація.

обчислюємо коефіцієнти приростів

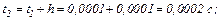
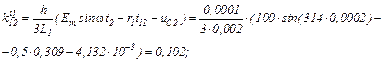
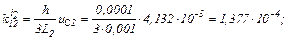
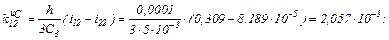
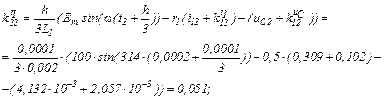
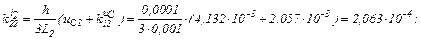
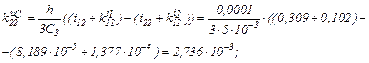
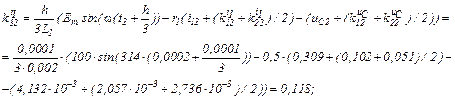
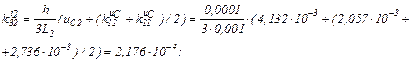
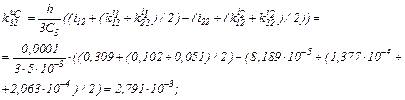
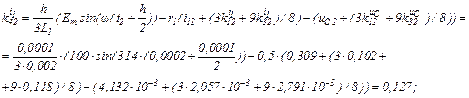
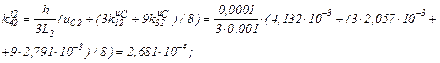
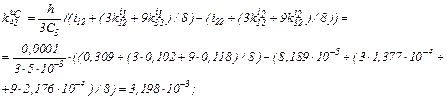
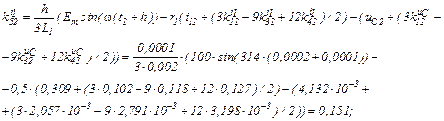
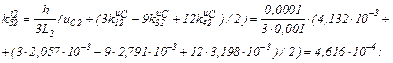
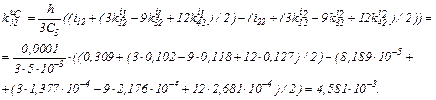
Визначаємо струми віток та напругу на ємності

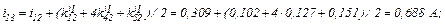
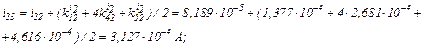
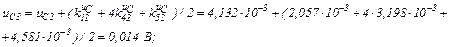
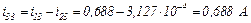
Використовуючи символьну математику MathCad, обчислюємо значення струмів у вітках електричного кола та напругу на ємності, залежності яких показані на рис. 2.10 та рис. 2.11 відповідно.

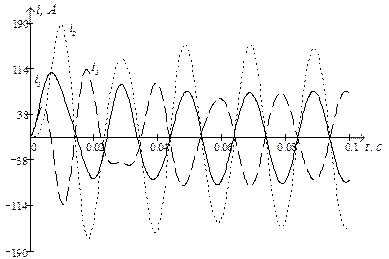
Рис. 2.10. Струми у вітках електричного кола під час вмикання

його на синусоїдну ЕРС

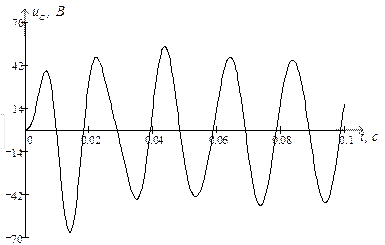
Рис. 2.11 Напруга на ємності ◄

Неявні методи

Приклад 6. Метод Ейлера.

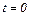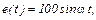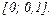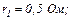
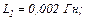
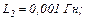
Обчислити неявним методом Ейлера струми та напругу на ємності в електрич­ному колі (рис. 2.1), яке в момент часу вмикається на ЕРС для інтервалу часу Параметри схеми: 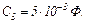До моменту комутації струм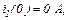 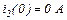та напруга на ємності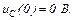

Розв’язання.

Крок інтегрування приймаємо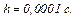

Точність обчислення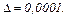

Записуємо рівняння, які описують стан електричного кола, у нормальній формі Коші

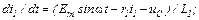
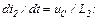
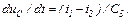
Для отриманої системи рівнянь обчислюємо матрицю Якобі

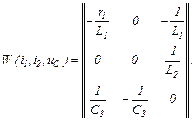
Нульове наближення на кожному ітераційному кроці обчислюємо на підставі явної форми Ейлера

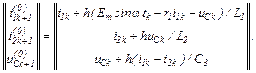
Робоча формула для -го кроку в 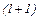-му ітераційному циклі

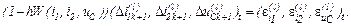
У розгорнутому вигляді

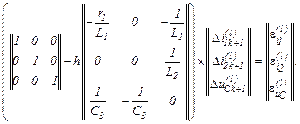
Алгоритм обчислення такий:

– обчислюємо вектор нев’язок

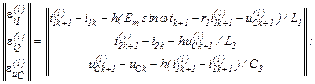
– визначаємо прирости

=

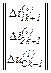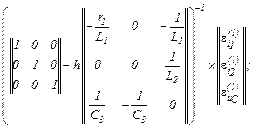
– знаходимо значення координат

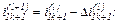
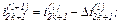
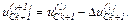
Якщо 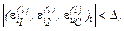тобто менше від заданої точності,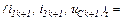 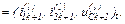В іншому разі ітераційний процес за вказаним алгоритмом продовжуємо до досягнення вказаної умови.

Перша ітерація.

Визначаємо нульове наближення на підставі явного методу Ейлера

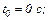
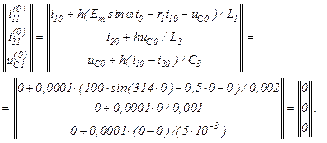
У розгорнутому вигляді система рівнянь має вигляд

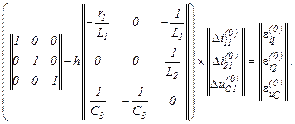
Обчислюємо в ітераційному циклі значення струмів віток та напруги на ємності на першому кроці за таким алгоритмом:

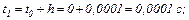
– вектор нев’язок

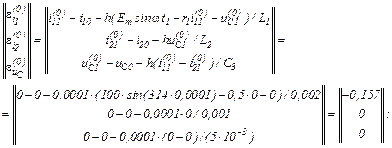
– обчислюємо прирости

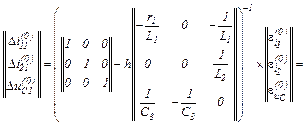
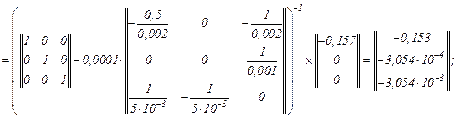
– значення струмів віток та напруги на ємності

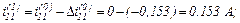
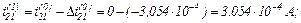
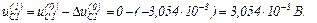
Оскільки 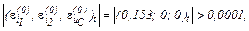продовжуємо ітераційний процес.

Другий крок в ітераційному циклі:

– визначаємо вектор нев’язок

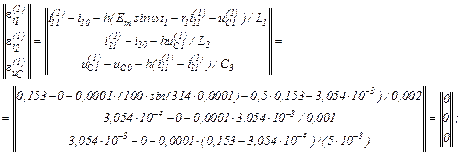
– знаходимо прирости

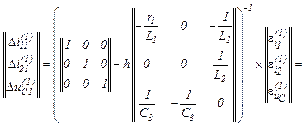
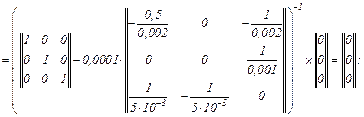
– значення струмів віток та напруги на ємності

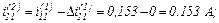
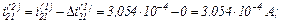
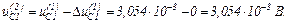
Виконуємо перевірку того, чи досягнута точність, тобто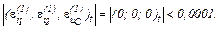

Оскільки точність досягнуто, отримуємо значення струмів віток та напругу
на ємності на першому кроці ітерації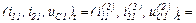

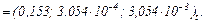
Струм, який протікає через конденсатор

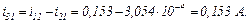
Друга ітерація.

Обчислюємо нульове наближення на підставі явного методу Ейлера

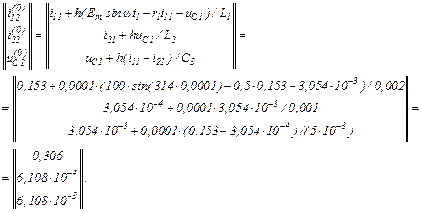
У розгорнутому вигляді система рівнянь має вигляд

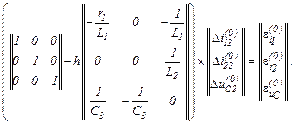
Визначаємо в ітераційному циклі значення струмів віток та напруги на ємності на першому кроці за таким алгоритмом:

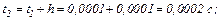
– вектор нев’язок

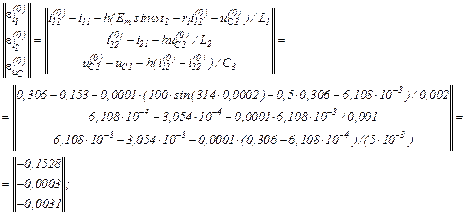
– обчислюємо прирости струмів віток та напруги на ємності

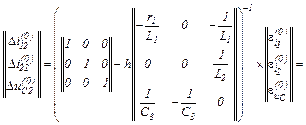
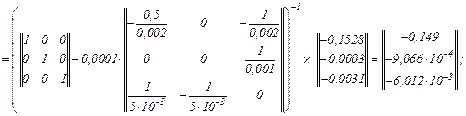
– значення струмів віток та напруги на ємності

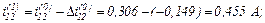
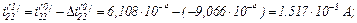
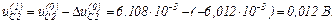
Оскільки 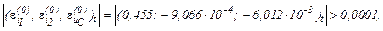про­довжуємо ітераційний процес.

Другий крок в ітераційному циклі:

– обчислюємо вектор нев’язок

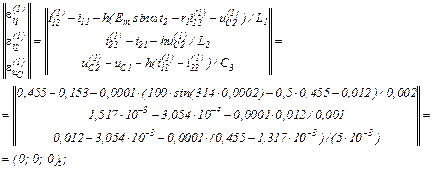
– визначаємо прирости струмів віток та напруги на ємності

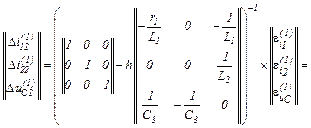
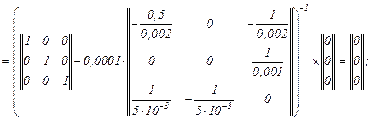
– значення струмів віток та напруги на ємності

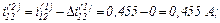
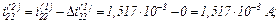
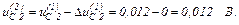
Виконуємо перевірку того, чи досягнута точність, тобто

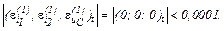
Оскільки точність досягнуто, отримуємо значення струмів віток та напругу на ємності на другому кроці ітерації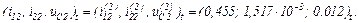

Струм, який протікає через конденсатор

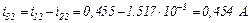
Третя ітерація.

Обчислюємо нульове наближення з використанням явного методу Ейлера

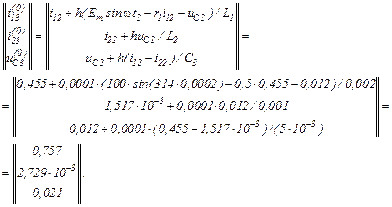
У розгорнутому вигляді система рівнянь має вигляд

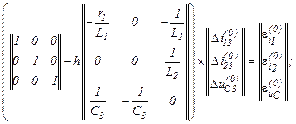
Обчислюємо в ітераційному циклі значення струмів віток та напруги на ємності на першому кроці за таким алгоритмом:

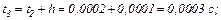
– вектор нев’язок

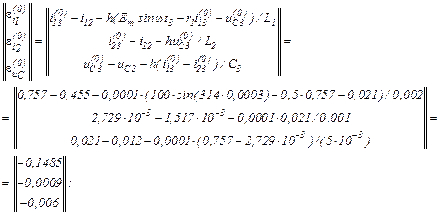
– визначаємо прирости струмів віток та напруги на ємності

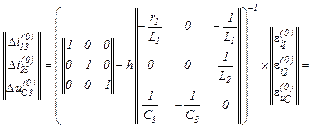
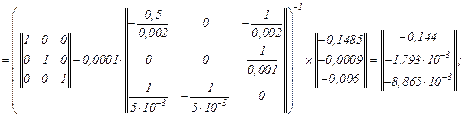
– значення струмів віток та напруги на ємності

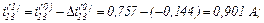
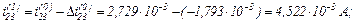
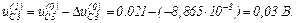
Оскільки 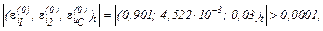продовжу­ємо ітераційний процес.

Другий крок в ітераційному циклі:

– визначаємо вектор нев’язок

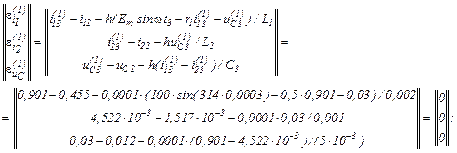
– обчислюємо прирости струмів віток та напруги на ємності

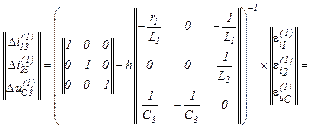
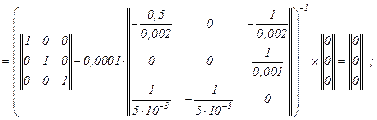
– значення струмів віток та напругу на ємності

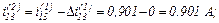
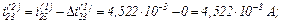
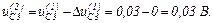
Виконуємо перевірку того, чи досягнута точність, тобто

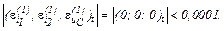
Оскільки точність досягнуто, отримуємо значення струмів віток та напругу на ємності на другому кроці ітерації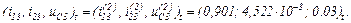

Струм, який протікає через конденсатор

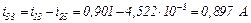
Використовуючи символьну математику MathCad, обчислюємо значення струмів у вітках електричного кола та напругу на ємності, залежності яких показані на рис. 2.12 та рис. 2.13 відповідно.

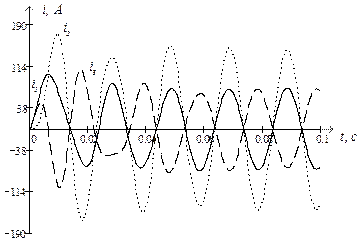
Рис. 2.12. Струми у вітках електричного кола під час вмикання

його на синусоїдну ЕРС

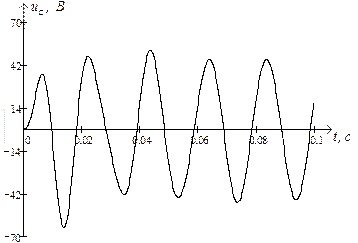
Рис. 2.13. Напруга на ємності ◄

Приклад 7. Метод ФДН.

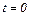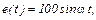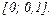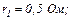
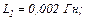
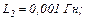
Обчислити неявним методом ФДН другого порядку струми та напругу на ємності в електричному колі (рис. 2.1), яке в момент часу вмикається на ЕРС для інтервалу часу Параметри схеми: 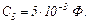До моменту комутації струм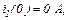 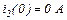та напруга на ємності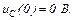

Розв’язання.

Крок інтегрування приймаємо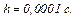

Точність обчислення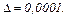

Рівняння, які описують стан електричного кола

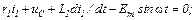
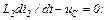
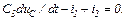
Апроксимуємо в отриманих рівняннях стану похідні за формулою (10.161), в результаті чого одержуємо систему скінченних рівнянь

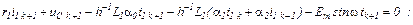
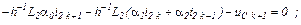
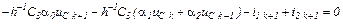
чи в матрично-векторній формі

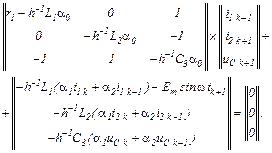
Для постійного кроку 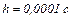на підставі (10.178) записуємо в матрично-векторній формі систему рівнянь

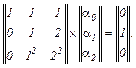
Розв’язавши цю систему рівнянь, отримуємо постійні коефіцієнти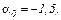

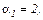
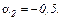
апроксимовану систему рівнянь розв’яжемо на підставі алгоритму Ньютона–Рафсона

Матриця Якобі

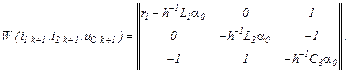
Вектор нев’язок

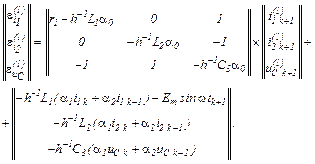
Робоча формула для 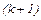-го кроку в 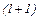-му ітераційному циклі

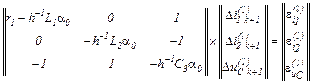
чи в розгорнутому вигляді

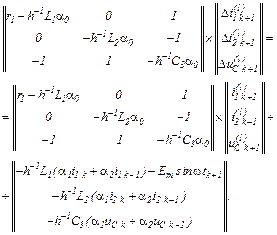
З отриманої системи рівнянь, використовуючи символьну математику MathCad, обчислюємо прирости, тобто

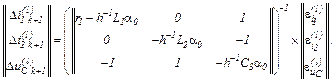
Знаходимо значення координат

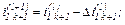
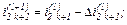
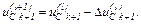
Виконуємо перевірку того, чи досягнута точність на 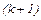-му кроці 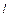ітерації, якщо 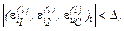тобто менше від заданої точності,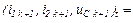 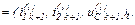В іншому випадку ітераційний процес за вказаним алгоритмом продовжуємо до досягнення заданої точності.

Щоб забезпечити збіжність ітераційного процесу розв’язання апроксимованої сис­теми рівнянь неявним методом ФДН другого порядку з використанням методу Ньютона–Рафсона, нульове наближення виконуємо неявним методом Ейлера першого порядку.

Записуємо вихідну систему рівнянь у нормальній формі Коші

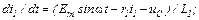
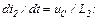
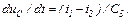
Для отриманої системи рівнянь обчислюємо матрицю Якобі

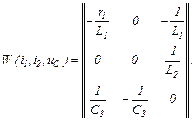
Нульове наближення на кожному ітераційному кроці визначаємо на підставі явної форми Ейлера

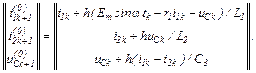
Робоча формула для 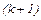-го кроку в 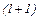-му ітераційному циклі

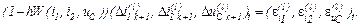
У розгорнутому вигляді

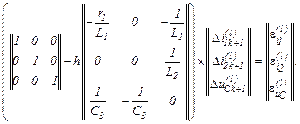
Алгоритм обчислення такий:

– знаходимо вектор нев’язок

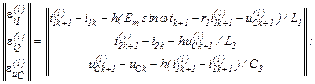
– визначаємо прирости

=

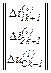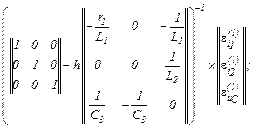
– обчислюємо значення координат

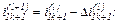
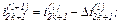
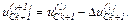
Якщо 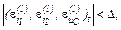тобто менше від заданої точності,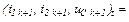 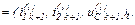В іншому випадку ітераційний процес за вказаним алгоритмом продовжуємо до досягнення заданої точності.

Перша ітерація.

перший крок інтегрування здійснюємо за початковою умовою Коші неявним методом Ейлера.

Обчислюємо нульове наближення для неявного методу Ейлера першого порядку на підставі явного методу Ейлера

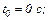
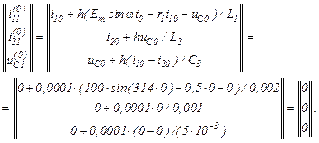
У розгорнутому вигляді система рівнянь має вигляд

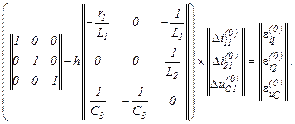
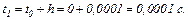
Обчислюємо в ітераційному циклі значення струмів віток та напругу на ємності на першому кроці за таким алгоритмом:

– вектор нев’язок

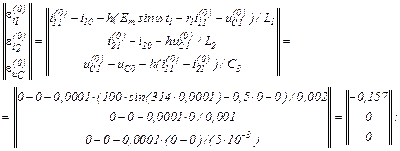
– знаходимо прирости

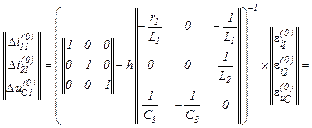
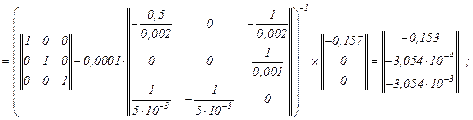
– значення струмів віток та напруги на ємності

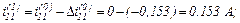
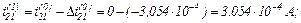
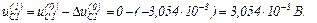
Оскільки 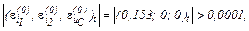продовжуємо ітерацій­ний процес.

Другий крок в ітераційному циклі:

– обчислюємо вектор нев’язок

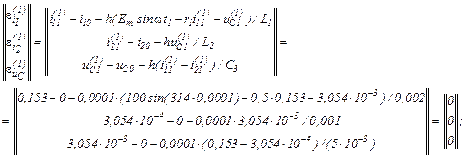
– визначаємо прирости

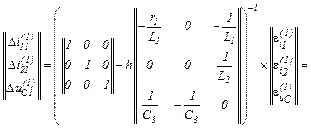
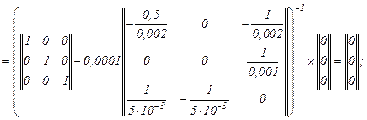
– значення струмів віток та напруги на ємності

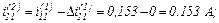
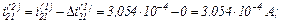
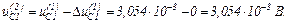
Виконуємо перевірку того, чи досягнута точність, тобто

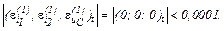
Оскільки точність досягнута, отримуємо значення струмів віток та напругу
на ємності на першому кроці ітерації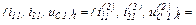

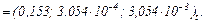
Струм, який протікає через конденсатор

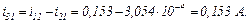
Здійснивши перший крок інтегрування за початковою умовою Коші неявним методом Ейлера, другий крок інтегрування здійснюємо методом ФДН другого порядку за двома попередніми кроками.

Збіжність ітераційного процесу за методом Ньютона–Рафсона забезпечується використанням екстраполяційної формули (10.182) [1, 2] для певного нульового наближення 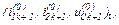яке досить близьке до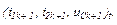

Друга ітерація неявним методом ФДН другого порядку.

Обчислюємо матрицю Якобі для вихідної системи рівнянь

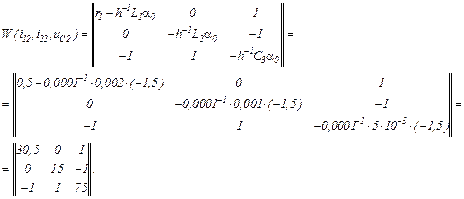
Для постійного кроку 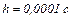на підставі (10.185) записуємо в матрично-векторній формі систему рівнянь, з якої знайдемо коефіцієнти 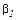та 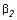для двох попередніх значень координат, тобто

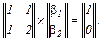
Розв’язавши цю систему рівнянь, отримуємо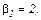

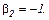
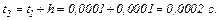
Початкове наближення для ітераційного циклу методу Ньютона–Рафсона

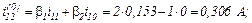
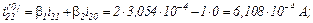
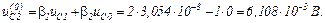
Обчислюємо вектор нев’язок в ітераційному циклі

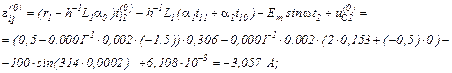
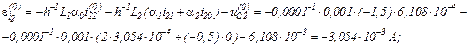
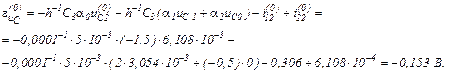
Записуємо в матрично-векторній формі вихідну апроксимовану систему рівнянь

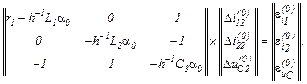
Визначаємо прирости

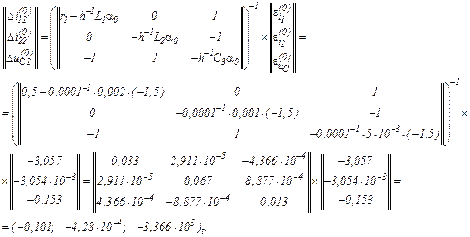
Обчислюємо значення координат

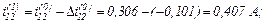
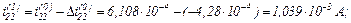
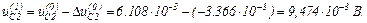
Виконуємо перевірку.

Оскільки 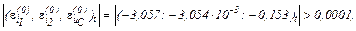про­довжуємо ітераційний цикл.

Другий крок в ітераційному циклі

Визначаємо вектор нев’язок

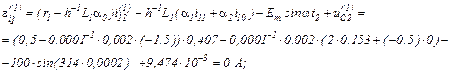
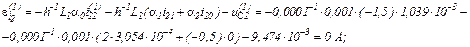
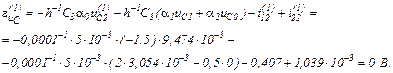
Записуємо в матрично-векторній формі вихідну апроксимовану систему рівнянь

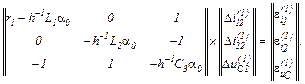
Визначаємо прирости

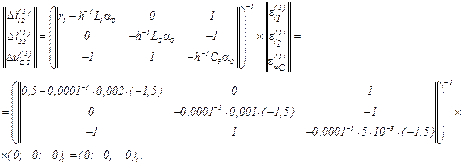
Обчислюємо значення координат

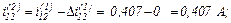
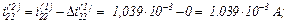
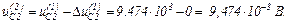
Виконуємо перевірку.

Оскільки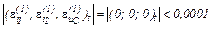

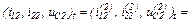
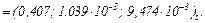
Струм, який протікає через конденсатор

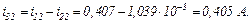
Третя ітерація

Обчислюємо матрицю Якобі для вихідної системи рівнянь

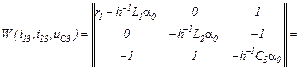
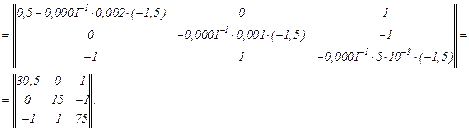
Оскільки обчислено значення координат для трьох попередніх точок, то почат­кове наближення для ітераційного циклу методу Ньютона–Рафсона визначатимемо за трьома попередніми координатами.

на підставі (10.185) записуємо в матрично-векторній формі систему рівнянь, з якої знайдемо коефіцієнти 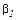та 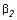для трьох попередніх значень координат, тобто

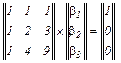
Розв’язавши цю систему рівнянь, отримуємо 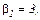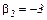та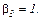

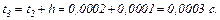
Початкове наближення

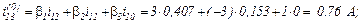
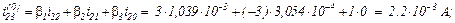
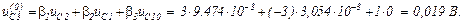
Знайдемо вектор нев’язок

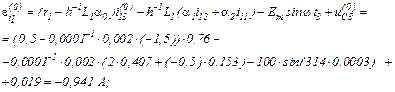
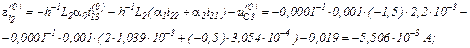
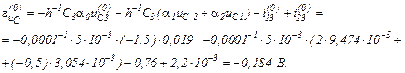
Записуємо в матрично-векторній формі вихідну апроксимовану систему рівнянь

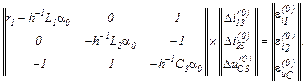
Обчислюємо прирости

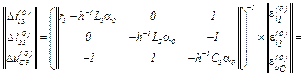
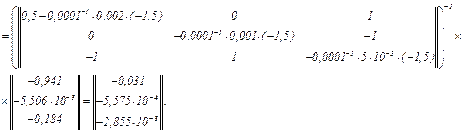
Знаходимо значення координат

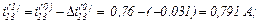
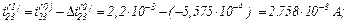
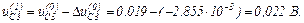
Виконуємо перевірку 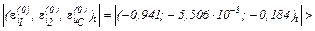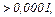продовжуємо ітераційний цикл.

Другий крок в ітераційному циклі

Обчислюємо вектор нев’язок

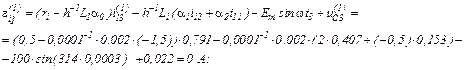
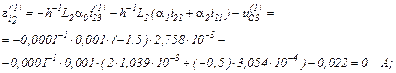
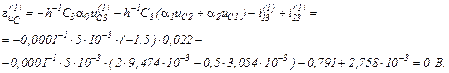
Записуємо в матрично-векторній формі вихідну апроксимовану систему рівнянь

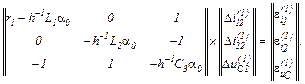
Обчислюємо прирости

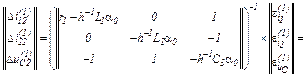
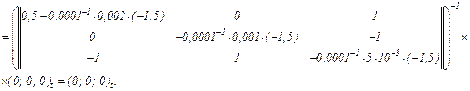
Обчислюємо значення координат

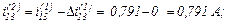
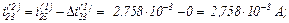
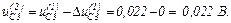
Виконуємо перевірку, оскільки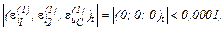

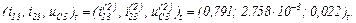
Струм, який протікає через конденсатор

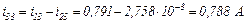
Використовуючи символьну математику MathCad, обчислюємо значення струмів у вітках електричного кола та напругу на ємності, залежності яких показані на рис. 2.14 та рис. 2.15 відповідно.

Рис. 2.14. Струми у вітках електричного кола під час вмикання

його на синусоїдну ЕРС

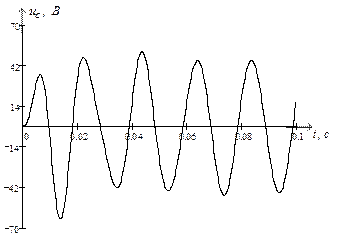
Рис. 2.15. Напруга на ємності ◄

План роботи

1. Ознайомитися з теоретичними відомостями до лабораторної роботи.

2. Сформувати завдання згідно вказаного викладачем варіанту.

3. Сформувати математичну модель.

4. Використовуючи систему символьної математики МаthCad обчислити струми віток електричного кола та напругу на ємності.

5. висновки.

Оформлення звіту

У звіті необхідно навести:

– мету та план роботи;

– короткі теоретичні відомості;

– схему електричного кола;

– математичну модель у методі змінних стану;

– результати розрахунку;

– висновки.

5. Контрольні запитання

1. Якими рівняннями описують перехідні процеси?

2. Запишіть загальну форму системи диференційних рівнянь у неявному вигляді.

3. Як звести систему диференційних рівнянь, записаних у неявному вигляді, до явної форми чи нормальної форми Коші?

4. Як звести систему диференційних рівнянь однієї змінної 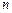-го порядку до нормаль­ної форми Коші?

5. Які додаткові умови необхідно знати під час виділення одного конкретного розв’язку системи диференційних рівнянь?

6. Запишіть алгоритм розв’язання диференційного однорідного рівняння першого порядку зі сталими коефіцієнтами.

7. Запишіть алгоритм розв’язання диференційного однорідного рівняння вищого порядку зі сталими коефіцієнтами.

8. Запишіть алгоритм розв’язання диференційного неоднорідного рівняння першого порядку зі сталими коефіцієнтами.

9. В чому полягає суть методу накладання під час розв’язання диференційних неод­норідних рівнянь?

10. Як принцип накладання використовується для розв’язання лінійних диференцій­них рівнянь зі сталими коефіцієнтами у матрично-векторній формі?

11. Відносно яких змінних складають рівняння, які описують стан електричного кола, і як вони називаються?

12. У чому переваги методу змінних стану під час аналізу стану електричних кіл?

13. Що характеризують змінні стану?

14. Запишіть загальне розв’язання рівнянь змінних стану.

15. У чому полягає суть числових методів розв’язання диференційних рівнянь?

16. Як поділяються числові методи розв’язання диференційних рівнянь?

17. Запишіть загальну формулу дно крокових числових методів розв’язання диферен­ційних рівнянь.

18. Запишіть формулу розв’язання диференційних рівнянь методом Ейлера.

19. Чим визначається ефективність числових методів розв’язання диференційних рівнянь?

20. Запишіть формулу розв’язання диференційних рівнянь методом Ейлера–Коші.

21. Наведіть формулу розв’язання диференційних рівнянь методом Ейлера–Коші з ітераціями.

22. Наведіть робочі формули розв’язання диференційних рівнянь методом Рунге–Кутта.

23. Запишіть робочі формули розв’язання диференційних рівнянь методом Кутта–Мерсона.

24. Як отримують робочі формули розв’язання диференційних рівнянь дно крокових неявних методів?

25. Наведіть робочі формули розв’язання диференційних рівнянь неявним методом Ейлера.

26. Запишіть робочі формули розв’язання диференційних рівнянь неявним методом Ейлера–Коші.

27. Які ітераційні поліноми використовують для виведення робочих формул багато­крокових явних методів?

28. Які методи належать до багатокрокових неявних методів?

29. Запишіть робочі формули розв’язання диференційних рівнянь неявними число­вими методами.

30. Наведіть робочі формули розв’язання диференційних рівнянь методом диферен­ціювання назад.

Список літератури

1. Кириленко О.В., Сегеда М.С., Буткевич О.Ф., Мазур Т.А. Математичне моделювання в електроенергетиці: Підручник / – Львів: Вид-во нац. ун-ту «Львівська політехніка», 2010. – 608 с.

2. Кириленко О.В., Сегеда М.С., Буткевич О.Ф., Мазур Т.А. Математичне моделювання в електроенергетиці: Підручник / 2 – вид. – Львів: Вид-во Львівської політехніки, 2013. – 608 с.

3. Перхач В.С. Математичні задачі електроенергетики – 3-е вид., перероб. і доп. – Львів: Вища шк., 1989. – 464 с.

4. Сегеда М.С. Математичне моделювання в електроенергетиці: Навч. посібник / Мін. освіти і науки України; Національний університет “Львівська політехніка” – Львів: Видавництво Національного університету “Львівська політехніка”, 2002. – 300 с.

5. Чуа Л.О., Пен-Мин Лин. Машинный анализ электрических схем (алгоритмы и вычислительные методы). – М.: "Энергия", 1980. – 640 с.

Завдання

Для заданого електричного кола під час комутації обчислити струми віток електричного кола та напругу на ємності в інтервалі часу 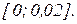Координати та параметри схеми задані в таблиці вихідних даних до завдань: 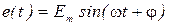. Значення 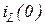та 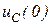до комутації визначається зі схеми.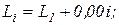

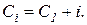
Варіанти схем електричних кіл

Вихідні дані до завдань