Задачи для самостоятельного решения. Докажите формулу:

Задача 1.

Докажите формулу: .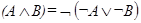

Задача 2.

На вопрос, кто из трёх студентов изучал логику, был известен правильный ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из студентов изучал логику?

Задача 3.

«Вернувшись домой, комиссар Мегрэ позвонил в полицейский отдел на набережную Орфевр.

- Говорит Мегрэ. Есть новости?

- Да, шеф. Поступили сообщения от инспекторов. Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжёт. Жуссье считает, что или Этьен убийца, или Франсуа не был пьян и убийство произошло после полуночи. Инспектор Люка просил передать Вам, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжёт. Затем звонила …

- Всё. Спасибо. Этого достаточно. – Комиссар положил трубку. Он знал, что трезвый Франсуа никогда не лжёт. Теперь он знал всё». Какой вывод сделал Мегрэ?

Указания:

1. Рассмотрите следующие высказывания:

A º {Франсуа был пьян},

B º {Этьен убийца},

C º {Франсуа лжёт},

D º {убийство произошло после полуночи}.

2. Запишите, используя логические операции, высказывания инспекторов Торранса, Жуссье и Люка. Составьте произведение этих трёх высказываний и упростите его.

Задача 4.

Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. На следствии каждый из них сделал два заявления.

Браун: «Я не делал этого. Смит сделал это».

Джонс: «Смит не виновен. Браун сделал это».

Смит: «Я не делал этого. Джонс не делал этого».

Суд установил, что один из них дважды солгал, другой – дважды сказал правду, третий – один раз солгал, один раз сказал правду.

Кто совершил преступление?

Матрицы.

Алгебра матриц

Матрицы, их свойства и действия над матрицами введены в математику для разработки методов решения систем линейных уравнений. В этом разделе Вы научитесь выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы.

Весь материал изложен в доступной форме, приведены соответствующие примеры, так что человек, знакомый с арифметическими действиями для действительных чисел, сможет научиться выполнять действия с матрицами.

Мы минимизировали теоретические выкладки, что-то объясняем «на пальцах» и используем «ненаучные термины». Здесь наша задача – научиться выполнять действия с матрицами. Рассматриваем основы раздела «Алгебра матриц».

Определение: Матрица – это упорядоченная прямоугольная таблица каких-либо элементов, каждый из которых характеризуется двумя натуральными числами: номером строки и столбца, на пересечении которых в матрице он находится.

В качестве элементов матрицыбудем рассматривать числа. Мы рассматриваем числовые матрицы. Элемент – это термин. А элементом «матрицы окон» дома, расположенного напротив Вашего окна, может быть семья, проживающая за данным окном на данном этаже в данном вертикальном ряду.

Обозначения: Матрицы обычно обозначают прописными латинскими буквами, например, как A_{m x n}, справа внизу которых встречаются индексы в виде произведения натуральных чисел (m x n, или m∙n), читается: «m на n». Здесь m – число строк, а n – число столбцов в матрице A. Если m = n, то обозначают A_{n∙ n} = A _n и называют её «квадратная матрица n –го порядка».

Обозначения: Краткая запись выражения «матрица типаA, имеющая m строк и n столбцов, состоящая из таких элементов типа a_ij, что i изменяется от 1 до m, а j изменяется от 1 до n» имеет вид:

A_{m n} = {a_ij | i = 1…m; j = 1…n}.

Здесь, для элементаa_ij,читается: «а и жи», но не «а и на жи»!

Пример:

Рассмотрим матрицу «два на три»:

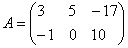
Данная матрица состоит из шести элементов:

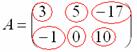
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:

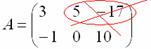
Это просто таблица (набор) чисел!

Также договоримся не переставлять числа, если иного не сказано в объяснениях.

У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки:

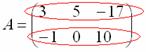
и три столбца:

СТАНДАРТ:когда говорят о размерах матрицы, то сначалауказывают количество строк, а только потом – количество столбцов.

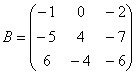Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например:

– это матрица «три на три».

Если в матрице один столбец

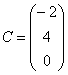или одна строка 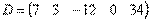, то такие матрицы также называют векторами.

Теперь переходим непосредственно к изучению действий с матрицами: