Тема 1. Основные задачи математической физики

Министерство образования и науки Республики Казахстан

Павлодарский государственный университет им. С. Торайгырова

Кафедра информатики и информационных систем

Опорный конспект лекции

дисциплины «Численные методы решения задач математической физики»

для специальности 050601 Математика

Павлодар

Форма Ф СО ПГУ 7.18.1/07

УТВЕРЖДАЮ

Проректор по УР

_________ Н.Э. Пфейфер

"___" __________200__г.

Составители: доцент Даутова А.З.,

Преподаватель Оспанова Г.А.

Кафедра «Информатика и информационные системы»

Опорный конспект лекции

по дисциплине «Численные методы решения задач математической физики»

для студентов специальностей 050601 Математика

Рекомендована на заседании кафедры от “____”___200___г.

Протокол № ___

Заведующая кафедрой ___________ Ж.К.Нурбекова

Одобрена методическим советом факультета Физики, математики и информационных технологий “___”______200_г. Протокол №___

Председатель МС__________________________ А.З. Даутова

Тема 1. Основные задачи математической физики.

Разностные уравнения. Пространство сеточных функций. Разностные операторы. Разностная аппроксимация оператора Лапласа. Задачи на собственные значения для разностного оператора Лапласа. Разностные формулы Грина. Свойства разностных операторов. Априорные оценки. Аппроксимация дифференциальной начально-краевой задачи разностной схемой. Шаблон. Порядок аппроксимации. Определение устойчивости. Аппроксимация нормированного пространства. Внутренние и внешние аппроксимации. Невязка. Ошибка аппроксимации. Устойчивость. Сходимость.

Решение обыкновенных дифференциальных уравнений зависит лишь от одной переменной 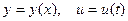и так далее. Во многих практических задачах решения - искомые функции зависят от нескольких переменных и уравнения, описывающие данные задачи могут содержать частные производные искомых функции. Они называются уравнениями с частными производными.

Математическая постановка задачи вместе с дифференциальными уравнениями содержит и некоторые дополнительные условия. Если решение ищется в ограниченной области, то задаются условия на ее границе, называемые граничными (краевыми) условиями. Такие задачи носят названия краевых задач для уравнений с частными производными.

Задача, которая состоит в решении уравнений при заданных начальных условиях, называется задачей Коши (ЗК) для уравнений с частными производными. При этом задача решается в неограниченном пространстве, и граничные условия не задаются. Задача, у которой ставится, и начальные и граничные условия называются нестационарными (смешанными) краевыми задачами. Получающиеся при этом решения меняются с течением времени.

Задачи, решение которых существует и единственно в некотором классе начальных и граничных условий и непрерывно зависит как от этих условий, так и от коэффициентов этих уравнений, называются корректно поставленными.

Среди численных методов рассмотрим разностные методы, которые основаны на введение некоторой разностной сетки в рассматриваемой области. Все значения производных, начальные и граничные условия выражаются через значения функции в узлах сетки, в результате чего получается система линейных уравнений, называемая разностной схемой. Построение разностных схем решения уравнений с частными производными основано на введение сетки в рассматриваемой области. Узлы сетки являются расчетными точками.

a£x£b x_i=a+ih₁ (I=0,1,…,I)

c£y£d y_j=c+jh₂ (j=0,1,…,J)

Для построения разностной схемы, частные производные в уравнений заменяются, конечно- разностными соотношениями по некоторому шаблону. При этом точные значения искомой функции U заменяются значениями сеточной функции u в узлах разностной сетки.

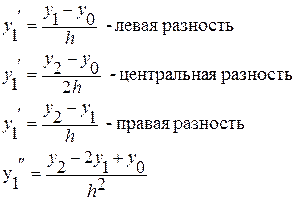
Разностная схема для решения уравнения теплопроводности при заданных начальных и граничных условий имеет следующий вид:

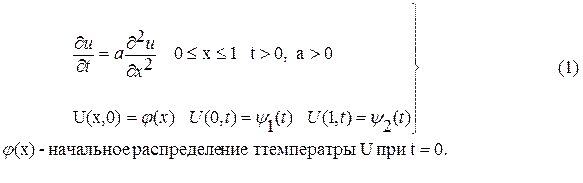
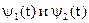- распределение температуры на концах рассматриваемого отрезка [0,1] в любой момент, начальные и граничные условия должны быть согласованы, то есть 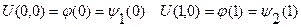. Вводим прямоугольную сетку:

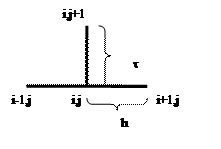
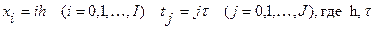- шаги. 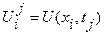- значение функции в узлах сетки. Таким образом,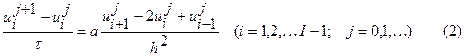

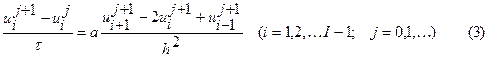
Получаем систему алгебраических уравнений для определения значений сеточных функции во внутренних узлах. Из граничного условия

(4)

При 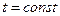совокупность узлов называется слоем. Из (2) находим последовательно значения 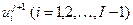на 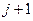слое через соответствующие значения 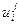на 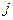- том слое. Такие схемы называются явными. Для начала счета при 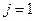необходимо решение на начальном слое, которое определяется начальным условием, имеющим следующий вид:

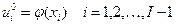(5)

В отличие от явной схемы каждое разностное уравнение (3) содержит на каждом новом слое значения неизвестных в трех точках, поэтому нельзя сразу определить эти значения через известное решение на предыдущем слое. Они носят названия неявных схем. При этом разностная схема (3) состоит из линейных трехточечных уравнений, то есть каждое уравнение содержит неизвестную функцию в трех точках данного слоя. Решаются методом прогонки.

В данном примере рассматривали двухслойную схему, т.е. в каждое разностное уравнение входят значения функции их двух слоев – нижнего, на котором решение уже найдено, и верхнего, в узлах которого решение ищется.

Сходимость. Аппроксимация. Устойчивость.

Дифференциальная задача состоит в решение уравнения с частными производными при заданных начальных и граничных условии записывается в операторном виде:

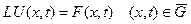(6)

Операторное уравнение включает исходное уравнение с частными производными, и дополненное, включающее начальные и граничные условия. 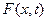описывает правые части уравнения, начальные и граничные условия, 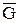включает и расчетную область, и границу. Дифференциальную задачу (6) заменяем разностной задачей, где 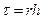, где .

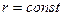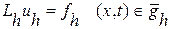(7)

Значение сеточной функции 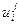в узлах сетки 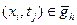приближенно заменяют значения искомой функции 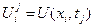в тех же узлах с погрешностями

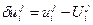. (8)

Вводим .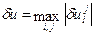

Разностная схема (7) называется сходящейся, если при сгущении узлов сетки, это значение погрешности стремится к нулю, т.е. если 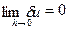(9).

Если 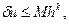где 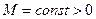, то разностная схема имеет k-ый порядок точности или говорят, что она сходится со скоростью .

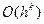Запишем уравнение (7) для погрешности решения на сетке 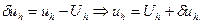. Подставляя в (7), имеем 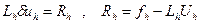(10)

Величина 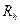называется невязкой ( погрешностью аппроксимации) разностной схемы. Вводим характеристическую величину

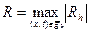(11)

при 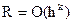аппроксимация имеет k- ый порядок относительно h. Разностная схема (7) аппроксимирует исходную дифференциальную задачу (6), если при измельчении сетки невязка стремится к нулю, т.е. если

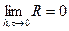(12)

Абсолютной (безусловной) аппроксимацией называется аппроксимация такого типа, когда невязка стремится к нулю при 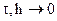по любому закону без каких- либо условий. При условной аппроксимации налагаются некоторые условия на размеры шагов по пространству и времени. Разностная схема (7) называется устойчивой, если ее решение непрерывно зависит от входных данных, т.е. малому изменению входных данных соответствует малое изменение решения. Устойчивость характеризует чувствительность разностной схемы к различного рода погрешностям.

Теорема: Если решение исходной дифференциональной задачи (6) существует, а разностная схема (7) устойчива и аппроксимирует (6) на данном решение, то разностное решение сходится к точному.

[1] - [5], введение, глава 5