Заочной (обычной) формы обучения ФЭФ

Задания к зачету по дисциплине «Высшая математика»

Для студентов II курса осеннего семестра

заочной (обычной) формы обучения ФЭФ

Раздел 1. «Элементы теории вероятностей»

Тема. «Классическое определение вероятности»

1. Из букв разрезной азбуки составлено слово «воздух». Карточки с отдельными буквами тщательно перемешивают, затем наугад извлекают и раскладывают их в порядке извлечения. Какова вероятность того, что:

а) получится слово «воздух»;

б) из трех извлеченных карточек получится слово «ухо».

Ответ: а) 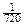; б) .

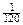2. Из букв разрезной азбуки составлено слово «симметрия». Карточки с отдельными буквами тщательно перемешивают, затем наугад извлекают и раскладывают их в порядке извлечения. Какова вероятность того, что:

а) получится слово «симметрия»;

б) из четырех извлеченных карточек получится слово «метр».

Ответ: а) 0,000011; б) 0,000661.

3. Из букв разрезной азбуки составлено слово «кокос». Карточки с отдельными буквами тщательно перемешивают, затем наугад извлекают и раскладывают их в порядке извлечения. Какова вероятность того, что:

а) получится слово «кокос»;

б) из трех извлеченных карточек получится слово «сок».

Ответ: а) 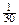; б) .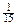

4. Из 20 сбербанков 10 расположены за чертой города. Для аудиторской проверки случайно выбраны 5 сбербанков. Какова вероятность того, что только 2 из них окажутся в черте города.

Ответ: 0,3483.

5. В урне 8 белых и 7 черных шаров. Какова вероятность того, что среди извлеченных наугад семи шаров окажутся 4 черных?

Ответ: 0,3046.

6. В партии, состоящей из 25 холодильников, 5 имеют скрытые дефекты. Наугад отбирают 4 холодильника. Какова вероятность того, что один из них имеет скрытый дефект?

Ответ: 0,45059.

Тема. «Теоремы сложения и умножения вероятностей»

7. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,78, а для второго – 0,82. Найти вероятность того, что при одном залпе в мишень попадает:

а) только один из стрелков;

б) хотя бы один из стрелков.

Ответ: а) 0,3208; б) 0,9604.

8. В одном из офисов фирмы имеется 3 телефона. Вероятность занятости каждого из них равны соответственно 0,2; 0,1; 0,15. Найти вероятности того, что:

а) только один из телефонов занят;

б) хотя бы один из телефонов занят.

Ответ: а) 0,329; б) 0,388.

9. В телестудии три телевизионные камеры. Вероятности того, что в данный момент камера включена, равны соответственно 0,9; 0,8 и 0,95. Найти вероятность того, что в данный момент включены:

а) только две камеры;

б) хотя бы одна камера.

Ответ: а) 0,283; б) 0,999.

10. Имеются две урны с шарами трех цветов. В первой находится 2 синих, 3 красных, 5 зеленых, а во второй находятся 4 синих, 2 красных, 4 зеленых. Из каждой урны извлекают по одному шару и сравнивают их цвета. Найти вероятность того, что цвета извлеченных шаров одинаковы.

Ответ: 0,34.

Тема. «Формула полной вероятности. Формула Байеса»

11. Комплектовщик получает для сборки 32% деталей с завода № 1, остальные – с завода № 2. Вероятность того, что деталь с завода № 1 – бракованная равна 0,02, для детали с завода № 2 – 0,03. Найти вероятность того, что:

а) случайно взятая деталь – бракованная;

б) наугад взятая деталь оказалась бракованной. Какова вероятность того, что она изготовлена на заводе № 1.

Ответ: а) 0,0268; б) 0,23881.

12. Заготовка может поступить для обработки на один из трех станков с вероятностями 0,4; 0,25 и 0,35 соответственно. При обработке на первом станке вероятность брака составляет 1,2%, на втором – 2%, на третьем – 1,8%. Найти вероятность того, что:

а) наугад взятое после обработки изделие − стандартное;

б) наугад взятая изделие после обработки оказалась стандартным. Какова вероятность того, что оно обработано на третьем станке.

Ответ: а) 0,9839; б) 0,34932.

13. В данном районе изделия поставляются двумя фирмами в соотношении 5:8. Среди продукции первой фирмы стандартное изделие составляет 90%, второй – 85%. Найти вероятность того, что:

а) наугад взятое изделие − стандартное;

б) наугад взятая изделие оказалась стандартным. Какова вероятность того, что оно изготовлено второй фирмой.

Ответ: а) 0,86925; б) 0,60176.

14. В ремесленном цехе трудится 3 мастера и 6 их учеников. Мастер допускает брак при изготовлении изделия с вероятностью 0,05; ученик – с вероятностью 0,15. Найти вероятность того, что:

а) поступившее из цеха изделие − бракованное;

б) поступившее изделие оказалась бракованным. Какова вероятность того, что оно изготовлено мастером.

Ответ: а) 0,11667; б) 0,14285.

Тема. «Формула Бернулли»

15. Всхожесть семян некоторого растения составляет 80 %. Найти вероятность того, что из семи посеянных семян взойдут только три.

Ответ: .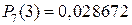

16. Вероятность успешной сдачи студентом каждого из пяти экзаменов равна 0,7. Найти вероятность того, что студент успешно сдаст только три экзамена.

Ответ: .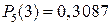

17. Среди изделий, подвергшихся термической обработке, в среднем 92 % высшего сорта. Найти вероятность того, что среди шести изделий только четыре высшего сорта.

Ответ: .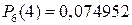

18. Оптовая база обслуживает 6 магазинов. Вероятность получения заявки базой на данный день для каждого из магазинов равна 0,65. Найти вероятность того, что в этот день будет только пять заявок.

Ответ: .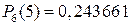

Тема. «Дискретные случайные величины»

19. Пуст СВ X задана законом распределения

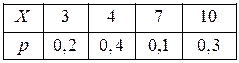
Найти функцию распределения F(X) и построить ее график. Вычислить , .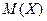

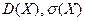Ответ: M(X)=5,9; D(X)=8,29; s(X)=2,879.

20. Дан ряд распределения ДСВ :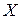

X	-3	−1,5	0,5
p	0,15	0,2	0,55	0,1

Найти:

1) функцию распределения СВ X и построить ее график;

2) математическое ожидание, дисперсию, среднее квадратическое отклонение;

21. Дан ряд распределения ДСВ :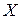

X	-1		2,5	3,5
p	0,1	0,3		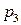0,25

Найти:

1) ;

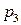2) функцию распределения СВ X и построить ее график;

3) математическое ожидание, дисперсию, среднее квадратическое отклонение;