Выбор прогнозируемых характеристик кусковатости
Практически каждое крупное исследование, ставившее своей целью изучение действия взрыва в горных породах, в той или иной степени затрагивало проблему прогнозирования результатов разрушения.
В работах о статистике образования кусков указывается, что в самых простых моделях распределения размеров кусков имеется по крайней мере, два независимых параметра, изменение каждого из которых может существенно менять остальные характеристики кусковатости. Между тем в работах о прогнозировании кусковатости при взрывном разрушении рассматривается большей частью только одна характеристика кусковатости. Причем экспериментальные исследования подтверждают выведенные таким образом зависимости в широком диапазоне изменения параметров взрыва и характеристик гранулометрического состава горной массы.
В качестве характеристик гранулометрического состава обычно выбирали чисто технологические характеристики: выход негабарита, выход кондиционной фракции (-400, -500, -800 мм и т.п.). В последнее время принято прогнозировать статистически значимую характеристику - средний арифметический размер куска (математическое ожидание размеров кусков горной массы).
Наиболее общие предположения о характере последовательного дробления определяют в качестве предельных следующие законы распределения размеров, поверхностей или объемов кусков:
1) логарифмически-нормальный в том случае, когда вероятность дробления каждого отдельного куска не зависит от его размеров (схема Колмогорова);
2) гамма-распределение и его разновидности в том случае, когда вероятность дробления увеличивается пропорционально какой-либо положительной степени размера куска (схема Колмогорова - Филиппова).
Вся совокупность кусков, включающая несколько порядков размеров, образована в результате сложных процессов и может быть аппроксимирована в какой-либо части одной из этих моделей.
Методика определения кусковатости взорванной горной мас-
сы анализирует лишь крупную часть ее в пределах одного порядка
размеров. Соотношение размеров кусков этой части в наибольшей
степени влияет на производительность машин погрузочно-транс-
портного комплекса. В пределах этого диапазона размеров можно
считать удовлетворительной логарифмически-нормальную аппрок-
симацию, тем более, что опыт показывает хорошее соответствие
гистограмм распределения размеров редко полному, чаще усечен-
ному логарифмически-нормальному закону в широком диапазоне из-
менения параметров отбойки. При этом аналогичные по физико-ме-
ханическим свойствам горные породы при различных параметрах
разрушения дают подобные законы распределения, у которых ме-
няется лишь математическое ожидание размеров и сохраняется
постоянная логарифмическая дисперсия.
Этот экспериментальный факт дает возможность анализировать изменение кусковатости по одному из двух независимых параметров закона распределения.
Условие свободной вариации параметров закона распределения предполагает наличие двух экстремальных случаев: один (с нулевой логарифмической дисперсией) характеризует гранулометрический состав, включающий куски одного размера, другой (с бесконечно большой дисперсией) - горную массу с частицами любых размеров и бесконечно малым содержанием каждой фракции в совокупности.
Между этими двумя крайними случаями, которые никогда не встречаются в реальных условиях, располагается достаточно большое число наборов кусков, имеющих одинаковое математическое ожидание размеров и существенно разное их распределение. Следовательно, характеризовать гранулометрический состав горной массы одним параметром: негабаритом, выходом кондиционных кусков, средним размером и т.п. - неправомерно. Ведь при абсолютно одинаковых показателях такого рода другие характеристики гранулометрического состава при свободной вариации второго показателя закона распределения, отвечающего за разброс размеров кусков, могут быть существенно разными. Необходимо проанализировать материал технологического опробования горной массы с тем, чтобы оценить возможную вариацию логарифмической дисперсии при логарифмически-нормальной аппроксимации данных.
Накопленные данные гранулометрического анализа пород различной трещиноватости на ряде предприятий дали возможность ответить на этот вопрос.
Многолетние исследования гранулометрического состава горной массы, проведенные на комбинате «Апатит» (скважинная, шпуровая и минная отбойка), на Ждановском карьере комбината «Печенганикель», на Оленегорском карьере, карьере «Медвежий Ручей» НГМК, карьерах ЮГОК и НКГОК Криворожского бассейна, джезказганском карьере (при различных параметрах буровзрывных работ), исследования кусковатости и трещиноватости пород Тургоякского месторождения и рудника «Каратау», а также кусковатости в зоне ядерных подземных взрывов (данные ученых США) показали, что при среднем размере куска, меняющемся в 8 раз (от 60 до 450 мм) средняя логарифмическая дисперсия мало отличается от единицы.
Сводные данные этих исследований, приведенные к среднему размеру около 100 мм с 10-процентным доверительным интервалом, наглядно представляют вариации логарифмической дисперсии этих распределений (рис. 11) при Квар = 15 %. Доверительный интервал этой характеристики по выборке из 41взрыва объемом 500 тыс.м3 каждый укладывается в 4%.
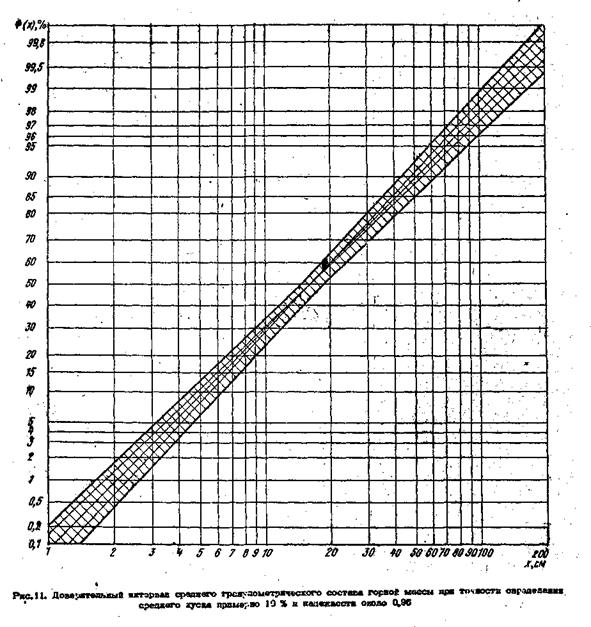 |
Малая вариация показателя разброса размеров кусков горной массы свидетельствует о том, что при разрушении разнородных массивов пород различными способами, включая и естественное разрушение (данные по трещиноватости), реализуется лишь малая часть возможных статистических моделей. Можно сказать, что практически результата разрушения, оцениваемые логарифмически-нормальным законом распределения, в исследованном диапазоне изменения среднего размера куска - подобны.
Полезно отметить то важное обстоятельство, что образова-
ние схемы блоков в результате многовекового нагружения масси-
ва и образование системы кусков при кратковременном взрывном
нагружении обуславливаются одинаковыми статистическими причи-
нами, физическая природа которых не ясна. Однако нельзя ска-
зать, что взрыв копирует разрушение системы блоков, поскольку
разрушение затрагивает нетронутые части массива, образуя при
этом подобные формы кусков с малоотличающейся дисперсией рас-
пределения кусков.
Отмеченную особенность процесса разрушения горных пород необходимо учитывать при решении чисто технологических задач горного производства и, в частности, задачи равномерного дробления массива.
Итак, задача получения регулярного или более равномерного дробления путем изменения параметров буровзрывных работ (БВР) неправильна в постановке. Материалы производственных исследований свидетельствуют, что любые возможные изменения параметров БВР не могут целенаправленно воздействовать на показатель разброса распределения размеров. Предлагаемые расчетные методы получения равномерного дробления предусматривают регулирование этого показателя за счет изменения формы импульса, передаваемого от заряда к породе. Технологически это выражается в изменении удельного расхода ВВ по длине заряда или на различных участках взрываемого массива.
Экспериментальный материал по регулированию дробления отсутствует, а те данные, которые прослеживают изменение характеристик кусковатости при вариации удельного расхода, не дают основания надеяться на успешную реализацию такого способа обеспечения равномерности дробления.
Широкая вариация уровня удельного расхода ВВ не сказывается на показателе равномерности дробления (логарифмической дисперсии).
Узкий диапазон и случайный характер изменения логарифмической дисперсии распределения размеров кусков взорванной горной массы позволяет регулировать степень дробления только за счет увеличения или уменьшения крупности среднего размера куска. При этом повышение равномерности дробления означает на самом деле уменьшение содержания крупных фракций за счет увеличения количества мелочи, т.е. той доли совокупности кусков, которая не влияет существенно на работу погрузочно-транспортного комплекса карьеров.
Таким образом, отмеченная особенность формирования совокупности кусков горной массы при взрыве позволяет рассматривать при сравнении различных наборов кусков в качестве основной и единственной характеристики лишь один параметр закона распределения - средний размер куска или математическое ожидание размеров.
Косвенным доводом в пользу этого положения служит тот факт, что существует целый класс эмпирических зависимостей, связывающих параметры буровзрывных работ и производительность добычных и транспортных машин со средним размером куска горной массы. Причем каждая из этих зависимостей подтверждается значительным объемом производственных наблюдений в широком диапазоне изменений параметров.
При изучении методов прогнозирования гранулометрического состава горной массы это положение использовалось неоднократно, хотя его физическая природа не исследовалась.
Эксперименты показали, что той же особенностью обладают распределения буровой мелочи, аппроксимируемые гамма-распределением (законом Розина - Рамилера).
Можно предположить, что и в случае многомодальных распределений будет сохраняться постоянным показатель разброса по отношению к каждой моде. Особенности фотопланиметрического анализа позволяют выделить во взорванной горной массе лишь одну моду, соответствующую наиболее крупным элементам совокупности, для которой и найдено значение логарифмической дисперсии, равное единице. Моды более мелких элементов распределения имеют большее значение логарифмической дисперсии.
