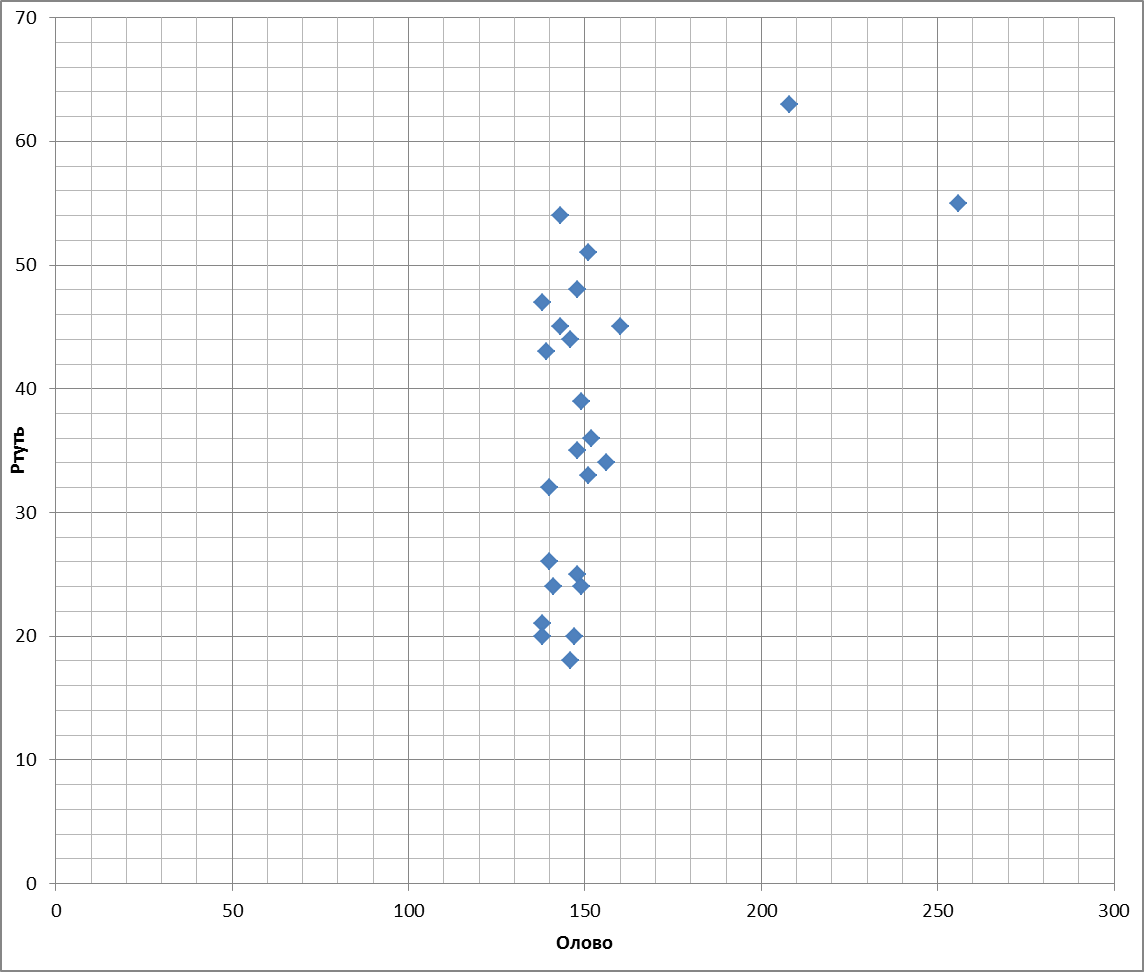
Этап 6. Построение корреляционного поля и вычисление момента корреляции

Этап 1. Выделение геолого-геохимических блоков

1 участок

Профиль	Пикет	Ртуть	Олово

2 участок

Профиль	Пикет	Ртуть	Олово

Этап 2. Изучение распределений и связи химических элементов.

Ртуть (Hg)

1) Находим минимум и максимум среди значений содержания

ртути, попавших в первый участок:

Min = 18 max = 63

2) Затем при помощи шага разбиваем на шесть интервалов, шаг вычисляется по формуле:

∆ = (max-min)/6 = (63-18)/6 = 7,5

3) Далее вычисляем частоту (n(i)), частость (p(i)) и накопленную частость (h(i)).

Частота – это количество значений, попавших в каждый интервал. Частота вычисляется по формуле:

P(i) = 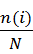* 100%

Где N (сумма всех значений) = 24

4) Накопленная частость вычисляется по формуле:

h(1) = p(1); h(2) = p(1) + p2; h(3) = h(2) + p(3) и т.д.

Сумма всех шести h(i) должна быть равна 100

Таблица 1

Граница интервалов X(i)	Частота n(i)	Частость p(i) * 100%	Накопленная частота h(i)
от	до
	25,5		29,2	29,2
25,5			8,3	37,5
	40,5		20,8	58,3
40,5			20,8	79,1
	55,5		16,7	95,8
55,5			4,2

Олово(Sn)

1) Находим минимум и максимум среди значений содержания олова, попавших в первый участок:

Min = 138 max = 256

2) Затем при помощи шага разбиваем на шесть интервалов, шаг вычисляется по формуле:

∆ = (max-min)/6 = (256-138)/6 = 19,7

3) Далее вычисляем частоту (n(i)), частость (p(i)) и накопленную частость (h(i)).

Частота – это количество значений, попавших в каждый интервал. Частота вычисляется по формуле:

P(i) = 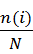* 100%

Где N (сумма всех значений) = 24

4) Накопленная частость вычисляется по формуле:

h(1) = p(1); h(2) = p(1) + p2; h(3) = h(2) + p(3) и т.д.

Сумма всех шести h(i) должна быть равна 100

Таблица 2

Граница интервалов X(i)	Частота n(i)	Частость p(i) * 100%	Накопленная частота h(i)
от	до
	157,7		87,5	87,5
157,7	177,4		4,2	91,7
177,4	197,1			91,7
197,1	216,8		4,1	95,8
216,8	236,5			95,8
236,5	256,2		4,2

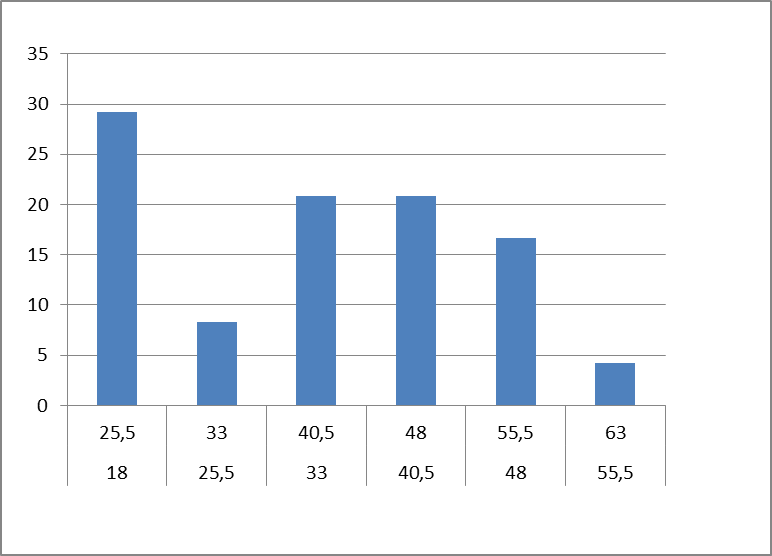
Этап 3. Построение гистограмм

Используя значения частостей и границы интервалов, строим гистограмму

Ртуть (Hg)

Олово (Sn)

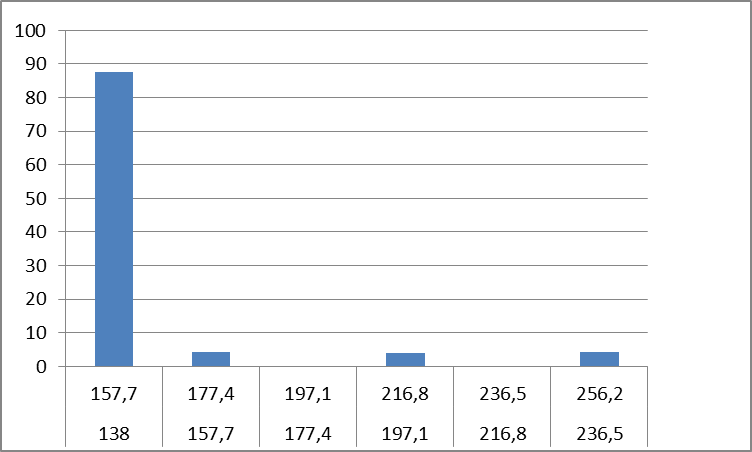
Этап 4. Построение накопленных частостей

Используя значения накопленных частостей и границ интервалов, строим линии накопленных частостей.

Ртуть (Hg)

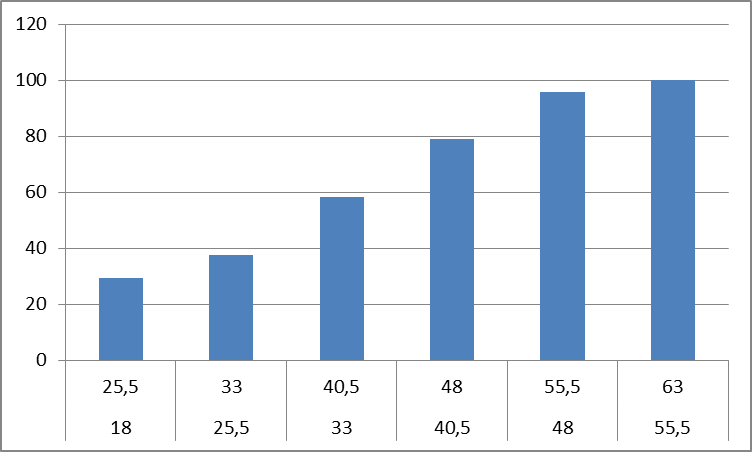
Олово (Sn)

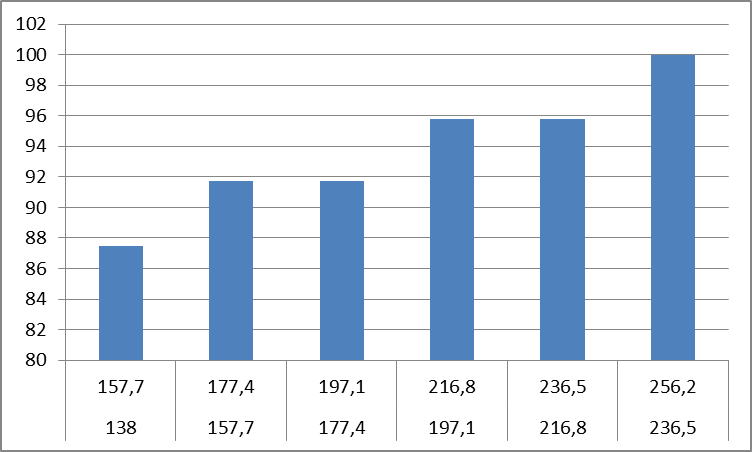
Этап 5. Расчёт параметров распределения для Hg и Sn

Ртуть (Hg)

Исходные значения:

Хср = 36.75

М2 = 157.27

М3 = 389.97

M4 = 49364.81

Логарифмические значения:

Хср = 1,54

М2 = 0.0245

М3 = -0.0009

М4 = 0.001

Используя значения оценок центральных моментов, вычисляем оценки дисперсии, стандартного отклонения, коэффициентов вариации, ассиметрии и экцесса, как для исходных значений, так и для логарифмов, по следующим формулам:

S2 = N * M2/N - 1

S = √S2

V = S/Xср * 100%

A = M3/S3

E = (M4/S4) -3

Для исходных значений

S2 = N * M2/N - 1 = 24 * 157,27/23 = 164,11

S = √S2 = 12,81

V = S/Xср * 100% = 12,81/36,75* 100%=34,86

A = M3/S³ = 389,97/(12,81)³=0,19

E = (M4/S⁴) -3 = (49364,81/(12,81)⁴) – 3 = -1,17

Затем сравниваем отношения, где е и а находятся по формулам:

а = √(6/24) = 0,5

е = √(24/24) = 1

Если значения отношений <3 каждое, то гипотеза о соответствии выборочного распределения теоретически (нормальному или логарифмическому) принимается.

А/ а =0,38< 3

Е/ е = -1,17< 3

Закон распределения соответствует нормальному.

Для логарифмов

S2 = N * M2/N - 1 = 24 * 0,025/23 = 0,026

S = √S2 = 0,16

V = S/Xср * 100% = 0,16/1,54* 100% = 10,4%

A = M3/S³ = -0,0009/(0,16)³= -0,22

E = (M4/S⁴) -3 = 0,001/(0,16)⁴ – 3 = -1,47

Затем сравниваем отношения, где е и а находятся по формулам:

а = √(6/24) = 0,5

е = √(24/24) = 1

Если значения отношений <3 каждое, то гипотеза о соответствии выборочного распределения теоретически (нормальному или логарифмическому) принимается.

А/ а = -0,44 < 3

Е/ е = -1,47 < 3

Закон распределения соответствует нормальному логарифмическому.

Олово (Sn)

Исходное значение:

Хср = 153,13

М2 = 645,61

М3 = 51302,01

М4 = 5057650

Логарифмическое значение:

Хср = 2,18

М2 = 0,005

М3 = 0,0006

М4 = 0,0001

Для исходных значений:

S2 = N * M2/N - 1 = 24 * 645,61/23 = 673,68

S = √S2 = 26

V = S/Xср * 100% = 26/153,13* 100% = 17%

A = M3/S3 = 51302,01/(26)³= 2,92

E = (M4/S4) -3 = (5057650/(26)⁴) – 3 = 8,1

Затем сравниваем отношения, где е и а находятся по формулам:

а = √(6/24) = 0,5

е = √(24/24) = 1

Если значения отношений <3 каждое, то гипотеза о соответствии выборочного распределения теоретически (нормальному или логарифмическому) принимается.

А/ а = 5,84 > 3

Е/ е = 8,1 >3

Закон распределения не соответствует нормальному.

Для логарифмов

S2 = N * M2/N - 1 = 24 * 0,005/23 = 0,005

S = √S2 = 0,07

V = S/Xср * 100% = 0,07/2,18 * 100% = 3,2%

A = M3/S3 = 0,0006/(0,07)³ = 1,75

E = (M4/S4) -3 = (0,0001/(0,07)⁴) – 3 = 1,16

Затем сравниваем отношения, где е и а находятся по формулам:

а = √(6/24) = 0,5

е = √(24/24) = 1

Если значения отношений <3 каждое, то гипотеза о соответствии выборочного распределения теоретически (нормальному или логарифмическому) принимается.

А/ а = 3,5 > 3

Е/ е = 1,16 < 3

Закон распределения не соответствует нормальному.

Этап 6. Построение корреляционного поля и вычисление момента корреляции.

Строим корреляционное поле для основного и попутного компонентов. По оси абсцисс откладываем содержание основного компонента, в данном случае Hg, а по оси ординат – содержание попутного, т.е. Sn.

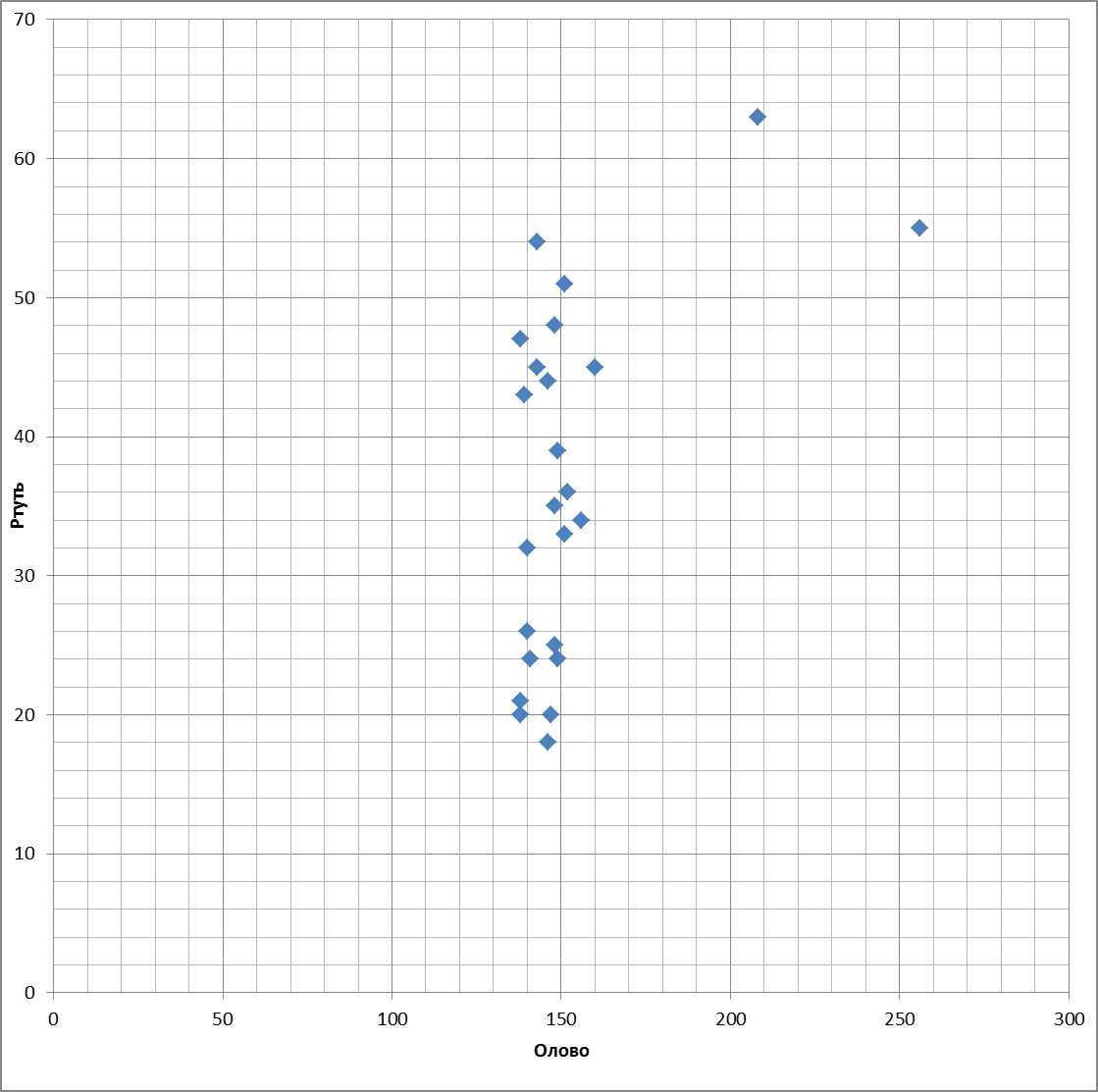
Для предварительной оценки силы связи на корреляционном поле необходимо провести линии, соответствующие медианам значений основного и попутного компонентов, разделив ими поле на четыре квадрата.

Количественной мерой силы связи является коэффициент корреляции. Его приближённую оценку рассчитывают по формуле:

r = ;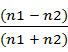

где n1 суммарное количество точек в I и III, n2 = суммарное количество точек в II и IV.

I = 4 II = 8 III = 7 IV = 5

r = 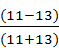= -0.08

Далее используя вычисленные компьютером исходные данные (Хср, Yср, дисперсии Dx, Dy, и их ковариацию cov(x,y)) вычисляем значение коэффициента корреляции r и параметры уравнений линейной регрессии попутного компонента по основному и основного компонента по попутному.

Вычисляем по следующим формулам:

Исходные данные:

Хср = 36,75

Yср = 153,13

Dx = 157,27

Dy = 645,61

cov (x, y) = 163,86

Формулы:

r = cov(x, y)/√Dx * Dy = 163,86/√157,27* 645,61= 0,51

b = cov(x, y)/Dx = 163,86/157,27= 1,04

a = Yср – b * Xср = 153,13– (-0.08) * 36,75= 150.19

d = cov(x, y)/ Dy = 163,86/645,61= 0.25

c = Хср – d * Yср = 36,75– (0.25) * 153,13= -1.5

y =150.19+1.04x x = -1.5+0.25y

Строим линии регрессии на корреляционном поле.