Прямой, обратный и дополнительный коды
Позиционные системы счисления
Под системой счисления понимается способ представления любого числа посредством некоторого алфавита символов, называемых цифрами.
Огромными преимуществами в наглядности представления чисел и в простоте выполнения арифметических операций обладают позиционные системы счисления. Этим объясняется то выдающееся значение для развития вычислений, которое имело создание арабами позиционной десятичной системы счисления, используемой нами в повседневной жизни.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, определяющееся позицией цифры в последовательности цифр, изображающей число. Это значение меняется в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону. Помимо десятичной системы существуют другие позиционные системы. 2-я, 8-ричная, 16-ричная нашли применение в вычислительной технике.
Римская система счисления - непозиционная,так как символы I,V,X свое значение сохраняют независимо от позиции, а значение числа получается сложением входящих символов, напримерXX1 – 21, 1XX – 19, XV – 40, VX – 60, VXX1 – 71.
В двоичной системе любое число может быть, представлено соответствующей последовательностью двоичных цифр
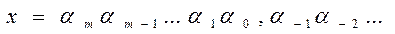
где αi могут быть либо 0, либо 1. Эта запись соответствует сумме степеней числа 2, взятых с указанными в ней коэффициентами:
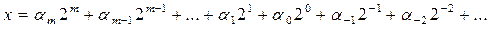
Например, двоичное число
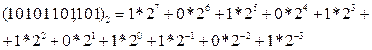
как следует из приведенного разложения его по степеням числа 2, соответствует десятичному числу: 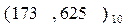
Двоичная арифметика
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения:
| Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
| 0+0=0 0+1=1 1+0=1 1+1=0 + +единица переносится в старший разряд | 0-0=0 1-0=1 1-1=0 0-1=1 + +единица занимается из старшего разряда | *0=0 0*1=0 1*0=0 1*1=1 |
Прямой, обратный и дополнительный коды
При проектировании вычислительных устройств необходимо решить вопрос о способе представления в машине положительных и отрицательных чисел и о признаке переполнения разрядной сетки. Указанный вопрос решается применением специальных колов для представления чисел. При помощи этих кодов операция вычитания (или алгебраического сложения) сводится к арифметическому сложению. В результате упрощаются арифметические устройства машин.
Для представления двоичных чисел в машине применяют прямой, обратный и дополнительный коды. Во всех этих кодах предусматривается дополнительный разряд для представления знака числа, причем знак «+» кодируется цифрой 0, а знак « — » - цифрой 1.
Положительные числа в прямом, обратном и дополнительном кодах имеют один и тот же вид, а отрицательные — различный.
