Основные теоремы о пределах

Пример 4.

1. Составить список элементов множеств, заданных характеристическими свойствами: 1) А= {x : x² – 8 x+15=0 }; 2) А = { x: x∈N,

–11<x≤–3}.

2. Доказать, что если А= {x : x² – 7 x+6=0 } и В={1, 6}, то А=В.

3. Описать множества точек М плоскости, таких, что: 1) {М: │ОМ │= R};

2) {М: │ОМ │≤ R}; 3) {М: │АМ │= │ВМ │}, где А и В — заданные точки.

4. Какая разница в записях А⊂В и А∈В?

5. Доказать, что {{1, 2}, {2, 3}}≠{1, 2, 3}.

6. Верно ли, что {1, 2}∈ {{1, 2, 3}, {1, 3}, 1, 2}? Верно ли, что {1, 2}⊆{{1, 2, 3}, {1, 3}, {1, 2}?

7. Привести примеры таких множеств А, В и С, что: 1) А∈В, В∈С, А 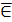С ;

2)А⊆В, В⊆С, А⊆С; 3) А∈В, А⊂В.

8. Является ли множество, состоящее из числа 0, пустым?

9. Доказать справедливость соотношения: ≠ { }.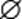

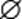10. Доказать, что существует только одно множество, не имеющее элементов.

11. Найти все подмножества множеств: 1) 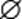; 2) { }; 3) {1, 2}; 4) {a, b, c, d}.

12. Доказать, что если А⊆В, В⊆А, то А=В, и обратно, если А=В, то А⊆В, В⊆А.

§2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ

Объединением А 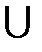В множеств А и В называется множество, состоящее из элементов, входящих в множества А и В, и только из них, т.е. А 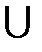В ={x : x∈A или x∈В}.

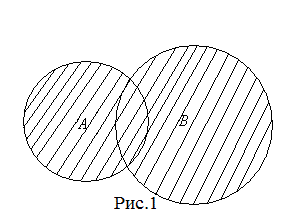Если один и тот же элемент содержится и во множестве А и во множестве В, то в их объединение он входит только один раз. Схематически объединение множеств А и В изображено на рис.1.

Объединением 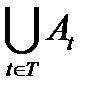множеств A_t (t∈T) называется множество, состоящее из элементов, входящих в множества A_t (t∈T), и только из них (здесь предполагается, что индекс t пробегает все значения из некоторого множества T.

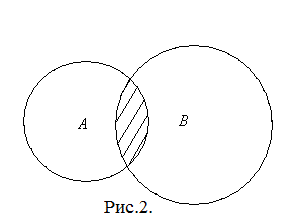
Пересечением А В множеств А и В называется множество, состоящее из элементов, принадлежащих как множеству А, так и множеству В, и только из них, т.е. А В={x : x∈A и x∈B}. Схематически пересечение множеств А и В изображено на рис.2.

Пересечением 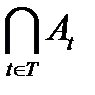множеств A_t (t∈T) называется множество, состоящее из элементов, принадлежащих множествам A_t (t∈T), и только их них.

Если пересечение множеств не является пустым, то множества называют пересекающимися.

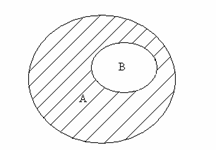Разностью А∖В множеств А и В называется множество, состоящее из элементов множества А, не входящих в множество В, и только из них, т.е.

А∖В={ x : x∈А и x∈В }. Схематически разность множеств А и В изображена на рис.3.

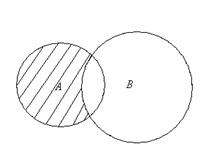
Рис.3.

Разность J∖B, где J —универсальное множество, называется дополнением множества В и обозначается .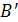

Пример 1.Доказать тождество 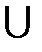А А= А А=А.

Пример 2.Доказать, что если А_t⊆B для всех t∈T, то 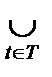A_t⊆В.

Пример 3.Доказать, что если А⊆В 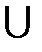С, то А 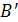⊆С, и обратно.

Пример 4.В каком из отношений (X⊂Y, X⊃Y, X=Y) находятся множества X и Y, если: 1) X= А 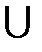(В∖С), Y=(А 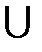В) ∖ (А 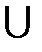С); 2) X=(А В) ∖ С; Y=(А∖С) (В ∖С); 3) X= А ∖ (В 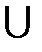С), Y=(А∖В) 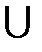(А∖С).

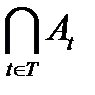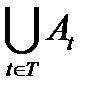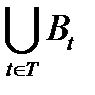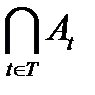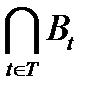Пример 5.Доказать, что: 1) для всех t∈T, В⊆А_t , то В⊆ ; 2) если для всех t∈T А_t⊆В_i, то ⊆ и ⊆ ; 3) 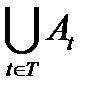∖ 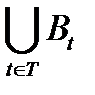= 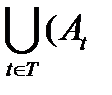∖ В_t);

4) 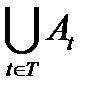есть наименьшее множество, включающее все множества А_t; 5) 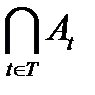есть наименьшее множество, содержащееся во всех множествах А_t.

§3. ЭКВИВАЛЕНТНОСТЬ МНОЖЕСТВ

Если каждому элементу множества А по какому-то правилу можно сопоставить один и только один элемент множества В и обратно каждому элементу множества В можно сопоставить один и только один элемент множества А, то говорят, что между множествами А и В установлено взаимно-однозначное взаимодействие.

Множества А и В называются эквивалентными, А ~ В, если между ними можно установить взаимно-однозначное соответствие, в противном случае множества называются неэквивалентными, А 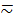B .

Для установления факта эквивалентности двух множеств достаточно указать какое-либо правило установления их взаимно-однозначного соответствия.

Отношение эквивалентности между множествами обладает свойствами:

1) рефлексивности —A ~ A;

2) симметричности —если A ~ B, то B ~ A;

3) транзитивности —если A ~ B, а В ~ С, то A ~ С.

Мощностью множества А называется класс всех множеств, эквивалентных множеству А, т.е. мощность есть то общее, чем характеризуются все эквивалентные между собой множества.

Если А 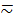B и А ~ B₁ ⊂B, то мощность множества А считается меньшей мощности множества В.

Непустое множество А называется конечным, если существует такое число

n∈N, что А ~ {1, 2, …, n}. В этом случае говорят, что множество А имеет мощность, равную n, или что оно имеет n элементов.

Пустое множество также считается конечным, и его мощность равна нулю.

Множество, не являющееся конечным, называется бесконечным.

Множество А, эквивалентное множеству Nнатуральных чисел, называется счетным, и его мощность обозначается символом 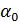. Для установления счетности множества достаточно указать правило пересчета его элементов всеми натуральными числами.

Множество, эквивалентное множеству Rвещественных чисел, называется множеством мощности континуума, и его мощность обозначается символом с.

Мощности произвольных множеств называются кардинальными числами. Мощности конечных множеств выражаются натуральными числами (или нулем для пустого множества), т.е. кардинальные числа для конечных множеств —натуральные числа (или нуль для пустого множества).

Над мощностями (кардинальными числами) выполнимы только две операции — сложение и умножение. Суммой 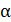+β двух мощностей α и β множеств А и В, не имеющих общих элементов, называется мощность множества С, являющегося объединением множеств А и В. Произведением αβ двух мощностей α и β множества А и В называется мощность множества С, элементами которого являются все упорядоченные пары, составленные из элементов множеств А и В.

Действия над мощностями:

1) коммутативны —α+β=β+α, αβ=βα;

2) ассоциативны —(α+β) + γ= α + (β+ γ), (αβ) γ= α(βγ);

3) дистрибутивны —(α+β) γ= αγ +βγ.

Пример 1.Можно ли сказать, что если A = B, то A ~ B ?

Пример2.Установить взаимно-однозначное соответствие между множествами А = {x : x∈R, 0 ≤ x <1}и В = {y : y∈R, a ≤ y <b}.

Пример 3.Доказать равномощность: 1) множества точек окружности и множества точек контура квадрата; 2) множества точек окружности без одной точки и множества точек прямой; 3) множества точек сферы без одной точки и множества точек плоскости.

Пример 4.Доказать, что для любого бесконечного множества А можно выделить его собственное подмножество А₁ такое, что А₁ ~ A.

Пример 5.Доказать, что: 1) конечное множество не эквиваленто никакому своему собственному подмножеству; 2) два конечных множества эквивалентны тогда и только тогда, когда они содержат одинаковое количество элементов.

Пример 6.Доказать, что: 1) всякое подмножество конечного множества конечно; 2) объединение конечного числа конечных множеств конечно.

Пример 7. Доказать, что не существует множества, содержащего все множества.

Пример 8. Доказать, что из всякого бесконечного множества можно выделить счетное подмножество.

Пример 9.Доказать, что среди всех бесконечных множеств счетные множества имеют наименьшую мощность.

Пример 10.Доказать, что всякое подмножество счетного множества счетно или конечно.

Пример 11.Доказать, что множество нечетных чисел счетное.

Пример 12.Доказать, что множество целых неотрицательных чисел счетное.

Пример 13. Доказать, что множество целых чисел, делящихся на 10, счетное.

Пример 14.Доказать, что множество рациональных чисел счетное.

Пример 15.Доказать, что множество точек плоскости с целыми координатами счетное.

Пример 16.Доказать, что если из множества мощности континуума удалить конечное число или счетное подмножество, то оставшееся множество будет множеством мощности континуума.

Пример 17.Определить мощность множества иррациональных чисел.

Пример 18.Доказать, что кардинальных чисел бесконечно много и среди них нет наибольшего.

Пример 19.Доказать, что 2+2=4, 2∙2=4.

§4. ПОНЯТИЕ ФУНКЦИИ.

1.Области определения и значений. График функции. Сложная и обратная функции.

Если даны числовые множества X={x}и Y={y}и по некоторому закону f каждому элементу x∈X поставлен в соответствие один и только один элемент

y∈Y , то говорят, что на множестве X задана функция y=f(x), x называют аргументом функции, y —ее значением.

Через f(a) или y(a) обозначается то значение y, которое соответствует значению x=a.

Множество X называется областью определения, или областью существования функции, множество Y —областью изменения функции, или областью ее значений.

Для лучшего понимания определения функции следует познакомиться с элементами входящие в это определение.

Df. Величина «у» называется функцией переменной величины «х» если каждому значению переменной х из указанной её области изменения D(f) соответствует одно или несколько определенных значений «у».

Записывают это так: 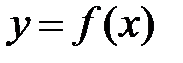х – аргумент (независимая переменная). Если каждому значению «х» соответствует одно определенное значение у, то функцию «у» называют однозначной.

Если аргумент «х» может принимать только значения действительных чисел, то функция у называется функцией действительной переменной х.

Если же каждому значению «х» соответствует несколько определенных значений у (два, три и т.д.) то функция «у» называется многозначной (двузначной, трехзначной и т.д.)

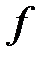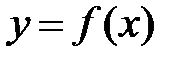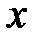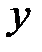Буква , входящая в равенство в отличии от букв « » и « » обозначает не переменную величину, а то правило (закон), по которому устанавливается соответствие между « 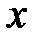» и « » .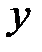

В частности, буква 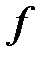может обозначать совокупность математических операций, которые нужно произвести над аргументом « 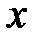» чтобы получить соответствующее значение « 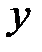», и указывать последовательность их выполнения.

Символ 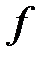называют характеристикой функции.

Буква 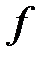может обозначать не только математические операции и последовательность их выполнения, а и правило сформулированное любым способом (словами, таблицей, графиком и т.д.) по которому каждому значению « 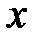» можно найти соответствующее значение « ».

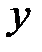Если функция 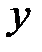задана формулой 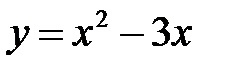, то роль 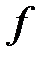здесь играет предложение:

«Чтобы получить значение 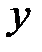, зная значения х нужно из квадрата числа 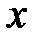вычесть утроенное это число».

Если функция y=f(x) задана аналитически (при помощи формулы), то под областью Х ее определения понимается множество тех вещественных значений аргумента x, при которых аналитическое выражение f(x) имеет смысл, т.е. выполнимы все действия, указанные в задании функции. Нахождение области определения функции, как правило, сводится к решению некоторой системы неравенств, содержащих аргумент x. Нахождение области Y значений функции производится либо преобразованием данного аналитического выражения к виду, содержащему функции, области изменения которых известны, либо к нахождению области определения функции, обратной данной.

Функция, заданная разными формулами для различных значений аргумента, называется кусочно-аналитической. Например, 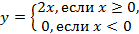—кусочно-аналитическое задание функции (эта функция может быть задана и одной формулой y=x+│x│). Функция знака числа x, y=sign x, задается так:

y=

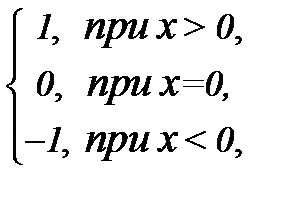
ее график изображен на рис.1.

Если задано уравнение F (x, y)=0, связывающее функцию y и аргумент x, то говорят, что функция y задана неявно. Например, уравнение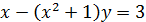

является неявным заданием функции y. Если разрешить это уравнение относительно y, то получим 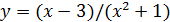—явное аналитическое задание функции y.

З а м е ч а н и е. Обычно выражение y через x при неявном задании функции не так просто, как в приведенном примере. Но при решении многих задач и не требуется выражать функцию явно.

Рис.1

Графиком функции y=f(x) называется геометрическое место точек ( x, y ) плоскости, координаты x и y которых связаны соотношением y=f(x) и x принадлежит области определения данной функции. Обычно графиком функции является некоторая кривая на плоскости, а само уравнение y=f(x) называют уравнением этой кривой. Напомним способы построения графиков функций, используя функции, графики которых известны (таблица).

Пусть функция z = φ(y) определена на множестве Y —множество значений некой функции y=f(x) с областью определения X; тогда переменная z является функцией от x на множестве X : z = φ(f(x)).

Функция z = φ(f(x)), аргументом которой является другая функция (точнее, функция другого аргумента), называется сложной функцией переменной x; функция y=f(x) называется внутренней, а функция z = φ(y) —внешней. Говорят также, что сложная функция является суперпозицией этих функций или что задана композиция двух функций.

Например, функции 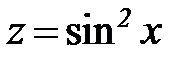, 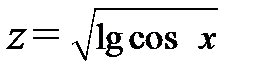являются сложными функциями. Функция 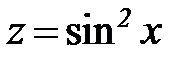может быть представлена как 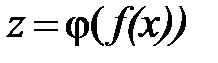, где 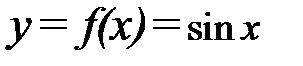—внутренняя функция, а 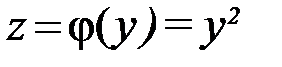—внешняя. Пример сложной функции 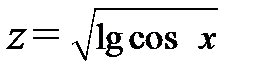демонстрирует «трехступенчатую» функциональную зависимость функции z от аргумента x: z=g(φ(f(x))), где t = f(x) =cos x —тригонометрическая функция; y=φ(t) = lg t —логарифмическая функция; z=g(y) = 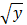—степенная функция.

Функция y=f(x) с областью определения X и множеством значений Y называется взаимно-однозначной, если для любых х₁ и х₂ из области ее определения Х из неравенства х₁≠х₂ следует, что f(x₁) ≠ f(x₂), т.е. различным значениям аргумента соответствуют различные значения функции.

Примером взаимно-однозначных функций являются строго монотонные функции. Для функций, не являющихся взаимно-однозначными на всей области определения, часто удается выделить промежутки, на которых они взаимно-однозначны. Например, функция y=x² не являются взаимно-однозначной для всех x (для x≠0 различным значениям аргумента x и –x соответствуют равные значения функции y=x²), но на промежутках (–∞; 0] и [0; +∞) она взаимно-однозначна.

Функция, определенная на множестве Y (множестве значений взаимно-однозначной функции y=f(x)), ставящая в соответствие каждому y∈Y то значение x∈X (из области определения функции y=f(x)), для которого y=f(x), называется обратной к функции y=f(x).

Для нахождения функции (если она существует), обратной данной y=f(x), необходимо выразить x через y : x= φ(y), а затем записать полученную функцию в обычном виде : y=f(x). Например, обратной для функции y=2х+4 является функция y= х–2.

Условия существования обратной функции приведены в § 2 главы III.

Область определения обратной функции совпадает с множеством значений исходной функции, и наоборот, множество значений обратной функции совпадает с областью определения исходной функции.

Графики прямой и обратной функций симметричны относительно прямой y=x.

Суперпозиция взаимно-обратных функций y=f(x) и x=f ^-1(y) является тождественной функцией: f(f ^-1(y)) = y; f(f ^-1(x)) = x.

Пример 1.1) Выразить объем цилиндра, вписанного в шар радиусом R, как функцию его высоты h.

2) Имеются два куска сплава меди с серебром. В первом куске содержится p% меди, во втором —q% меди (p<q).

Задание функции	Способ построения ее графика	График
1.   y = f(x)+A	Y X A y=f(x) y=f(x)+A, A>0 Рис.2 Параллельный перенос (сдвиг) графика функции y=f(x) вдоль оси OY на |A| единиц вверх, если А>0, или вниз, если A<0. (рис.2.)
2. y = f(x+a)	Рис.3 Y X |a| y=f(x) y=f(x+a), a<0 Параллельный перенос графика функции y = f(x) вдоль оси OX на |a| единиц влево, если a>0, или вправо, если a<0. (рис.3.)
3. y=kf(x)	X Y y=f(x) y=kf(x), k>1 Рис.4 y=f(x) y= –f(x), k= –1 X Y Рис.5 Y X y=f(x)   y= kf(x), k<–1   Рис.6 Растяжение вдоль оси OY в k раз, если k>1, или сжатие в 1/k раз, если 0<k<0 (рис.4). Симметричное отображение графика y=f(x)относительно оси OX, если k=–1(рис.5). Растяжение в |k| раз и симметричное отображение относительно оси OX при k<–1; сжатие в 1/|k| раз и симметричное отображение относительно оси OX при –1<k<0 (рис.6).
4. y=|f(x)|	Рис.7 X Y y=f(x)   y=|f(x)| Оставить без изменений часть графика y=f(x), лежащую выше оси OX, а остальную часть графика (расположенную ниже оси ОХ) отобразить относительно оси абсцисс (рис.7).
5. y=f (kx)	Рис.8 Y X y=f(x)   y=f(kx), k<1   Сжатие графика функции y=f(x) вдоль оси OX в k раз, если k>1, растяжение вдоль оси OX в 1/k раз, если 0<k<1 (рис.8), симметричное отображение относительно оси OY, если k= –1.(рис.9) Y y=f(-x) y=f(x) Рис.9 X
6. y=f (|x|)	y=f(x) y=f(|x|) Y X Рис.10 Отбросить часть графика y=f(x), лежащую в левой полуплоскости; остальную часть графика (лежащую в правой полуплоскости) сохранить и, кроме того, отобразить относительно оси OY (рис.10).

При переплавке х кг первого сплава с у кг второго получили сплав, содержащий r % меди. Выразить зависимость у от х.

2.Четные и нечетные функции.

Функция y=f(x)называется четной, если для всех х из области ее определения выполняется равенство f( –x)= f(x).

Функция y=f(x) называется нечетной, если для всех х из области ее определения выполняется равенство f( –x)= – f(x).

Функции, не четные и не нечетные, называются функциями общего вида.

Свойства четных и нечетных функций.

1. Область определения четной и нечетной функций симметрична относительно начала координат.

2. График четной функции симметричен относительно оси координат.

3. График нечетной функции симметричен относительно начала координат.

4. Сумма, разность, произведение и частное двух четных функций с одной и той же областью определения (знаменатель дроби при этом должен быть отличен от нуля) также являются четными функциями.

5. Сумма и разность двух нечетных функций (с одной областью определения) есть нечетные функции.

6. Произведение и частное двух нечетных функций являются четными функциями.

7. Произведение и частное четной и нечетной функций есть нечетные функции.

При построении графиков четных и нечетных функций достаточно построить только ту часть графика, которая лежит в правой полуплоскости (при х≥0), а затем отобразить ее симметрично относительно оси ординат (для четной функции) или относительно начала координат (для нечетной функции).

Пример 2.Установить, какие из следующих функций являются четными, нечетными и какие — функциями общего вида.

1) y = 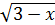, 2) y =x² + |x|, 3) y =tg²x – cos x, 4) y = lg 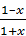, 5) y = x ,

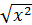6) y = 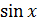+ 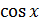, 7) y = 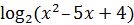, 8) y = (2^x –1)/( 2^x +1), 9) доказать свойство 5.

Решение 4): Область определения функции y = lg 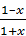, симметрична относительно начала координат: x∈(–1,1).При этом f (–x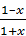)= lg =lg = – lg 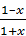= – f (x), следовательно, функция нечетная.

3. Периодические функции.

Функция y=f(x) называется периодической, если существует такое число Т>0 (не зависящее от х), что:

1) х+Т и х–Т также входят в область определения функции f(x);

2) для всех х из области определения функции выполняется равенство: f(x+Т)= f(x);

3) среди всех Т есть наименьшее.

Это наименьшее число Т называется периодом функции.

Свойства периодических функций.

1. Область определения периодической функции симметрична относительно начала координат.

2. Для периодической функции y=f(x) справедливо равенство f(x+kТ) = f(x), где Т — период функции, k∈Z; в частности, f(x–Т) = f(x).

3. Если функция y=f(x) периодическая с периодом Т, то функция y=f(ax) также периодическая с периодом Т/|a| (при a≠0).

4. Если функция y=f(x) периодическая с периодом Т, то функция y=f(x+a) также периодическая с периодом Т.

При построении графика периодической функции достаточно построить часть графика на интервале, равном одному периоду, а затем продолжить его на всю область определения функции.

Пример 3.Исследовать на периодичность следующие функции:

1) y=x²+x–1; 2) y=2; 3)y=sin x+1; 4) y=sin x – cos x; 5)y=sin 2x – 2tg ; 6)y=cos²x; 7)y=x–|x|.

4. Возрастающие, убывающие и ограниченные функции.

Функция y=f(x), определенная на множестве Х, называется возрастающей, если для любых х₁, х₂ множества Х из неравенства х₁ <х₂ следует, что:

f(x₁)< f(x₂) (1)

т.е. функция y=f(x) называется возрастающей, если большему значению ее

Y

x2

x1

X

f(x1)

f(x2)

аргумента из области определения соответствует большее значение функции (рис.11)

Y

X

x2

x1

f(x2)

f(x1)

Рис.11 Рис. 12

Функция y=f(x), определенная на множестве Х, называется убывающей, если для любых х₁, х₂ множества Х из неравенства х₁ <х₂ следует, что:

f(x₁)< f(x₂), (2)

т.е. функция y=f(x) называется возрастающей, если большему значению ее аргумента из области определения соответствует меньшее значение функции (рис. 12).

Возрастающие и убывающие функции называются строго монотонными.

Если в определении возрастающей функции неравенство (1) заменить на нестрогое f(x₁)≤ f(x₂), то такая функция называется неубывающей ( рис.13). Если в определении убывающей функции неравенство (2) заменить на нестрогое f(x₁)≥ f(x₂) , то такая функция называется невозрастающей (рис. 14).

Возрастающие, убывающие, невозрастающие, неубывающие функции называются монотонными функциями.

X

Y

X

Y

Рис.13 Рис.14

Свойства монотонных функций:

1. Сумма двух возрастающих (убывающих) функций есть функция возрастающая (убывающая).

2. Если функция y=f(x) возрастающая (убывающая), то функция y= –f(x) убывающая (возрастающая).

3. Если функция y=f(x) возрастающая (убывающая), то функция y= 1 / f(x)

убывающая (возрастающая) (f(x)≠0).

4. Суперпозиция двух монотонно возрастающих (убывающих) функций есть

монотонно возрастающая функция.

5. Суперпозиция двух функций, из которых одна монотонно возрастающая, а

другая монотонно убывающая, является монотонно убывающей функцией.

Функция y=f(x), определенная на множестве Х, называется ограниченной сверху на данном множестве, если существует число М такое, что f(x) ≤ М для любого х∈Х.

Функция y=f(x), определенная на множестве Х, называется ограниченной снизу, если существует число m такое, что f(x) ≥ m для любого х∈Х.

Функция y=f(x), определенная на множестве Х, называется ограниченной на данном множестве, на данном множестве, если существует число N >0такое, что |f(x)| ≤ N для любого х∈Х. Ясно, что функция y=f(x) является ограниченной тогда и только тогда, когда она ограничена и сверху, и снизу.

Сумма и произведение ограниченных функций являются также ограниченными функциями.

Пример 4.Исследовать на монотонность следующие функции:

1) y = sin x на отрезке [–π/2, π/2 ]; 2) y = arctg (x²–2x+3);

2) y = (x²+4x+6) ln (x²+4x+6); 4) y = (1–x²)/x; 5) доказать свойство 1 для монотонно убывающих функций

5. Функция натурального аргумента (числовая последовательность).

Частным случаем функции является функция натурального аргумента y=f(n), (n∈N), которая обычно обозначается x_n и называется числовой последовательностью. Областью определения такой функции является множество N натуральных чисел, а каждое значение x_n называется членом последовательности. Значению аргумента n соответствует число x_n , стоящее на месте с номером n в этой последовательности. Последовательность считается заданной, если указано правило, по которому каждому значению аргумента n (натуральному числу) поставлено в соответствие единственное значение x_n. Число x_n называется общим членом последовательности. Для задания последовательности достаточно знать ее общий член, ибо, зная номер члена последовательности, всегда можно найти и сам член. Так, если x_n= 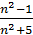— общий член последовательности, то ее первые члены равны 0, 3/9, 8/14, …, а, например, десятый член x₁₀=99/105.

Если существует число m (М) такое, что для всех (n∈N) справедливо неравенство x_n ≥m (x_n ≤ M).

Последовательность x_n называется ограниченной, если существует число L такое, что справедливо неравенство |x_n| ≤ L.

Последнее определение равносильно тому, что последовательность x_n ограничена и снизу и сверху.

Последовательность x_n называется возрастающей (неубывающей), если для всех (n∈N) справедливо неравенство x_n+1 ≥ x_n, и убывающей (невозрастающей), если для всех (n∈N) справедливо неравенство x_n+1 ≤ x_n. Если верны соответственно строгие неравенства x_n+1 > x_n или x_n+1 < x_n, то последовательности называются строго возрастающей или строго убывающей.

Пример 5.1) Найти формулу общего члена последовательности x_n , если x₁=1, а x_n= x_n-1 + d.

3) Доказать, что последовательность x_n= 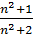ограничена.

4) Доказать, что последовательность x_n = lg n – lg (n – 1) монотонна, начиная с некоторого номера n(n >1).

5) Найти наибольший член последовательности x_n = n²/2ⁿ.

6) Найти наибольший член последовательности x_n = n² – 5n +1.