Ереход к физическим переменным
Для записи ММ в реальных физических величинах производят обратный переход от стандартизированного масштаба к натуральному. Это можно сделать с помощью соотношения (2.2). После чего записывают окончательный вид модели.
3. Индивидуальные задания для выполнения лабораторной работы
Задания выполняются в соответствии с индивидуальными вариантами, приведенными в Приложении Г. Номер варианта соответствует номеру студента в списке группы.
Вариант задания представляет собой результаты ПФЭ типа 22. В ходе эксперимента в каждой точке факторного пространства проводились три параллельных опыта. Порядок проведения опытов соответствует матрице эксперимента, представленной в таблице 2.2.
В ходе выполнения индивидуального задания требуется по предложенным экспериментальным данным построить регрессионные линейные модели и провести регрессионный анализ построенных моделей моделей. Для этого необходимо:
- построить матрицу планирования экспериментов;
- проверить воспроизводимость опытов;
- рассчитать оценки коэффициентов регрессионного уравнения;
- проверить адекватность полученной модели;
- провести анализ результатов и сделать выводы.
4. СОДЕРЖАНИЕ ОТЧЕТА О ВЫПОЛНЕНИИ лабораторной работы
Отчет о выполненной работе должен содержать:
1. Цель работы.
2. Постановку задачи.
3. Матрицу планирования эксперимента.
4. Результаты проверки воспроизводимости опытов.
5. Результаты расчетов коэффициентов регрессионных моделей и проверки из статистической значимости.
6. Результаты проверки адекватности полученной модели исходным экспериментальным данным.
7. Выводы и предложения о ходе дальнейших исследований, составленные на основании анализа регрессионных моделей.
5. Пример выполнения задания
Требуется исследовать влияние технологических факторов (номиналов резисторов R1 и R2) в интегральной транзисторно-транзисторной логической схеме на значение средней потребляемой мощности P=f(R1, R2). Номинальные значения факторов: R1=7кОм, R2=3кОм, область изменения факторов соответственно [5;9] и [2;4] кОм. Функцию f(R1, R2) будем искать в виде линейной модели (2.1).
Составим ПФЭ для четырех серий опытов при интервалах варьирования для R1 — 0,4кОм, R2 — 0,2кОм. Для стандартизации масштабов факторов вычислим значения нижнего и верхнего уровня согласно соотношению (2.2) и сведем результаты в таблицу 5.1.
Таблица 5.1 — Условия проведения ПФЭ.
| Характеристика плана | Стандартный масштаб xi | Натуральный масштаб | |
| x1=R1, кОм | x2=R2, кОм | ||
| Нулевой уровень | |||
| Верхний уровень | +1 | 7,2 | 3,1 |
| Нижний уровень | -1 | 6,8 | 2,9 |
Составим матрицу эксперимента с учетом рандомизации опытов. В таблице 5.2 представлены результаты параллельных опытов и вычислены среднее значение отклика и дисперсия для каждой точки факторного пространства соответственно соотношениям (2.3) и (2.4).
Проведем анализ воспроизводимости опыта на основе критерия Кохрена в соответствии с (2.5): Gрасч=0,485, табличное значение критерия определяем при уровне значимости α=0,05 и степенях свободы γ1=m-1=4, γ2=N=4, получаем Gтабл(α;γ1;γ2)=0,630. Так как Gрасч< Gтабл, опыт является воспроизводимым, и его результаты можно использовать для оценки коэффициентов регрессионного уравнения.
Таблица 5.2 — Результаты эксперимента.
| № | x0 | x1 | x2 | y1 | y2 | y3 | y4 | y5 | ycp | s2yi |
| -1 | -1 | 6,54 | 6,29 | 6,51 | 6,42 | 6,56 | 6,46 | 0,02 | ||
| -1 | 6,57 | 6,37 | 6,33 | 6,21 | 6,10 | 6,32 | 0,04 | |||
| -1 | 6,28 | 6,37 | 6,37 | 6,15 | 6,46 | 6,33 | 0,02 | |||
| 6,21 | 6,00 | 6,01 | 6,07 | 6,13 | 6,08 | 0,01 |
В соответствии с расчетным соотношением (2.6) можно определить коэффициенты регрессионной модели.
Для анализа значимости коэффициентов необходимо вычислить погрешности определения коэффициентов модели и расчетное значение t – критерия Стьюдента на основании соотношений (2.7) — (2.9). Результаты расчетов в таблице 5.3.
Таблица 5.3 — Результаты анализа значимости коэффициентов.
| b0 | b1 | b2 | |
| коэффициенты регрессионной модели | 6,296 | -0,097 | -0,093 |
| погрешности определения коэффициентов | 0,011 | 0,020 | 0,020 |
| tрасч | 188,93 | 2,92 | 2,78 |
| вывод | зн | зн | зн |
Для принятия решения о значимости коэффициентов уравнения регрессии расчетное значение критерия Стьюдента tрасч сравнивается с табличным значением. Табличное значений критерия Стьюдента tтабл выбирается при уровне значимости α=0,05 и степени свободы γ=N(m-1)=16, tтабл=2,12. Неравенство tрасч >tтабл выполняется для всех коэффициентов ММ, поэтому они все считаются значимыми и включаются в модель.
Проверка адекватности построенной модели выполняется в соответствии с критерием Фишера (2.11). Согласно выражению (2.9) дисперсия воспроизводимости равна s2воспр=0,022, остаточная дисперсия в соответствии с (2.10) составляет s2ост= 0,036, Расчетное значение критерия Фишера (2.11) равно Fрасч=1,63. Табличное значений критерия Фишера Fтабл выбирается при уровне значимости α=0,05 и степенях свободы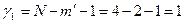 
и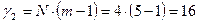 
, Fтабл=4,49. Неравенство Fрасч< Fтабл выполняется, поэтому построенная регрессионная модель считается адекватной экспериментальным данным.
Перейдем от кодированных значений факторов к натуральному исчислению в соответствии с выражением (2.2) и условиями проведения эксперимента в таблице 2.6:
P=12,484-0,487R1-0,925R2. (2.12)
Таким образом, выражение (2.12) представляет характер изменения средней потребляемой мощности P интегральной транзисторно-транзисторной логической схемы в области изменения номиналов резисторов 6,8≤R1≤7,2 кОм, 2,9≤R2≤3,1 кОм.
5. Контрольные вопросы
1. В чем сущность планирования эксперимента? Поясните разницу между активным и пассивным экспериментом.
2. Какие задачи решает теория планирования эксперимента?
3. Что такое факторы и какие требования к ним предъявляются? Как выбрать уровни варьирования факторов?
4. Какие требования предъявляются к факторам?
5. В чем сущность ПФЭ и какие ММ он позволяет исследовать?
6. Какую область описывает уравнение регрессии, полученное с помощью ПФЭ и в каких границах его можно использовать?
7. В чем сущность и цели стандартизации масштаба факторов?
8. Как составляется и какими свойствами обладает МП ПФЭ?
9. Каков порядок постановки опытов при ПФЭ?
10. Как проверить воспроизводимость опытов?
11. Как рассчитать оценки коэффициентов регрессионного уравнения?
12. Как проверить статистическую значимость оценок коэффициентов регрессии?
13. Как проверить адекватность полученной ММ?
14. Как перейти к исходным физическим переменным?
Библиографический список
1. Космин В.В. Основы научных исследований: Учебное пособие для магистров / В.В. Космин. — М.: РИОР: ИНФРА-М, 2013. — 213 с.
2. Сидняев Н.И. Теория планирования эксперимента и анализ статистических данных. / Н.И. Сидняев — М.: Юрайт-Издат, ООО, 2012. — 399с.
Приложение А
Распределение Фишера.
Значения F–критерия Фишера при 5%-ном уровне значимости
| ν1 ν2 | ¥ | ||||||||
| 164.4 | 199.5 | 215.7 | 224.6 | 230.2 | 234.0 | 244.9 | 249.0 | 254.3 | |
| 18.5 | 19.2 | 19.2 | 19.3 | 19.3 | 19.3 | 19.4 | 19.4 | 19.5 | |
| 10.1 | 9.6 | 9.3 | 9.1 | 9.0 | 8.9 | 8.7 | 8.6 | 8.5 | |
| 7.7 | 6.9 | 6.6 | 6.4 | 6.3 | 6.2 | 5.9 | 5.8 | 5.6 | |
| 6.6 | 5.8 | 5.4 | 5.2 | 5.1 | 5.0 | 4.7 | 4.5 | 4.4 | |
| 6.0 | 5.1 | 4.8 | 4.5 | 4.4 | 4.3 | 4.0 | 3.8 | 3.7 | |
| 5.5 | 4.7 | 4.4 | 4.1 | 4.0 | 3.9 | 3.6 | 3.4 | 3.2 | |
| 5.3 | 4.5 | 4.1 | 3.8 | 3.7 | 3.6 | 3.3 | 3.1 | 2.9 | |
| 5.1 | 4.3 | 3.9 | 3.6 | 3.5 | 3.4 | 3.1 | 2.9 | 2.7 | |
| 5.0 | 4.1 | 3.7 | 3.5 | 3.3 | 3.2 | 2.9 | 2.7 | 2.5 | |
| 4.8 | 4.0 | 3.6 | 3.4 | 3.2 | 3.1 | 2.8 | 2.6 | 2.4 | |
| 4.8 | 3.9 | 3.5 | 3.3 | 3.1 | 3.0 | 2.7 | 2.5 | 2.3 | |
| 4.7 | 3.8 | 3.4 | 3.2 | 3.0 | 2.9 | 2.6 | 2.4 | 2.2 | |
| 4.6 | 3.7 | 3.3 | 3.1 | 3.0 | 2.9 | 2.5 | 2.3 | 2.1 | |
| 4.5 | 3.7 | 3.3 | 3.1 | 2.9 | 2.8 | 2.5 | 2.3 | 2.1 | |
| 4.5 | 3.6 | 3.2 | 3.0 | 2.9 | 2.7 | 2.4 | 2.2 | 2.0 | |
| 4.5 | 3.6 | 3.2 | 3.0 | 2.8 | 2.7 | 2.4 | 2.2 | 2.0 | |
| 4.4 | 3.6 | 3.2 | 2.9 | 2.8 | 2.7 | 2.3 | 2.1 | 1.9 | |
| 4.4 | 3.5 | 3.1 | 2.9 | 2.7 | 2.6 | 2.3 | 2.1 | 1.9 | |
| 4.4 | 3.5 | 3.1 | 2.9 | 2.7 | 2.6 | 2.3 | 2.1 | 1.9 | |
| 4.3 | 3.4 | 3.1 | 2.8 | 2.7 | 2.6 | 2.2 | 2.0 | 1.8 | |
| 4.3 | 3.4 | 3.0 | 2.8 | 2.6 | 2.5 | 2.2 | 2.0 | 1.7 | |
| 4.2 | 3.4 | 3.0 | 2.7 | 2.6 | 2.5 | 2.2 | 2.0 | 1.7 | |
| 4.2 | 3.3 | 3.0 | 2.7 | 2.6 | 2.4 | 2.1 | 1.9 | 1.7 | |
| 4.2 | 3.3 | 2.9 | 2.7 | 2.5 | 2.4 | 2.1 | 1.9 | 1.6 | |
| 4.1 | 3.2 | 2.9 | 2.6 | 2.5 | 2.3 | 2.0 | 1.8 | 1.5 | |
| 4.0 | 3.2 | 2.8 | 2.5 | 2.4 | 2.3 | 1.9 | 1.7 | 1.4 | |
| 3.9 | 3.1 | 2.7 | 2.5 | 2.3 | 2.2 | 1.8 | 1.6 | 1.3 | |
| ¥ | 3.8 | 3.0 | 2.6 | 2.4 | 2.2 | 2.1 | 1.8 | 1.5 | 1.0 |
ПРИЛОЖЕНИЕ Б
Распределение Стьюдента.
Значения t–критерия Стьюдента при 5%-ном уровне значимости
| Число степеней свободы | Значения t-критерия |
| 12.71 | |
| 4.303 | |
| 3.182 | |
| 2.776 | |
| 2.571 | |
| 2.447 | |
| 2.365 | |
| 2.306 | |
| 2.262 | |
| 2.228 | |
| 2.201 | |
| 2.179 | |
| 2.160 | |
| 2.145 | |
| 2.131 | |
| 2.120 | |
| 2.110 | |
| 2.101 | |
| 2.093 | |
| 2.086 | |
| 2.080 | |
| 2.074 | |
| 2.069 | |
| 2.064 | |
| 2.060 | |
| 2.056 | |
| 2.052 | |
| 2.048 | |
| 2.045 | |
| 2.042 | |
| ¥ | 1.960 |
Приложение В
G-распределение Кохрена
(значение G*100 в зависимости от числа степени свободы γ1, γ2) и a = 0.05
| γ2 γ1 | ¥ | |||||||||||||
Приложение Г
| 25,40 | 26,63 | 24,66 | 28,21 | 29,58 | 27,39 | 5,04 | 5,28 | 4,89 | |||||
| 59,76 | 59,54 | 57,72 | 66,37 | 66,13 | 64,11 | 11,85 | 11,81 | 11,45 | |||||
| 47,40 | 47,23 | 46,17 | 52,64 | 52,45 | 51,28 | 9,40 | 9,37 | 9,16 | |||||
| 82,07 | 78,17 | 81,11 | 91,15 | 86,82 | 90,09 | 16,28 | 15,50 | 16,09 |
| 2,52 | 2,64 | 2,45 | 2,29 | 2,40 | 2,23 | 29,16 | 31,62 | 33,66 | |||||
| 5,93 | 5,90 | 5,72 | 5,39 | 5,37 | 5,21 | 72,89 | 71,16 | 75,80 | |||||
| 4,70 | 4,68 | 4,58 | 4,28 | 4,26 | 4,17 | 59,22 | 59,73 | 57,64 | |||||
| 8,14 | 7,75 | 8,04 | 7,41 | 7,05 | 7,32 | 95,08 | 99,11 | 101,75 |
| 19,41 | 21,05 | 22,41 | 9,71 | 10,52 | 11,20 | 4,85 | 5,26 | 5,60 | |||||
| 48,53 | 47,37 | 50,47 | 24,26 | 23,69 | 25,23 | 12,13 | 11,84 | 12,62 | |||||
| 39,42 | 39,76 | 38,37 | 19,71 | 19,88 | 19,19 | 9,86 | 9,94 | 9,59 | |||||
| 63,30 | 65,98 | 67,74 | 31,65 | 32,99 | 33,87 | 15,83 | 16,49 | 16,93 | |||||
| 4,42 | 4,79 | 5,10 | 5,33 | 5,70 | 6,01 | 3,46 | 3,70 | 3,91 | |||||
| 11,04 | 10,78 | 11,48 | 11,95 | 11,69 | 12,39 | 7,77 | 7,60 | 8,05 | |||||
| 8,97 | 9,05 | 8,73 | 9,88 | 9,96 | 9,64 | 6,42 | 6,47 | 6,27 | |||||
| 14,40 | 15,01 | 15,41 | 15,31 | 15,92 | 16,32 | 9,95 | 10,35 | 10,61 |
| 14,99 | 15,86 | 14,51 | 8,82 | 9,33 | 8,54 | 8,2 | 8,7 | 7,9 | |||||
| 34,98 | 34,13 | 33,61 | 20,58 | 20,08 | 19,77 | 19,9 | 19,4 | 19,1 | |||||
| 26,02 | 26,13 | 26,11 | 15,31 | 15,37 | 15,36 | 14,7 | 14,7 | 14,7 | |||||
| 46,21 | 46,42 | 48,43 | 27,18 | 27,31 | 28,49 | 26,5 | 26,7 | 27,8 | |||||
| 7,4 | 7,9 | 7,2 | 4,83 | 5,13 | 4,66 | 2,85 | 3,01 | 2,75 | |||||
| 18,1 | 17,7 | 17,4 | 11,79 | 11,49 | 11,31 | 6,64 | 6,48 | 6,38 | |||||
| 13,3 | 13,4 | 13,4 | 8,67 | 8,71 | 8,70 | 4,94 | 4,96 | 4,95 | |||||
| 24,1 | 24,3 | 25,3 | 15,69 | 15,77 | 16,47 | 8,77 | 8,81 | 9,19 |
| 7,05 | 7,64 | 8,14 | 27,94 | 29,58 | 30,94 | 11,51 | 13,15 | 14,51 | |||||
| 17,62 | 17,20 | 18,33 | 57,06 | 55,90 | 58,99 | 40,63 | 39,47 | 42,57 | |||||
| 14,32 | 14,44 | 13,94 | 47,95 | 48,29 | 46,90 | 31,52 | 31,86 | 30,48 | |||||
| 22,99 | 23,96 | 24,60 | 71,83 | 74,51 | 76,27 | 55,40 | 58,08 | 59,84 | |||||
| 16,50 | 17,30 | 16,02 | 21,61 | 23,15 | 20,69 | 2,19 | 2,30 | 2,13 | |||||
| 38,82 | 38,69 | 37,50 | 64,54 | 64,27 | 62,00 | 5,15 | 5,14 | 4,98 | |||||
| 30,80 | 30,69 | 30,00 | 49,10 | 48,88 | 47,57 | 4,09 | 4,07 | 3,98 | |||||
| 53,32 | 50,79 | 52,70 | 92,42 | 87,54 | 91,22 | 7,08 | 6,74 | 7,00 |
Заказ №______от «_____»___________ 2016______. Тираж__________экз.
СевГУ