Справочные материалы к заданию 3
Функцией распределения F(х) называется функция, равная вероятности того, что в результате опыта случайная величина Х примет значение, меньшее значения аргумента х: 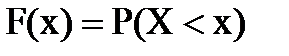 .
.
Условие нормировки:
для дискретной случайной величины 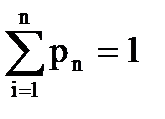 ;
;
для непрерывной случайной величины 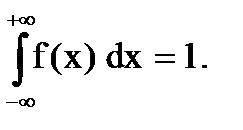
Соотношение между функцией распределения и плотностью распределения вероятностей для непрерывной случайной величины:
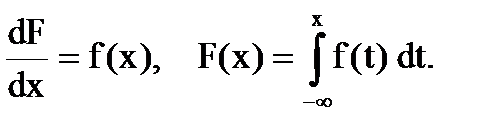
Вероятность попадания значения случайной величины в заданный интервал [a;b):
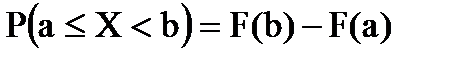 ;
;
для непрерывной случайной величины 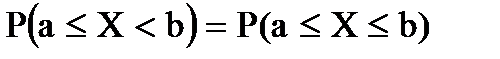 .
.
Математическое ожидание и дисперсия дискретной случайной величины вычисляются по формулам:
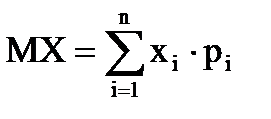 ,
, 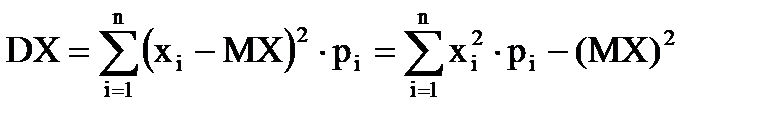 .
.
Математическое ожидание и дисперсия непрерывной случайной величины вычисляются по формулам:
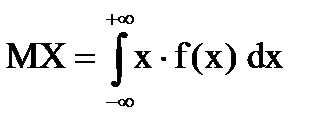 ,
,
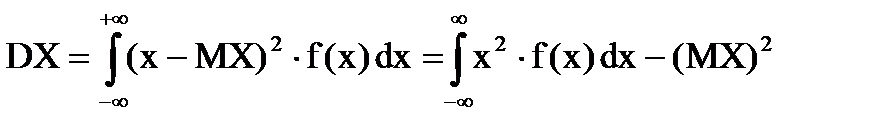 .
.
Задание 3.
Каждый вариант третьего задания состоит из двух пунктов:
3.1. Изучение закона распределения непрерывной величины;
3.2. Изучение закона распределения дискретной величины.
Задание 3.1.
Дана функция плотности распределения f(x) случайной величины Х.
1. Найдите значение константы с.
2. Постройте график функции плотности распределения y=f(x).
3. Найдите функцию распределения F(x) и постройте ее график.
4. Найдите математическое ожидание и дисперсию.
5. Найдите вероятность того, что значение случайной величины попадет в отрезок 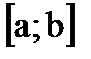 .
.
| N | 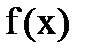 | a | b |
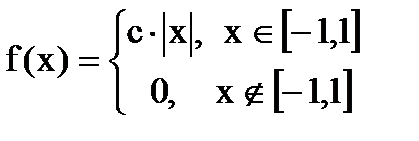 | 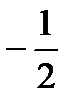 | 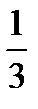 | |
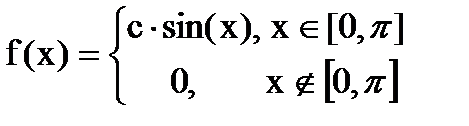 | 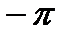 | 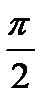 | |
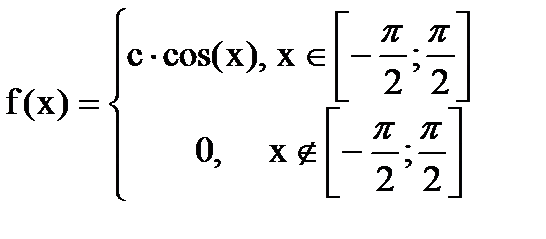 | 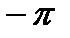 | ||
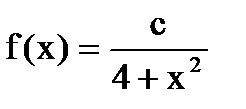 | 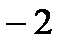 | ||
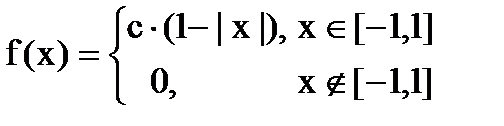 | 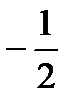 | 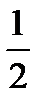 | |
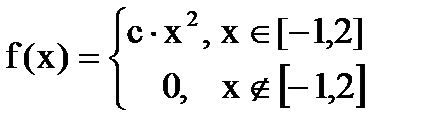 | |||
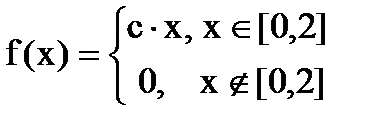 | 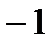 | ||
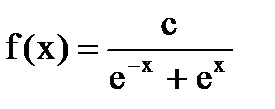 | |||
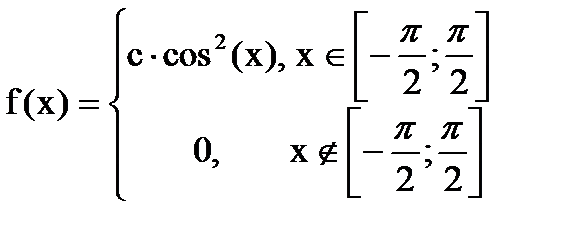 | 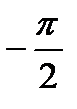 | 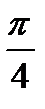 | |
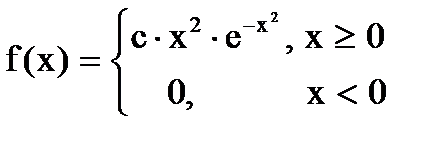 |  | ||
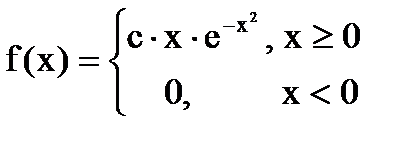 |  | ||
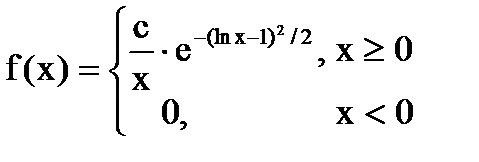 | |||
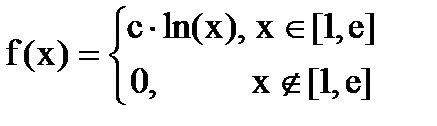 | 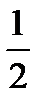 | 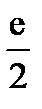 | |
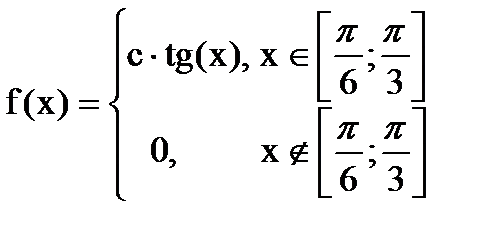 | 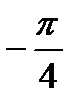 | 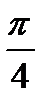 | |
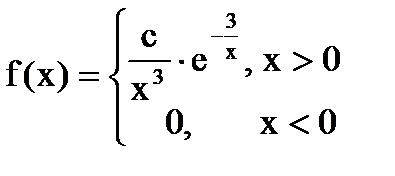 | |||
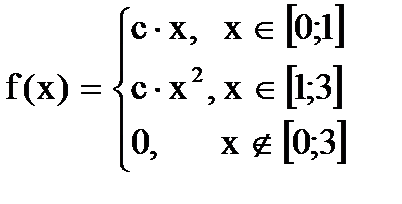 | |||
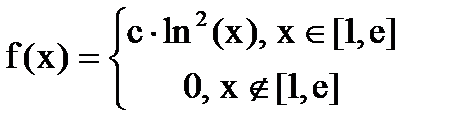 | 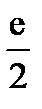 | ||
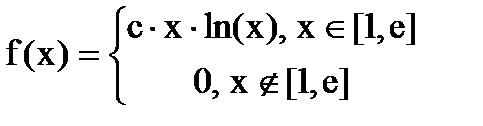 | 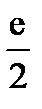 | ||
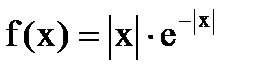 |  | ||
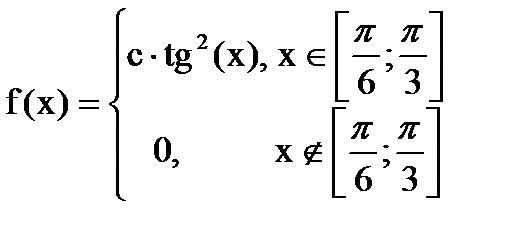 | 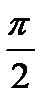 | 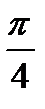 | |
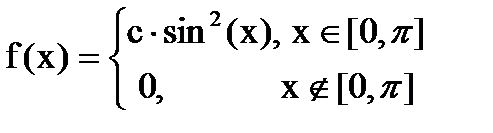 | 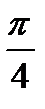 | 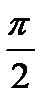 | |
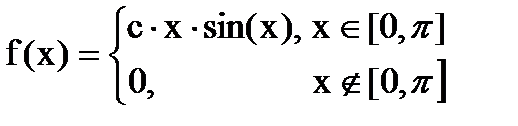 | 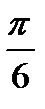 | 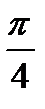 | |
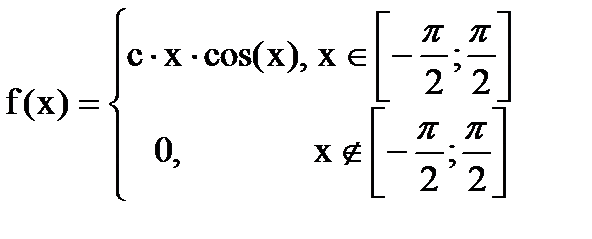 | 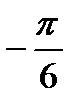 | 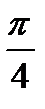 | |
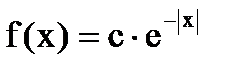 | 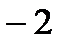 | ||
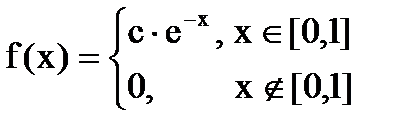 | 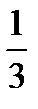 | 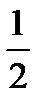 | |
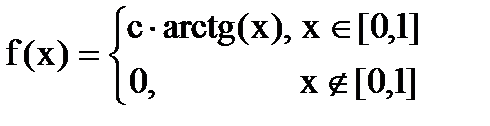 | 0.1 | 0.5 |
Пример выполнения задания 3.1. Вариант 26.
Используя условие нормировки, найдем значение константы:

Зададим плотность распределения (для определения кусочно-непрерывной функции используется AddLine панели математических инструментов programming) и построим ее график:


Вычисляя интеграл от плотности распределения, зададим функцию распределения вероятностей и построим ее график. В связи с тем, что, по умолчанию, вычисления в системе Mathcad проводятся с точностью до 20 знаков, воспользуемся функцией float панели Symbolic, которая позволяет выводить результат с выбранным количеством знаков, в данном примере с четырьмя.



Найдем математическое ожидание и дисперсию:


Найдем вероятность попадания случайной величины в отрезок 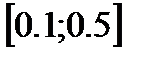 :
:
 .
.
Задание 3.2
Задан ряд распределения дискретной случайной величины.
1. Найдите значение р.
2. Постройте многоугольник распределения.
3. Вычислите математическое ожидание и дисперсию.
4. Найдите функцию распределения и постройте ее график.
5. Найдите вероятность того, что значение случайной величины попадет в интервал [a;b).
| Вариант 1 | Вариант 2 | Вариант 3 | |||
| x | p | x | p | x | p |
| 0.1 | -3 | 0.1 | -10 | 0.6 | |
| 0.01 | -2 | 0.1 | -3 | 0.05 | |
| 0.3 | 0.05 | 0.05 | |||
| 5,1 | p | 1.5 | 0.05 | p | |
| 5,2 | 0.3 | 1.7 | 0.07 | 0.1 | |
| 5,5 | 0.2 | p | 0.05 | ||
| a=2 b=4 | a=-1 b=1,8 | a=2 b=9 |
| Вариант 4 | Вариант 5 | Вариант 6 | |||
| x | p | x | p | x | p |
| 0,1 | -10 | 0,1 | 0,6 | ||
| 0,01 | -7 | 0,1 | 0,05 | ||
| 0,3 | -6.5 | 0,05 | 0,05 | ||
| 0.5 | p | -6 | 0,05 | p | |
| 0,3 | -4 | 0,07 | 0,1 | ||
| -1 | 0,2 | -1 | p | 0,05 | |
| a=1.5 b=2,5 | a=-9 b=-5 | a=2 b=12 |
| Вариант 7 | Вариант 8 | Вариант 9 | |||
| x | p | x | p | x | p |
| -2,5 | 0,05 | -8 | 2р | -3 | 0,2 |
| -2,2 | 0,15 | -3,5 | 0,2 | -1 | р |
| -2 | р | -1 | 0,15 | 0,05 | |
| -1,5 | 0,5 | -0,8 | 0,3 | 3,5 | 0,25 |
| -1,3 | 0,1 | -0,4 | р | 0,3 | |
| -0,8 | 0,05 | 0,2 | 0,05 | ||
| a=-1 b=1 | a=-6 b=-1,2 | a=-4 b=0 |
| Вариант 10 | Вариант 11 | Вариант 12 | |||
| x | p | x | p | x | p |
| 0,4 | 1,4 | 0,05 | 0,2 | ||
| 0,05 | 2,5 | 0,3 | р | ||
| 0,1 | 3,0 | р | 28,5 | 0,2 | |
| 0,15 | 6,5 | 0,2 | 2р | ||
| р | 7,9 | 0,15 | 0,15 | ||
| 0,2 | 0,2 | 0,05 | |||
| a=4 b=7 | a=2.8 b=7.5 | a=26 b=38 |
| Вариант 13 | Вариант 14 | Вариант 15 | |||
| x | p | x | p | x | p |
| -4,5 | 0,25 | -31 | 3р | -2 | 0,35 |
| -2 | 0,1 | -29 | 0,1 | -1,5 | 0,1 |
| -1,5 | р | -28 | 0,2 | -0,7 | р |
| -1 | 0,2 | -24 | 2р | 0,15 | |
| 0,05 | -21 | 0,4 | 0,25 | ||
| 0,25 | -19 | р | 0,1 | ||
| a=2 b=4 | a=-20 b=1 | a=2,4 b=9 |
| Вариант 16 | Вариант 17 | Вариант 18 | |||
| x | p | x | p | x | p |
| -4 | 0,2 | -13 | 0,05 | -6 | 0,1 |
| 0,1 | -10 | 0,1 | -2,5 | 0,15 | |
| 0,15 | -9 | 0,35 | -1 | р | |
| 0,05 | -6 | 0,25 | 0,2 | ||
| 0,3 | -5 | р | 0,05 | ||
| р | -2 | 0,1 | 0,2 | ||
| a=2 b=6 | a=-8 b=-4 | a=1 b=9 |
| Вариант 19 | Вариант 20 | Вариант 21 | |||
| x | p | x | p | x | p |
| 0,3 | -8,5 | 0,15 | р | ||
| р | -8 | 0,2 | 0,15 | ||
| 0,15 | -6 | 0,3 | 2,4 | 0,1 | |
| р | -3,5 | р | 3,5 | 0,25 | |
| 0,05 | -2,9 | 0,25 | 0,2 | ||
| 0,1 | -1 | р | 0,1 | ||
| a=32 b=38 | a=-7 b=-1.5 | a=2.2 b=8.5 |
| Вариант 22 | Вариант 23 | Вариант 24 | |||
| x | p | x | p | x | p |
| -6,5 | 0,4 | -8 | 0,25 | 1,2 | 0,05 |
| -4 | р | -7,2 | 0,3 | 1,5 | 3р |
| -2,7 | 0,15 | -6 | р | 1,9 | 0,2 |
| 0,1 | -1,8 | 2р | 2,3 | 2р | |
| 0,2 | 0,05 | 2,4 | 0,15 | ||
| 8,1 | 0,05 | 7,4 | 0,1 | 2,7 | 0,1 |
| a=3 b=5 | a=-12 b=12 | a=1.3 b=2.6 |
| Вариант 25 | Вариант 26 | ||
| x | p | x | p |
| -2 | 0,2 | -4 | 3р |
| 0,05 | -3,5 | 0,1 | |
| 0,1 | -1 | 0,15 | |
| 0,2 | 0,3 | ||
| р | 0,2 | ||
| 0,15 | 2,5 | 2р | |
| a=0 b=6 | a=-3 b=1,5 |
Пример выполнения задания 3.2. Вариант 26
Используя условие нормировки для дискретной случайной величины, составим уравнение, решив которое найдем значение р:

Представим значения случайной величины и вероятности их получения в результате опыта в виде вектор - столбцов:

и построим многоугольник распределения:

Вычислим математическое ожидание и дисперсию:


Зададим аналитически функцию распределения. Для этого отметим, что справедливы следующие утверждения:
если 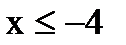 , то
, то 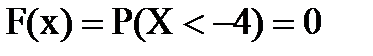 ;
;
если 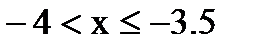 , то
, то 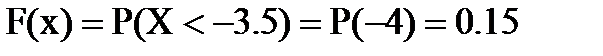 ;
;
если 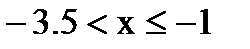 , то
, то 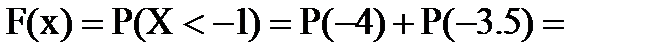
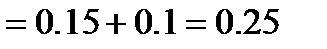 ;
;
если 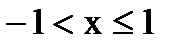 , то
, то 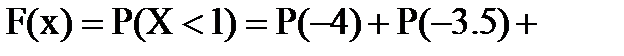
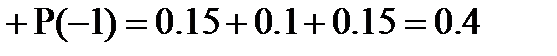 ;
;
если 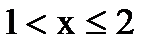 , то
, то 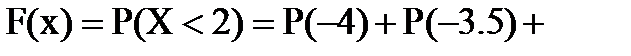
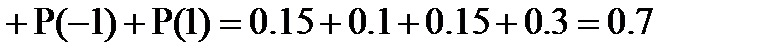 ;
;
если 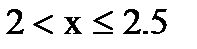 , то
, то 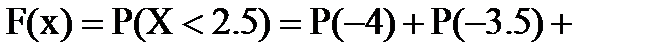
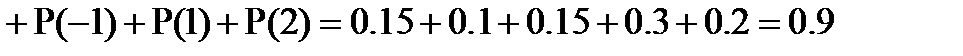 ;
;
если 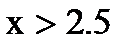 , то
, то 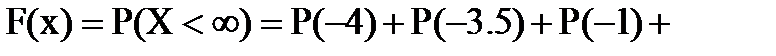
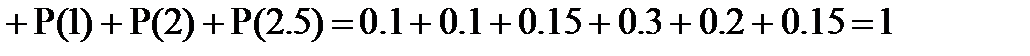
Как известно, функция распределения дискретной случайной величины является кусочно – постоянной, а ее график имеет ступенчатый вид. Вообще, график подобной функции в системе Mathcad содержит вертикальные линии, которые можно удалить, выполнив следующие действия: вызовите окно форматирования графика Formatting Currently Selected X-Y Plot, выберите закладку Traces,а в поле Type – тип построения линии points.
Чтобы задать в системе Mathcad кусочную функцию, введите имя функции и знак присваивания. Затем выберите панель Programming и на ней функцию Add Line. Введите выражение для вычисления функции F(y) на первом промежутке (замена аргумента х на у связана с особенностями выполнения задания в системе Mathcad). На той же панели Programming выберите функцию if и введите в свободной позиции неравенства, описывающие первый интервал. После этого перейдите в свободную позицию второй строки и повторите описанные выше действия. Для получения третьей строки необходимо выделить вторую строку, нажимая клавишу пробел, и выбрать функцию Add Line. Эти действия выполняются до получения всех 7 строк.

Построим график функции распределения F(y):

Найдем вероятность попадания значений случайной величины в интервал [-3;1.5):
 .
.
