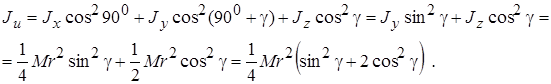Основные определения и характеристики

Материальной системой будем называть совокупность материальных точек, связанных между собой определенным образом (стержнями, нитями, винтами, пружинами и т.п. в том числе и силами взаимодействия).

Абсолютно твердое тело также является материальной системой, у которой точек бесконечное множество и связаны они между собой так, что расстояния между ними не изменяются, все время остаются постоянными.

Центром масс материальной системы называется геометрическая точка С, положение которой определяется радиусом-вектором 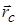таким, что

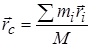, (14.1)

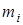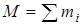где – радиусы-векторы отдельных точек с массами ; – масса всей системы.

Координаты центра масс:

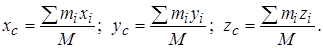(14.2)

Умножив числитель и знаменатель в (14.1) и (14.2) на g (ускорение свободного падения) убедимся, что вблизи поверхности Земли (g=const) центр масс совпадает с центром тяжести материальной системы, так как 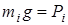– вес точек системы, сила тяжести их.

При исследовании движения материальной системы силы, действующие на ее точки, иногда приходится делить на классы. Или на внешние и внутренние или, теже силы, на активные (задаваемые) и реакции связей.

Внешними силами (обозначать будем 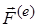) являются силы, действующие на точки системы со стороны точек, принадлежащих другим системам.

Внутренние силы ( 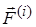) – силы взаимодействия между точками системы. Эти силы попарно равны по величине и направлены по одной прямой в противоположные стороны. Поэтому их главный вектор и главный момент относительно любой точки равны нулю: 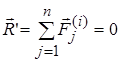и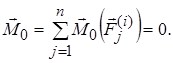

Конечно, при этом внутренние силы не всегда уравновешиваются: под действием этих сил отдельные точки системы могут перемещаться относительно друг друга.

Реакции связей или просто – реакции, это силы которые ограничивают движение точек системы (их координаты, скорость и др.). В статике это были силы заменяющие связи. В динамике для них вводится более общее определение.

Активными или задаваемыми силами называются все остальные силы, все кроме реакций.

Необходимость этой классификации сил выяснится в следующих главах.

Моменты инерции тел

Инерционные свойства твердого тела характеризуются не только его массой М, определяющей инерционность при поступательном движении, но и моментом инерции, определяющим инерционность вращательного движения тела.

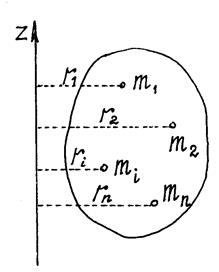Моментом инерции тела относительно оси называется сумма произведений массы каждой точки на квадрат расстояния от точки до оси (рис. 14.1).

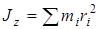. (14.3)

Заметим сразу, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.

Рис. 14.1.

Для однородных тел простой симметричной формы момент инерции можно найти в справочниках. А моменты инерции некоторых тел, которые чаще всего встречаются при исследовании движения материальных систем, даны в таблице 14.1.

Таблица 14.1

В таблице даны моменты инерции тел относительно осей симметрии. Но нередко при исследовании движения реальных механизмов приходится определять моменты инерции относительно осей, не совпадающих с осями симметрии. Этому помогают следующие теоремы.

Теорема Гюйгенса-Штейнера о моментах инерции тела относительно параллельных осей.

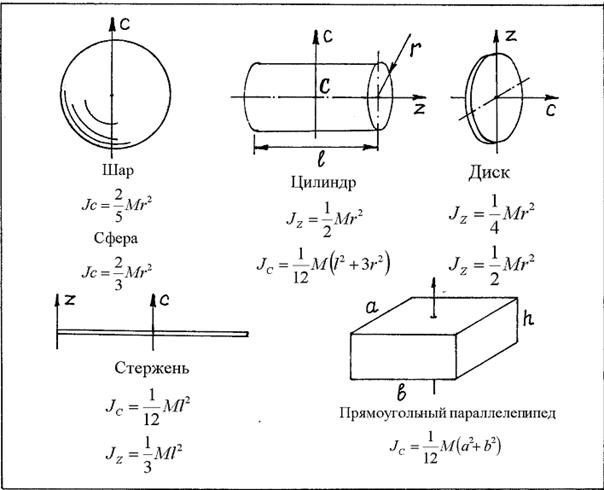
Найдем зависимость между моментами инерции тела относительно параллельных осей z и С (рис. 14.2). Ось С, приходящая через центр масс тела называется центральной осью. Расстояние между осями – а.

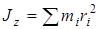По определению (14.3) . Но из заштрихованного прямоугольного треугольника (рис. 14.2) следует, что

.

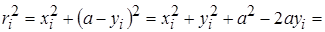
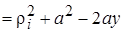Поэтому

Рис. 14.2.

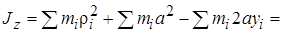
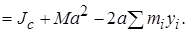
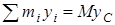Но, по (14.2), сумма и равна нулю, т.к. начало оси y выбрано в центре масс С (y_c=0).

Следовательно, момент инерции тела относительно оси z равен сумме момента инерции тела относительно центральной оси С, параллельной оси z, и произведения массы тела на квадрат расстояния между осями

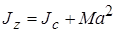. (14.4)

Так, например, момент инерции стержня относительно оси z (табл. 14.1) 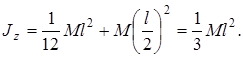А момент инерции прямоугольного параллелепипеда относительно оси z, проведенной по какому-нибудь вертикальному ребру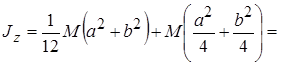

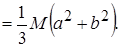
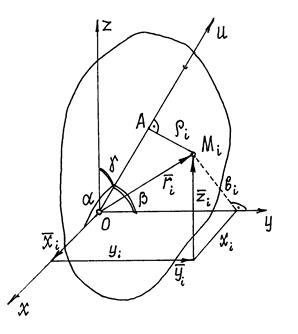
Момент инерции тела относительно произвольной оси.

Найдем момент инерции тела относительно оси u, проходящей через некоторую точку О (рис. 14.3).

Рис. 14.3.

По определению момент инерции .

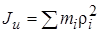Поместим в точку О начало координатных осей x, y, z. Из прямоугольного треугольника ОАМ_i следует 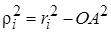, где 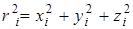. И так как радиус-вектор точки 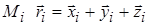, то, проектируя это равенство на ось u, получим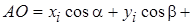 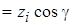(a, b, g - углы между осью u и осями x, y, z).

Рис. 14.3.

Как известно из тригономет­рии

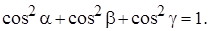
Поэтому 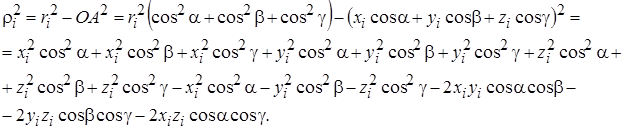И, группируя подобные члены, содержащие косинусы одинаковых углов, получим:

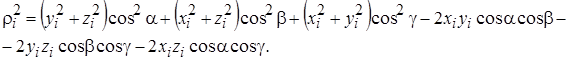
Но 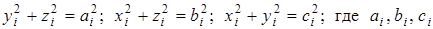- расстояния от точки М_i до осей x, y, z, соответственно. Поэтому

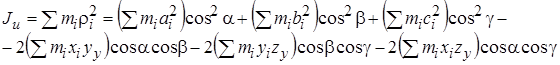
или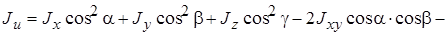

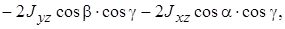(14.5)

где J_x, J_y, J_z – моменты инерции тела относительно осей координат; J_xy, J_yz, J_xz - центробежные моменты инерции относительно осей отмеченных в индексах.

Если два центробежных момента инерции, оба содержащих в индексах названия какой-нибудь одной оси, равны нулю, то эта ось называется главной осью инерции. Например, если J_yz = 0 и J_xz = 0, то ось z – главная ось инерции.

Так как все моменты инерции зависят от того, где находится точка О, от выбора начала координат, то обязательно надо указать для какой точки определены эти моменты инерции. Если начало координат взято в центре масс С, то все главные оси инерции называются главными центральными осями инерции.

Если в данной точке координатные оси являются главными осями инерции (центробежные моменты инерции относительно их равны нулю), то формула (14.5) упрощается:

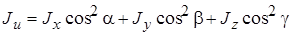. (14.6)

Иногда по некоторым признакам нетрудно найти главные оси инерции тела.

1. Если у однородного тела имеется ось симметрии, то эта ось является главной центральной осью инерции.

Действительно. Направим координатную ось z по оси симметрии. Тогда для каждой точки тела с координатами (x_i, y_i, z_i) можно отыскать точку с координатами (-x_i, -y_i, -z_i) и поэтому центробежные моменты инерци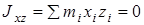и и 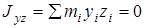. Значит ось z – главная ось инерции, и центральная ось, т.к. центр масс, как известно, находится на оси симметрии. Причём, эта ось будет главной для любой точки расположенной на оси симметрии.

2. Если у однородного тела имеется плоскость симметрии, то любая ось перпендикулярная ей будет главной осью инерции для всех точек этой плоскости.

Направим ось z перпендикулярно плоскости симметрии из любой её точки О, назначив там начало координат. Тогда для каждой точки тела с координатами (x_i, y_i, z_i) можно найти симметричную ей точку с координатами (x_i, y_i, - z_i). Поэтому центробежные моменты инерции J_xz и J_yz будут равны нулю. Значит ось z – главная ось инерции.

Пример 14.1. Определим момент инерции диска относительно оси u, расположенной под углом g к оси симметрии диска z (рис. 14.4).

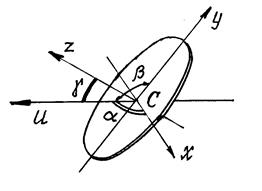
Оси x, y и z – главные центральные оси инерции, т.к. они являются осями симметрии.

Рис. 14.4.

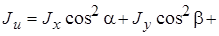
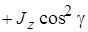Тогда , где g - угол между осями u и z; угол b - угол между осями u и y, равный (90⁰ +g); угол a - угол между осями u и x, равный 90°. Поэтому