Характерные особенности многошаговых процессов принятия решений. Принцип оптимальности Беллмана.
1. Природа задач, допускающая применение метода динамического программирования не меняется при изменении числа этапов, то есть их форма инвариантна относительно n.
2. Исходная задача погружается в класс однотипных задач, каждая из которых связана с отдельным этапом.
3. Каждому этапу сопоставляется оптимизационная задача, а процессу в целом совокупность оптимизационных задач.
4. Множество решений оптимизационных задач описывается системой функциональных уравнений, в этой системе каждое уравнение соответствует отдельному этапу и является рекуррентной.
5. Решение системы функциональных уравнений находится с помощью алгоритма прогонки: прямой или обратной.
6. Аналитической основой метода прогонки является принцип оптимальности.
Относительно характера управляемого процесса делаются следующие предположения:
1) Условия отсутствия последействия. Состояние, в котором окажется система в начале очередного этапа зависит от ее текущего состояния и выбранного управления и не зависит от того, каким образом система оказалась в текущем состоянии
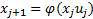
Будущее не зависит от прошлого, лишь от настоящее.
2) Условие аддитивности: предполагается, что функция F(x1,u),характеризующая управленческую стратегию u, представляется суммой отдельных функций, характеризующих этап.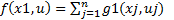 
При выполнении этих условия оптимальное решение на каждом этапе находится в силу принципа оптимальности Беллмана: оно должно быть таким, чтобы вклад текущего этапа + оптимальный вклад всех последующих были оптимальны.
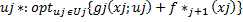
Оптимальный результат ф-ния системы на этапах j при условии, что в начале j+1 этапа система находилась в состоянии xj+1=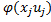 
С течением времени система должна перейти в финальное состояние xn+1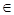 
Xn+1. Для оценки качества каждого управляемого решения u= 
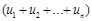оценивается функцией f(x1,u). u- вектор управления. Необходимо выбрать такую u*=(u1*, u2*,…un*) стратегию, которая доставляла бы оптимум показателя качества по совокупности всех возможных управленческих стратегий. f* = f*(x1,u*) = opt f(x1,u). Относительно характера управляемого процесса формулируем 2 принципа: 1.условие отсутствия последействия. Состояние, в котором окажется система на следующем этапе, зависит от ее текущего состояния и управления, принятого на данном этапе, но не зависит от способа, которым система оказалась в текущем состоянии.
2.свойство аддитивности. Качество управления uj, принятого на очередном этапе, оценивается функцией, зависящей от текущего состояния и выбранного управления: gj(xj, uj).Общая оценка всего процесса находится как сумма оценок по отдельным этапам:
.
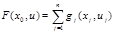Если процесс удовлетворяет условиям 1 и 2, то условно оптимальное решение на каждом этапе находится в силу принципа оптимальности Беллмана: каким бы ни было состояние системы перед очередным этапом, управление на данном этапе следует выбирать таким образом, чтобы результат данного этапа “+” оптимальный вклад всех последующих этапов в совокупности было оптимальным. fj(xj) = opt {gj(xj, uj) + f*j+1(xj+1)}; uj 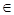U; xj+1 = φ(xj, uj).