II. Метод наименьших затрат
Найдем методом наименьших затрат первоначальное распределение поставок задачи №5.1. Выберем клетку с наименьшим коэффициентом затрат – клетку (2,3). Клетке (2,3) соответствует коэффициент затрат 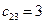 . В эту клетку дадим максимально возможную поставку:
. В эту клетку дадим максимально возможную поставку: 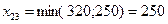 .
.
Мощности поставщика 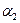 полностью реализованы, поэтому вычеркнем вторую строку.
полностью реализованы, поэтому вычеркнем вторую строку.
| поставщики | потребители | запасы | |||
 | 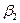 | 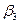 | 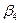 | ||
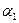 | |||||
 | |||||
 | |||||
| потребности |
Клетка (1,1), из оставшихся клеток, имеет наименьший коэффициент затрат - 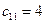 . Дадим в клетку (1,1) максимально возможную поставку
. Дадим в клетку (1,1) максимально возможную поставку 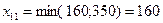 . В результате, чего потребности первого потребителя
. В результате, чего потребности первого потребителя 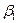 полностью удовлетворены. Вычеркнем из последующего рассмотрения первый столбец. Следующую поставку дадим в клетку (1,3):
полностью удовлетворены. Вычеркнем из последующего рассмотрения первый столбец. Следующую поставку дадим в клетку (1,3): 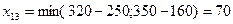 и вычеркнем третий столбец.
и вычеркнем третий столбец.
| поставщики | потребители | запасы | |||
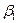 | 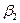 | 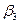 | 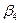 | ||
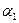 | |||||
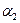 | |||||
 | |||||
| потребности |
Клетки (1,2) и (3,2) имеют равные коэффициенты затрат: 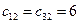 . Выберем для поставки третьего поставщика
. Выберем для поставки третьего поставщика 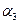 , так как за счет него можно полностью удовлетворить запросы второго потребителя. В клетку (3,2) дадим поставку
, так как за счет него можно полностью удовлетворить запросы второго потребителя. В клетку (3,2) дадим поставку 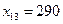 . Потребности потребителя
. Потребности потребителя 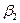 полностью удовлетворены.
полностью удовлетворены.
Дадим поставку в клетку (1,4): 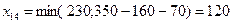 . На этом шаге выпадает из рассмотрения первая строка, мощности первого поставщика реализованы. Заполним последнюю клетку – клетку (3,4):
. На этом шаге выпадает из рассмотрения первая строка, мощности первого поставщика реализованы. Заполним последнюю клетку – клетку (3,4): 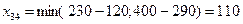 .
.
| поставщики | потребители | запасы | |||
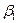 | 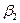 | 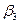 | 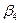 | ||
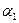 | |||||
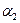 | |||||
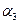 | |||||
| потребности |
Число заполненных клеток в данном распределении оказалось равным 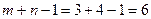 .
.
Общие суммарные затраты на перевозку всего груза методом наименьших затрат будут равны: 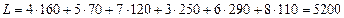 . Таким образом, первое опорное решение, построенное методом «наименьших затрат» дало лучший результат по сравнению с решением, построенным методом «северо-западного угла» (5200<5760). Но нельзя с уверенностью сказать, что полученное методом «наименьших затрат» решение будет оптимальным, то есть общая стоимость перевозок, равная 5200, будет наименьшей. Для проверки оптимальности полученного решения воспользуемся «методом потенциалов».
. Таким образом, первое опорное решение, построенное методом «наименьших затрат» дало лучший результат по сравнению с решением, построенным методом «северо-западного угла» (5200<5760). Но нельзя с уверенностью сказать, что полученное методом «наименьших затрат» решение будет оптимальным, то есть общая стоимость перевозок, равная 5200, будет наименьшей. Для проверки оптимальности полученного решения воспользуемся «методом потенциалов».
Метод потенциалов
Чтобы установить, является ли найденное опорное решение оптимальным, необходимо по определенному правилу каждому поставщику и каждому потребителю поставить в соответствие числа, которые должны удовлетворять определенным условиям. Назовем эти условия критерием оптимальности.
Критерий оптимальности: для того чтобы решение транспортной задачи было оптимальным, необходимо и достаточно, чтобы существовала система из 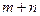 чисел
чисел 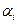 и
и 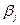 , которые удовлетворяли бы следующим условиям:
, которые удовлетворяли бы следующим условиям:
1) 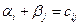 для занятых клеток; (5.6)
для занятых клеток; (5.6)
2) 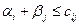 для свободных клеток. (5.7)
для свободных клеток. (5.7)
Числа 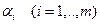 называются потенциалами пунктов отправления, числа
называются потенциалами пунктов отправления, числа 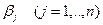 называются потенциалами пунктов назначения.
называются потенциалами пунктов назначения.
Замечание: пункты отправления (пункты назначения) и соответствующие им потенциалы обозначим одними и теми же буквами 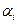 (
( 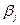 ), чтобы не вводить новые обозначения.
), чтобы не вводить новые обозначения.
Из критерия оптимальности следует, если хотя бы в одной из свободных клеток сумма соответствующих потенциалов превосходит коэффициент затрат, соответствующий этой клетке, то опорное решение является неоптимальным, и его можно улучшить.
Потенциалы 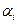 и
и 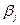 находим, решая систему уравнений (5.6).
находим, решая систему уравнений (5.6).
Эта система содержит 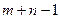 уравнений, ровно столько занятых клеток будет в опорном решении, а переменных
уравнений, ровно столько занятых клеток будет в опорном решении, а переменных 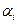 и
и 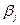 эта система содержит
эта система содержит 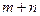 . Доказано, что система уравнений (5.6) является совместной неопределенной, ранг системы (5.6) равен
. Доказано, что система уравнений (5.6) является совместной неопределенной, ранг системы (5.6) равен 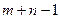 . Найдем любое решение системы (5.6), зафиксировав значение одной из переменных (обычно потенциалу
. Найдем любое решение системы (5.6), зафиксировав значение одной из переменных (обычно потенциалу 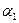 придают нулевое значение). После этого все остальные переменные определяются однозначно, причем решение имеет интересную особенность: зная значение одной переменной, сразу можно получить значение другой.
придают нулевое значение). После этого все остальные переменные определяются однозначно, причем решение имеет интересную особенность: зная значение одной переменной, сразу можно получить значение другой.
Вернемся к решению исходной транспортной задачи. Проверим опорное решение, полученное «методом наименьших затрат» на оптимальность.
Обнулим потенциал 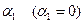 . По заданному
. По заданному 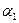 , легко найдем потенциалы
, легко найдем потенциалы 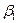 ,
, 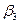 и
и 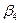 :
: 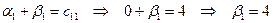 ;
;
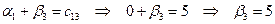 ;
;
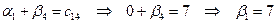 .
.
Значения потенциалов, по мере их нахождения, будем заносить в таблицу поставок.
| поставщики | потребители | запасы | |||
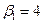 | 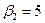 | 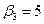 | 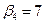 | ||
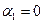 | 5 | 5 +   70 70 | 7 -  120 120 | ||
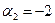 | 2 | 3 |  3 - 3 - | 4 + 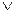 5 5 | |
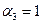 | 5 | 6 | |||
| потребности |
Зная, что 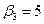 , найдем потенциал
, найдем потенциал 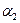 :
:
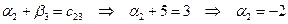 .
.
Зная, что 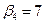 , а
, а 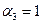 , найдем потенциалы
, найдем потенциалы 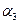 и
и 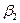 :
: 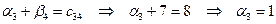 ;
;
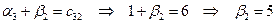 .
.
После того, как все потенциалы найдены, вычислим суммы соответствующих потенциалов для свободных клеток:
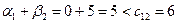 ;
;
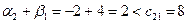 ;
;
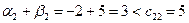 ;
;
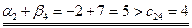 ;
;
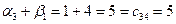 ;
;
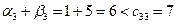 .
.
Полученные суммы потенциалов, запишем в левых нижних углах соответствующих свободных клеток. Чтобы не перепутать с поставками, суммы потенциалов в свободных клетках подчеркнем.
В клетке (2,4) сумма потенциалов больше соответствующего коэффициента затрат, следовательно, построенный опорный план не является оптимальным.
Для того чтобы улучшить план, составим цикл перераспределения поставок. Возьмем ту клетку, где сумма потенциалов больше коэффициента затрат. Если таких клеток несколько, то рациональнее выбрать ту клетку, в которой сумма потенциалов превосходит стоимость поставок на большую величину. В нашей задаче это будет клетка (2,4). Из этой клетки необходимо "прошагать шахматной ладьей" по занятым клеткам так, чтобы снова вернуться в исходную клетку, причем после каждого шага надо поворачивать "с горизонтали на вертикаль" или наоборот. Для каждой свободной клетки цикл по приведенному правилу составляется единственным образом.
Построим для клетки (2,4) цикл перераспределения поставок. В клетке (2,4) поставим знак "+" и из этой клетки перейдем либо в занятую клетку (2,3), либо в одну из занятых клеток (1,4) или (3.4), то есть в клетку, расположенную либо в той же строке, либо в том же столбце, что и клетка (2,4).
Если пойти в клетку (3,4), то из нее затем необходимо будет перейти в клетку (3.2), из которой в занятую клетку уже не попадешь, так как во втором столбце занятых клеток больше нет. Поэтому пойдем в клетку (2,3), поставим в ней знак "-". Из клетки (2,3) можно перейти только в занятую клетку (1,3). Перейдем в клетку (1,3), поставим в ней знак "+". Из этой клетки можно перейти либо в занятую клетку (1,1), либо в занятую клетку (1,4). Если пойти в клетку (1,1), то из нее затем в занятую клетку перейти нельзя, так как в первом столбце занятых клеток больше нет, поэтому из клетки (1,3) перейдем в клетку (1,4), поставим в ней знак "-" (после каждого шага знаки чередуются). Из клетки (1,4) вернемся в исходную клетку (2,4). Цикл замкнулся, обозначим его пунктирной линией.
Среди отрицательных вершин цикла (в клетках, где стоят знаки "-") выберем клетку с наименьшей по величине поставкой 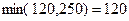 .
.
Перераспределим 120 единиц груза по построенному циклу. В тех клетках, где стоит знак "+" прибавим 120 единиц груза, в тех клетках, где стоит знак "-" вычтем этот груз. В результате этих операций общее количество груза ввозимое каждому потребителю и вывозимое от каждого поставщика, не изменится.
В новом опорном плане клетка (1,4) стала свободной, а клетка (2,4) занятой, то есть переменную 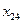 мы ввели в базис, а переменную
мы ввели в базис, а переменную 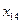 вывели из базиса. Число занятых клеток осталось прежним
вывели из базиса. Число занятых клеток осталось прежним 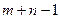 . Для полученного опорного решения, положив
. Для полученного опорного решения, положив 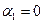 , снова найдем потенциалы из системы (5.6). Значения потенциалов по мере вычисления будем заносить в таблицу поставок. Затем вычислим суммы потенциалов для свободных клеток и проверим с помощью системы неравенств (5.7), является ли полученное решение оптимальным. В клетке (3.1) критерий оптимальности не выполнен:
, снова найдем потенциалы из системы (5.6). Значения потенциалов по мере вычисления будем заносить в таблицу поставок. Затем вычислим суммы потенциалов для свободных клеток и проверим с помощью системы неравенств (5.7), является ли полученное решение оптимальным. В клетке (3.1) критерий оптимальности не выполнен:
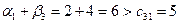 . Для клетки (3.1) построим замкнутый цикл перераспределения поставок. «Означим» цикл, начиная с клетки (3.1), присвоив ей знак «+», клетке (3.4) присвоим знак «-» и т. д.
. Для клетки (3.1) построим замкнутый цикл перераспределения поставок. «Означим» цикл, начиная с клетки (3.1), присвоив ей знак «+», клетке (3.4) присвоим знак «-» и т. д.
| поставщики | потребители | запасы | |||
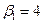 | 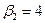 | 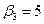 | 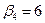 | ||
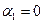 |   4 - 4 - | 4 |  5 + 5 + | 7 6 | |
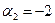 | 2 | 2 | 3 -  130 130 |  4 + 4 + | |
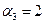 | 5 +   6 6 | 7 | 8 - | ||
| потребности |
Среди отрицательных вершин цикла выберем клетку с наименьшей по величине поставкой 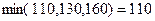 .
.
Перераспределим 110 единиц груза по построенному циклу. В тех клетках, где стоит знак "+" прибавим 110 единиц груза, в тех клетках, где стоит знак "-" вычтем этот груз.
| поставщики | потребители | запасы | |||
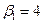 | 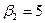 | 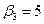 | 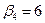 | ||
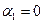 | 5 | 5 | 7 6 | ||
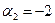 | 2 | 3 | |||
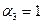 | 110 | 6 | 7 | ||
| потребности |
В новом опорном плане клетка (3,4) стала свободной, а клетка (3,1) занятой, то есть переменную 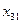 мы ввели в базис, а переменную
мы ввели в базис, а переменную 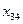 вывели из базиса. Проверим на оптимальность, полученное опорное решение: положив
вывели из базиса. Проверим на оптимальность, полученное опорное решение: положив 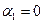 , вычислим значения остальных потенциалов. Как видно из последней таблицы поставок неравенство
, вычислим значения остальных потенциалов. Как видно из последней таблицы поставок неравенство 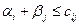 выполнено для всех свободных клеток. Следовательно, полученное опорное решение является оптимальным. Общая стоимость всех перевозок для данного плана будет наименьшей из всех возможных:
выполнено для всех свободных клеток. Следовательно, полученное опорное решение является оптимальным. Общая стоимость всех перевозок для данного плана будет наименьшей из всех возможных: 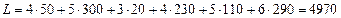 .
.
Ответ.Оптимальный план транспортировки груза:
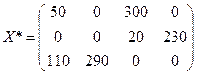 ,
,
при котором транспортные расходы по обеспечению продуктом всех четырех пуктов потребления будут равны 4970.
