Электрическое поле в вакууме. Электростатика

Электростатика

В статике напряженность электрического поля Е и магнитная индукция В не зависят от времени. Производные по времени от этих величин равны нулю. При этом уравнения Максвелла можно представить в виде двух независимых пар уравнений:

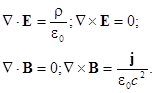
В статике электричество и магнетизм не связаны математически.

Электрическое поле в вакууме

Кулон экспериментально установил, что между двумя покоящимися зарядами действует сила, прямо пропорциональная произведению зарядов и обратно пропорциональна квадрату расстояния между ними. Сила направлена по прямой от одного заряда к другому.

Закон Кулона:

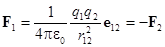
F₁ - сила, действующая на заряд q₁;

F₂ - сила, действующая на заряд q₂;

r₁₂ - расстояние между q₁ и q₂;

е₁₂ - единичный вектор, направленный от q₂ к q₁.

Множитель пропорциональности по историческим причинам пишется в виде 1/4pe₀. В системе единиц СИ, которой мы пользуемся, он определяется как 10^-7 от квадрата скорости света. Так как скорость света примерно 3×10⁸ м/сек, то множитель приблизительно равен 9×10⁹ ньютон×м²/кулон² , или вольт×м/кулон.

Принцип суперпозиции (следует из опыта):

сила, действующая на заряд, есть векторная сумма кулоновских сил, действующих со стороны всех прочих зарядов.

Если добавить к закону Кулона принцип суперпозиции, то это все, что есть в электростатике, больше ничего в ней не останется. Точно к таким же выводам, ни больше, ни меньше, приведут уравнения электростатики, приведенные в начале раздела.

Применяя закон Кулона, удобно ввести понятие об электрическом поле. Мы говорим, что поле в точке 1(c координатами x₁,y₁,z₁) Е(1) - это сила, действующая со стороны прочих зарядов на единицу заряда q₁. Кроме того, мы считаем, что Е(1) описывает нечто, существующее в точке (1), даже если в ней нет заряда q₁ (в предположении, что все прочие заряды сохранили свои позиции). Мы говорим: Е(1) - это электрическое поле в точке (1).

Если заряд q₂ расположен в точке (2) с координатами (x₂,y₂,z₂), то электрическое поле, создаваемое зарядом q₂, в точке (1) с координатами (x₁,y₁,z₁):

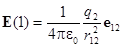
е₁₂ - единичный вектор, направленный от (2) к (1).

Это векторное уравнение, которое эквивалентно трем скалярным для проекций Е. Например, проекция поля на ось x равна:

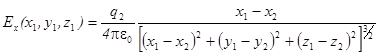
Если зарядов много, то поле Е в любой точке (1) равно векторной сумме вкладов от всех зарядов. По принципу суперпозиции:

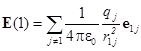
Если заряды размазаны по пространству с плотностью r(x,y,z):

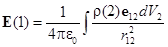(интегрирование ведется по всему объему, содержащему заряды)

r(2) - плотность заряда в (2);

dV₂ - объем, окружающий (2).

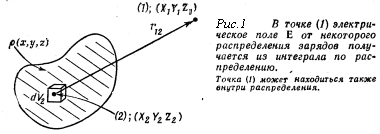
В задачах, используя симметрию в распределении зарядов, как правило, можно свести интегрирование по объему к интегрированию по одной переменной.

Работа по перемещению заряда в электростатическом поле.

Электростатический потенциал

Работа W, произведенная против действия электрической силы F(x,y,z,) при переносе заряда по некоторому пути L из точки (а) в точку (b):

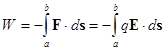(интегрирование ведется по пути L).

Вообще говоря, то, что получается при интегрированиях такого сорта, зависит от выбранного пути интегрирования. Но если бы интеграл зависел от пути, мы бы могли извлечь из поля работу, поднеся заряд к b по одному пути и унеся обратно к а по другому. Можно было бы подойти к b по тому пути, где W меньше, а удалиться по тому пути, где оно больше, получив работы больше, чем было вложено.

В принципе нет ничего невозможного в том, чтобы получать работу из поля. Такую же работу, согласно закону сохранения энергии, должны выполнить в данном случае заряды, которые являются источниками электростатического поля. Однако, в электростатике эти заряды неподвижны (основное допущение электростатики - положение зарядов не зависит от времени). Неподвижные заряды не могут совершить работу (работа, по определению, это произведение силы на путь). Следовательно, невозможно извлечь работу при перемещении заряда по замкнутому пути в электростатическом поле. А это значит, что работа по перемещению заряда в электростатическом поле не зависит от пути.

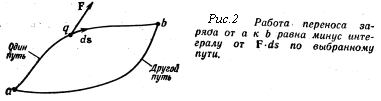
Удобно рассматривать работу переноса единицы заряда. Тогда сила, действующая на такой заряд, численно совпадает с электрическим полем. Обозначая в этом случае работу против действия электрических сил буквой W_един, напишем:

W_един (а ® b) =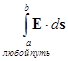

А раз выполняемая работа зависит только от концов пути, то она может быть представлена в виде разности двух чисел. В этом можно убедиться следующим образом. Выберем отправную точку Р₀ и договоримся рассчитывать интеграл, пользуясь только теми траекториями, которые проходят через точку Р₀. Обозначим работу, выполненную при движении против поля от Р₀ до точки а, через j(а), а работу на участке от Р₀ до точки b - через j(b) (рисунок). Работа перехода от а к Р₀ (по дороге к b) равна j(а) с минусом, так что

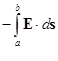= j(b) - j(а).

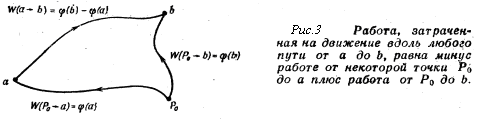
Так как повсюду будет встречаться только разность значений функции j в двух точках, то положение точки Р₀ в сущности безразлично. Однако как только отправная точка выбрана, число j тем самым определяется в любой точке пространства; значит, j является скалярным полем, функцией от х, у, z. Эту скалярную функцию мы называем электростатическим потенциалом в произвольной точке.

Пусть имеется отправная точка Р₀. Электростатическим потенциалом в произвольной точке Р называют скалярную функцию j(Р), равную работе по перемещению единичного положительного заряда по произвольному пути от отправной точки Р₀ к точке Р:

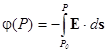, где интегрирование ведется по произвольному пути.

Часто удобно Р₀ брать на ¥. Тогда потенциал одиночного заряда q, расположенного в начале координат, в произвольной точке (x,y,z,) составляет:

.

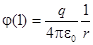По принципу суперпозиции потенциал поля, создаваемого совокупностью точечных зарядов равен алгебраической сумме потенциалов, создаваемых каждым из них:

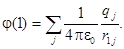
В случае непрерывного распределения зарядов в пространстве с объемной плотностью r(2) потенциал поля в точке (1) определяется интегралом по объему, содержащему заряды:

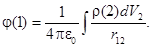Переменными интегрирования являются координаты точки (2). Координаты точки (1) являются в данном выражении константами. Эти координаты входят в выражение для модуля вектора перемещения от точки (2) к точке (1):

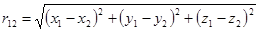
Физический смысл потенциала - потенциальная энергия, которую имел бы единичный положительный заряд при перемещении в данную точку пространства из некой отправной точки.

Связь напряженности поля и потенциала

С какой стати нас заинтересовал потенциал j? Силы, действующие на заряды, даются величиной Е - электрическим полем. Вся соль в том, что Е из j очень легко получить, не труднее, чем вычислить производную. Рассмотрим две точки с одинаковыми у, z, но с разными х: у одной х, у другой х + Dх; поинтересуемся, какую работу надо совершить, чтобы перенести единичный заряд из одной точки в другую. Путь переноса - горизонтальная линия от х до х + Dх. работа равна разности потенциалов в двух точках

.

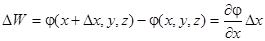Но работа против действия силы на том же отрезке равна

.

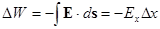Мы видим, что

.

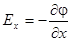Равным образом, 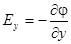, 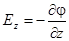; все это в обозначениях векторного анализа можно подытожить так:

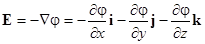
Отсюда следует, что 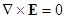(второе из уравнений Максвелла для электростатики). Ротор градиента всегда равен нулю (векторное произведение параллельных векторов). Электрическое поле электростатики - это поле без роторов.

Согласно, полученному выше уравнению

,

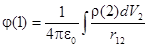скалярный потенциал j представляется трехмерным интегралом, подобным тому, который мы писали для Е:

.

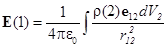Есть ли какая-то выгода в том, что вместо Е вычисляется j? Да. Для вычисления j нужно взять один интеграл, а для вычисления Е - три (ведь это вектор, необходимо определить три его проекции). Кроме того, обычно 1/r интегрировать легче, чем х/r³. Во многих практических случаях оказывается, что для получения электрического поля легче сперва подсчитать j, а после взять градиент, чем вычислять три интеграла для Е. Это просто вопрос удобства. Но потенциал имеет также глубокий физический смысл и представляет самостоятельный интерес для практики.

Следует подчеркнуть важный факт. Для любой радиальной силы выполняемая работа не зависит от пути и существует потенциал. Если вдуматься в это, можно увидеть, что интеграл работы не зависит от пути в любом радиальном, сферически симметричном поле. То, что зависимость силы от расстояния имела вид 1/r², не имело никакого значения, при любой зависимости от r получилось бы то же самое. Существование потенциала и обращение в нуль ротора Е вытекает на самом деле только из симметрии и направленности электростатических сил.

Свойства потока вектора напряженности электрического поля

Теперь мы хотим вывести уравнение, которое непосредственно и в лоб учитывает тот факт, что закон силы - это закон обратных квадратов. Может показаться вполне естественным, что поле меняется обратно пропорционально квадрату расстояния, потому что «именно так, мол, все распространяется». Возьмем световой источник, из которого льется поток света; количество света, проходящее через основание конуса с вершиной в источнике, одно и то же независимо от того, насколько основание удалено от вершины. Это с необходимостью следует из сохранения световой энергии. Количество света на единицу площади - интенсивность - должно быть обратно пропорционально площади, вырезанной конусом, т.е. квадрату расстояния от источника. Ясно, что по той же причине и электрическое поле должно изменяться обратно квадрату расстояния!

Но здесь ведь нет ничего похожего на «ту же причину». Ведь никто не может сказать, что электрическое поле есть мера чего-то такого, что похоже на свет и что поэтому должно сохраняться. Если бы у нас была такая «модель» электрического поля, в которой вектор поля представлял бы направление и скорость (ну, например, был бы током) каких-то вылетающих маленьких «дробинок», и если бы эта модель требовала, чтобы число дробинок сохранялось и ни одна не могла пропасть после вылета из заряда, вот тогда мы могли бы говорить, что «чувствуем» неизбежность закона обратных квадратов. С другой стороны, непременно должен был бы существовать математический способ выражения этой физической идеи. Если бы электрическое поле было подобно сохраняющимся дробинкам, то оно менялось бы обратно пропорционально квадрату расстояния и мы могли бы описать такое поведение некоторым уравнением, т.е. чисто математическим путем. Если мы не утверждаем, что электрическое поле сделано из дробинок, а понимаем, что это просто модель, помогающая нам прийти к правильной математической теории, то ничего плохого в таком способе рассуждений нет.

Предположим, что мы на мгновение представили себе электрическое поле в виде потока чего-то сохраняющегося и текущего повсюду, за исключением того места, где расположен сам заряд (должен же этот поток откуда-то начинаться). Представим что-то (что именно неважно), вытекающее из заряда в окружающее пространство. Если бы Е было вектором такого потока, то вблизи от точечного источника оно обладало бы зависимостью 1/r². Теперь мы желаем использовать эту модель для того, чтобы глубже сформулировать закон обратных квадратов.

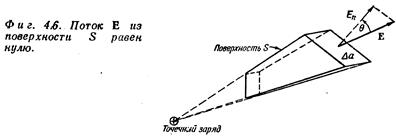
Спросим себя: чему равно «вытекание» Е из произвольной замкнутой поверхности в окрестности точечного заряда? Для начала возьмем простенькую поверхность - такую, как показано на рисунке.

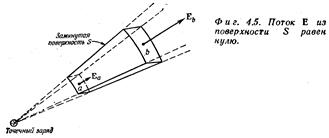
Если поле Е похоже на поток, то суммарное вытекание из этого ящика должно быть равно нулю. Это и получается, если под «вытеканием» из этой поверхности мы понимаем поверхностный интеграл от нормальной составляющей Е, т.е. поток Е в том смысле, как определено в математике. На боковых гранях нормальная составляющая Е равна нулю. На сферических гранях нормальная составляющая Е равна самой величине Е, с минусом на меньшей грани и с плюсом на большей. Величина Е убывает как 1/r², а площадь грани растет как r², так что их произведение от r не зависит. Приток Е через грань а в точности гасится оттоком через грань b. Суммарный поток через S равен нулю, а это все равно, что сказать:

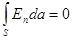на этой поверхности.

Теперь покажем, что две «торцевые» поверхности могут быть без ущерба для величины интеграла перекошены относительно радиуса. Хотя это верно всегда, но для наших целей достаточно только показать, что это справедливо тогда, когда «торцы» малы и стягивают малый угол. На рисунке показана поверхность S, «боковые грани» которой радиальны, а «торцы» перекошены. На рисунке они не малы, но надо представить себе, что на самом деле они очень малы. Тогда поле Е над поверхностью будет достаточно однородным, так что можно взять его значение в центре. Если торец наклонен на угол q, то его площадь возрастает в 1/соsq раз, а Е_n - компонента Е, нормальная к поверхности торца, убывает в соsq раз, так что произведение Е_nDa не меняется. Поток из всей поверхности S по-прежнему равен нулю.

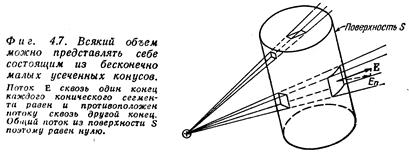
Теперь уже легко разглядеть, что и поток из объема, окруженного произвольной поверхностью S, обязан быть равным нулю. Ведь любой объем можно представить себе составленным из таких частей, как на последнем рисунке. Вся поверхность разделится на пары торцевых участков, а поскольку потоки через каждую из них внутрь и наружу объема попарно уничтожаются, то и суммарный поток через поверхность обратится в нуль. Идея эта иллюстрируется рисунком.

Мы получаем совершенно общий результат: суммарный поток Е через любую поверхность S в поле точечного заряда равен нулю.

А что случилось бы, если бы точечный заряд оказался внутри поверхности S. Это можно определить с помощью фокуса. Допустим, что мы «убрали» заряд «изнутри», окружив его маленькой поверхностью 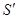так, чтобы она лежала целиком внутри первоначальной поверхности S (рисунок). Теперь в объеме, заключенном между двумя поверхностями S и 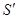, никакого заряда нет. Общий поток из этого объема (включая поток через 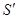) равен нулю, в чем можно убедиться при помощи прежних аргументов. Они говорят нам, что поток через 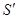внутрь объема такой же, как поток через S наружу. Для 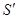мы можем выбрать любую, какую угодно форму, поэтому давайте сделаем ее сферой с зарядом в центре (рисунок). Тогда поток через нее подсчитать легко.

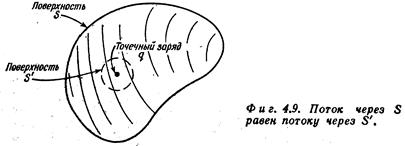
Для точечного заряда q поток Е через сферу радиуса r равен 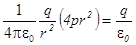, т.е. равен числу, не зависящему от радиуса сферы! Значит и поток наружу через S тоже равен q/e₀. Такой же поток выйдет из любой замкнутой поверхности, содержащей внутри точечный заряд q.

Пользуясь принципом суперпозиции, можно обобщить этот вывод на поле, формируемое любой совокупностью зарядов. Отсюда следует закон или теорема Гаусса:

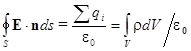, где замкнутая поверхность S ограничивает объем V, а заряд Q = 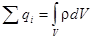- это суммарный заряд (совокупность точечных зарядов q_i, или размазанный по пространству заряд с объемной плотностью r), который сосредоточен в объеме V, ограниченном поверхностью S.

Закон Гаусса эквивалентен первому уравнению Максвелла, которое можно рассматривать как дифференциальную форму закона Гаусса, действительно:

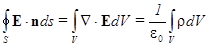(При преобразовании поверхностного интеграла в объемный мы воспользовались математической теоремой Остроградского-Гаусса. Напомним смысл этой теоремы. Важнейшее свойство потока любого вектора из замкнутой поверхности, в нашем случае 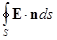, состоит в том, что этот поток равен сумме потоков из всех частей объема V, ограниченного данной поверхностью, или просто интегралу по объему V от объемной плотности потока. Теорема утверждает, что объемной плотностью потока является дивергенция вектора, в нашем случае 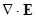. Таким образом, ).

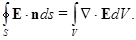Два объемных интеграла в последней формуле осуществляют суммирование по одному и тому же объему и их равенство означает равенство подинтегральных функций. Отсюда получаем первое уравнение Максвелла:

.

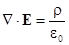Таким образом, первое уравнение Максвелла эквивалентно закону Кулона, пользуясь которым мы получили закон Гаусса, т.е. напрямую связано с законом обратных квадратов.

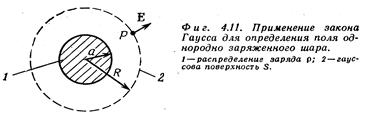
Наглядное представление конфигурации поля с помощью силовых линий

Поле можно для наглядности представить в виде совокупности силовых линий поля и эквипотенциальных поверхностей. В каждой точке пространства вектор напряженности поля направлен по касательной к силовой линии. Таким образом, силовые линии наглядно характеризуют направленность поля в пространстве. Густота расположения линий (количество линий, приходящихся на единицу площади, перпендикулярной линиям) пропорциональна модулю вектора напряженности поля. Получается, что поток вектора напряженности поля через какую-либо поверхность пропорционален количеству силовых линий, пересекающих эту поверхность.

Согласно закону Гаусса, поток напряженности поля через любую поверхность пропорционален суммарному заряду, находящемуся внутри этой поверхности. Т.е. источниками силовых линий являются положительные заряды, заканчиваются силовые линии на отрицательных зарядах, или на бесконечности. Количество силовых линий, исходящих из заданной совокупности зарядов и пересекающих окружающую эти заряды замкнутую поверхность, очевидно, не зависит от формы поверхности.

Поток через замкнутую поверхность, не содержащую внутри электрических зарядов, равен нулю. Силовые линии пересекают такую поверхность насквозь. Какое количество их входит в поверхность - такое и выходит. Т.е. входящий поток напряженности поля компенсируется выходящим потоком противоположного знака.

Применение закона Гаусса

Поле заряженного шара.

Когда мы изучали теорию гравитационного притяжения, то приняли без доказательства, что сила, создаваемая твердым шаром на его поверхности, такая же, как если бы все вещество шара было сконцентрировано в его центре. Много лет Ньютон не решался обнародовать свою теорию тяготения, так как не был уверен в правильности этой теоремы. Доказательство можно было бы осуществить путем мысленного разбиения шара на мелкие точечные массы и, затем, к векторному суммированию сил взаимодействия данного тела с каждой из точечных масс. Математически суммирование свелось бы к вычислению интеграла по объему шара, что математически сложно. Теперь эту теорему мы можем доказать очень просто. Но на этот раз мы докажем не совсем ее, а сходную теорему для однородно заряженного электричеством шара. (Поскольку законы электростатики и тяготения совпадают, то же доказательство может быть проведено и для поля тяготения.)

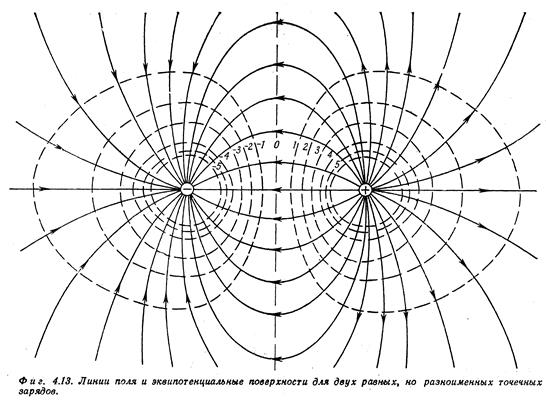
Зададим вопрос: каково электрическое поле Е а точке Р где-то снаружи сферы, наполненной однородно распределенным зарядом? Так как здесь нет «выделенного» направления, то законно допустить, что Е всюду направлено прямо от центра сферы. Рассмотрим воображаемую сферическую поверхность, концентрическую со сферой зарядов и проходящую через точку Р (рисунок). Все точки этой сферы в силу симметрии равноправны по отношению к заряду, поэтому считаем, что напряженность поля во всех этих точках одинакова по величине и направлена перпендикулярно поверхности сферы (нормальная к поверхности компонента напряженности равна модулю напряженности поля). Для этой сферы поток наружу равен

.

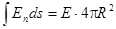Закон Гаусса утверждает, что этот поток равен суммарному заряду сферы Q (деленному на e₀):

,

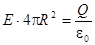или

,

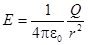а это как раз та формула, которая получилась бы для точечного заряда Q. Мы решили проблему Ньютона проще, без интеграла. Конечно, это кажущаяся простота; пришлось затратить какое-то время на то, чтобы разобраться в законе Гаусса. Но когда придется часто применять эту теорему, она окупается сторицей.

Равновесие в электростатическом поле

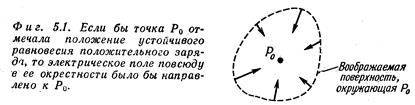
Можно доказать, что любая конфигурация зарядов в свободном состоянии не может находиться в состоянии устойчивого равновесия в электрическом поле. Применяя закон Гаусса, легко понять почему. Ограничимся отдельным точечным зарядом. Во-первых, чтобы заряд пребывал в равновесии в некоторой точке Р₀, поле в ней должно быть равно нулю. Во-вторых, чтобы равновесие было устойчивым, требуется, чтобы смешение заряда из Р₀ в любую сторону вызывало восстанавливающую силу, направленную против смещения. Векторы электрического поля во всех окрестных точках должны показывать внутрь - на точку Р₀. Но как легко видеть, это нарушает закон Гаусса, если в Р₀ нет заряда.

Возьмем небольшую воображаемую поверхность, окружающую точку Р₀ (рисунок). Если повсюду вблизи Р₀ электрическое поле направлено к Р₀, то поверхностный интеграл от нормальной составляющей определенно не равен нулю. В случае, изображенном на рисунке, поток через поверхность должен быть отрицательным числом. Но, согласно закону Гаусса, поток электрического поля сквозь любую поверхность пропорционален количеству заряда внутри нее. Если в Р₀ нет заряда, то изображенное нами поле нарушит закон Гаусса. Уравновесить положительный заряд в пустом пространстве, в точке, в которой нет какого-нибудь отрицательного заряда, невозможно. Но если положительный заряд размещен в центре распределенного отрицательного заряда, то он может находиться в равновесии. Конечно, распределение отрицательного заряда должно само удерживаться на своем месте посторонними, неэлектрическими силами.

Закон Гаусса может эффективно использоваться для нахождения полей, формируемых распределениями зарядов, которые отличаются сферической, цилиндрической и плоскостной симметрией.

Поле заряженной прямой линии

Пусть заряды равномерно распределены по длине бесконечно длинной прямой, так что на единицу длины приходится заряд l. Мы хотим определить электрическое поле. Конечно, задачу можно решить интегрированием вкладов в поле от всех частей прямой. Но мы собираемся решить ее без интегрирования, только с помощью закона Гаусса и некоторых догадок. Во-первых, легко догадаться, что электрическое поле будет направлено по радиусу. Любой осевой составляющей от зарядов, лежащих от одной стороны от некоторой плоскости, должна отвечать такая же осевая составляющая от зарядов, лежащих с другой стороны. В итоге должно остаться только радиальное поле. Кроме того, резонно полагать, что во всех точках, равно отстоящих от прямой, поле имеет одинаковую величину. Это очевидно. (Может быть, это нелегко доказать, но это верно, если пространство симметрично, а мы считаем что это так.)

Применить закон Гаусса можно следующим образом. Вообразим себе поверхность, имеющую форму цилиндра, ось которого совпадает с нашей прямой (рисунок). Согласно закону Гаусса, весь поток Е из этой поверхности равен заряду внутри нее, деленному на e₀. Раз поле считается нормальным к поверхности, то его нормальная составляющая - это величина вектора поля. Обозначим ее Е. Пусть радиус цилиндра будет r, а длина его для удобства выбрана равной единице. Поток сквозь цилиндрическую поверхность равен произведению Е на площадь поверхности, т.е. на 2pr. Поток через торцы равен нулю, потому что поле касательно к ним. Весь заряд внутри нашей поверхности равен как раз l, потому что длина оси цилиндра равна единице. Тогда закон Гаусса дает

.

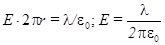Электрическое поле заряженной прямой обратно пропорционально первой степени расстояния от прямой.

Заряженная плоскость; пара плоскостей.

Рассчитаем поле однородно заряженного плоского листа. Предположим, что лист имеет бесконечную протяженность и заряд на единицу площади равен s. Сразу приходит в голову следующее соображение: из симметрии следует, что поле направлено всюду поперек плоскости, и если не существует поля от всех прочих зарядов в мире, то поля по обе стороны плоскости должны совпадать по величине. На этот раз за гауссову поверхность мы примем прямоугольный ящик, пересекающий нашу плоскость (рисунок). Каждая из граней, параллельных плоскости, имеет площадь S. Поле нормально к этим двум граням и параллельно остальным четырем. Суммарный поток равен Е, умноженному на площадь первой грани, плюс Е, умноженному на площадь противоположной грани; от остальных граней никаких слагаемых не войдет. Заряд внутри ящика равен sS. Уравнивая поток с зарядом, напишем

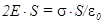
откуда

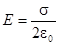
Простой, но важный результат.

Видим, что поле является однородным и не зависит от расстояния до плоского заряда.

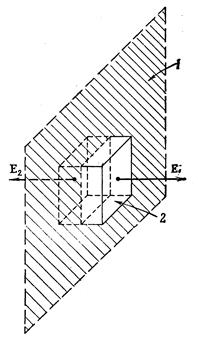
Задача о двух параллельных плоскостях с равными и противоположными плотностями зарядов +s и -s решается тоже просто, если только снова предположить, что внешний мир абсолютно симметричен. Составим ли мы суперпозицию двух решений для отдельных плоскостей или построим гауссов ящик, охватывающий обе плоскости, в обоих случаях легко видеть, что поле снаружи плоскостей равно нулю (рисунок). Но, заключив в ящик только одну или только другую поверхность, как показано на рисунке, мы легко обнаружим, что поле между плоскостями должно быть вдвое больше поля отдельной плоскости. Итог таков:

поле между пластинами Е = s/e₀, поле снаружи равно Е = 0

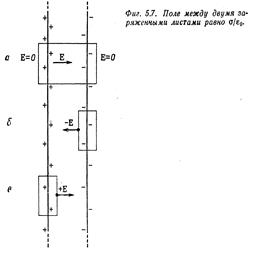
Однородно заряженный шар

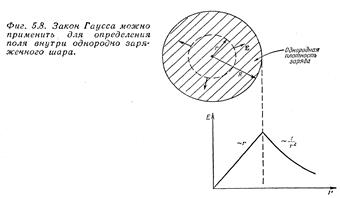
Для однородно заряженного шара, имеющего объемную плотность заряда r, при r<R (внутри шара), пользуясь приведенными выше соображениями симметрии, можем записать закон Гаусса для сферической гауссовой поверхности радиуса r:

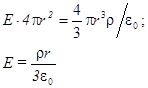
Видим, что внутри однородно заряженного шара поле пропорционально расстоянию r от центра и направлено по радиусу наружу.

Снаружи шара - как для точечного заряда:

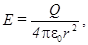где 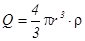(полный заряд шара).

Поле проводника

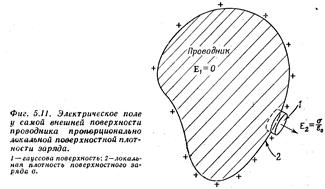
Проводник - твердое тело, в котором есть много «свободных» электронов. Электроны могут двигаться в веществе свободно, но не могут выйти за его пределы. За счет этого поле внутри проводника в условиях электростатики равно 0. Потенциал всюду в пределах проводника имеет постоянное значение. Можно доказать с помощью закона Гаусса, что плотность зарядов во всех внутренних частях проводника и в том числе на стенках полостей равна 0. Весь нескомпенсированный заряд локализуется в пределах тонкого слоя на поверхности проводника, где удерживается большими силами. Электрическое поле возле самой поверхности должно быть нормально к поверхности. Касательной составляющей быть не может.

Применяя закон Гаусса, мы можем связать напряженность поля у самой поверхности проводника с локальной плотностью заряда на поверхности. За гауссову поверхность мы примем небольшой цилиндрический стакан, наполовину выдвинутый из него (рисунок). Вклад в общий поток Е дает только та часть стакана, которая находится вне проводника. Тогда поле у наружной поверхности проводника Е = s/e₀, где s - локальная поверхностная плотность заряда.

Почему слой зарядов на проводнике создает не такое поле, как слой зарядов сам по себе, а вдвое больше? Но ведь мы не утверждали, будто в проводнике нет больше никаких других зарядов. В действительности для того, чтобы в проводнике Е было равно нулю, в нем обязательно должны присутствовать какие-то заряды. В непосредственной близости от точки Р на поверхности заряды действительно создают поле Е_лок = s_лок/2e₀ как внутри, так и снаружи поверхности. Но прочие заряды проводника сообща «устраивают заговор», чтобы создать в точке Р добавочное поле, равное по величине Е_лок. Суммарное внутреннее поле обращается в нуль, а наружное удваивается.

Поле внутри полости проводника

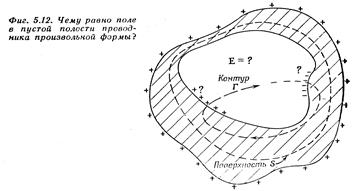
Рассмотрим проблему пустотелого резервуара - проводника, имеющего внутри полость. В металле поля нет, а вот есть ли оно в полости? Покажем, что если полость пуста, то поля в ней быть не может, какова бы ни была форма проводника или полости (рисунок). Рассмотрим гауссову поверхность, подобную S на рисунке, которая окружает собой полость, но остается всюду в веществе проводника. Всюду на поверхности S поле равно нулю, так что потока сквозь S быть не может, а суммарный заряд внутри S должен быть равен нулю. Затем можно вывести из симметрии, что на внутренней поверхности сферической оболочки нет никакого заряда. Но в более общем случае мы только можем сказать, что на внутренней поверхности проводника имеется равное количество положительного и отрицательного зарядов. Может быть, окажется, что на одной части имеется положительный заряд, а где-то в другом месте - отрицательный (рисунок)? такие вещи законом Гаусса не исключаются.

На самом деле, конечно, получается, что равные, но противоположные заряды на внутренней поверхности должны были бы соскользнуть навстречу друг другу и уничтожить друг друга. Мы можем убедиться в том, что они уничтожат друг друга, применив закон о равенстве нулю циркуляции Е (в электростатике). Пусть на каких-то частях внутренней поверхности оказались заряды. Мы знаем, что еще где-то должно присутствовать равное количество противоположных зарядов. Но любые линии поля Е начинаются на положительных зарядах и кончаются на отрицательных (мы рассматриваем случай, когда свободных зарядов в полости нет). Представим себе теперь контур Г, пересекающий полость вдоль линии силы от какого-то положительного заряда к какому-то отрицательному и возвращающийся к исходной точке по телу проводника (рисунок). Интеграл вдоль такой линии сил в пределах от положительного до отрицательного заряда не был бы равен нулю, а интеграл по пути через металл равен нулю, так как там Е = 0. Так что мы бы имели

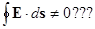
Но криволинейный интеграл от Е по любому замкнутому контуру в электростатическом поле всегда равен нулю. Значит, внутри пустой полости не может быть никаких полей, равно как не может быть никаких зарядов на внутренней поверхности.

Мы показали, что если полость целиком окружена проводником, то никакое статическое распределение зарядов снаружи никогда не создаст поля внутри. Это объясняет принцип «защиты» электрического оборудования, которое помещается в металлическую коробку. В электростатике (но не в изменяющихся полях) поля по обе стороны сплошной проводящей оболочки полностью не зависят одно от другого.

Электрический диполь

Пара одинаковых по величине, но разноименных по знаку зарядов q, расстояние d между которыми намного меньше расстояния до точек, в которых рассматривается их поле, называют диполем.

Диполи встречаются очень часто. Важнее всего, пожалуй, диполи атомные. Если в каком-то веществе есть электрическое поле, то электроны и протоны испытывают влияние противоположных сил и смещаются друг относительно друга. В изоляторе электроны не могут сильно разойтись, им мешает притяжение ядра. И все же они как-то смещаются. Так что, хотя атом (или молекула) и остается нейтральным, во внешнем электрическом поле все же возникает еле заметное разделение положительных и отрицательных зарядов, и атом становится микроскопическим диполем. Если нам нужно знать поле этих атомных диполей поблизости от предмета обычных размеров, то мы имеем дело с расстояниями, большими по сравнению с промежутками между зарядами.