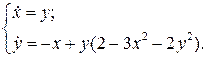Методы доказательства существования цикла

Рассмотрим систему

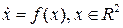. (6.1)

Будем считать, что для этой системы везде в 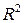выполнены условия теоремы существования и единственности решения и имеет место непрерывная зависимость решений от начальных данных. Все эти условия, например, выполнены, если правая часть системы есть дифференцируемая функция везде в .

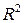Принцип кольца

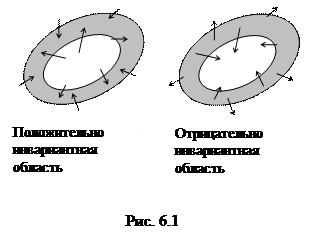Пусть на плоскости имеется замкнутая кольцеобразная область, ограниченная двумя замкнутыми гладкими кривыми g₁ и g₂ (g₁ и g₂ не являются траекториями системы (6.1)) , такая, что все траектории системы (6.1) входят вовнутрь этой области с ростом t и в дальнейшем не покидают ее (или входят в эту область при убывании t и не покидают ее при 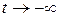). Такая область называется положительно (отрицательно) инвариантной для траекторий системы (рис. 6.1).

Лемма 6.1.Если внутри положительно (отрицательно) инвариантной для траекторий системы (6.1) области нет состояний равновесия системы, то в этой области содержится по крайней мере один цикл системы (6.1).

Существование циклов у систем с единственным положением
равновесия

Теорема 6.1.Если все собственные значения матрицы Якоби 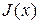системы (6.1) при 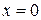имеют положительные вещественные части и система диссипативна, то она имеет по крайней мере один цикл.

Критерии диссипативности

Теорема 6.2.Система 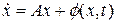с гурвицевой матрицей А и ограниченной функцией 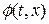диссипативна по Левинсону.

Теорема 6.3.Пусть 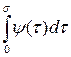ограничен при всех 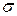и матрица A гурвицева. Тогда система 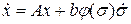( 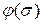– скалярная функция переменной 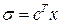, 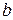и с – n-векторы.) диссипативна.

Теорема 6.3. Пусть на множестве 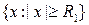определена неотрицательная дифференцируемая функция 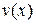, обладающая следующими свойствами:

1) ,

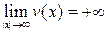2) 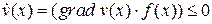при ,

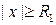3) среди решений 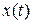системы (2.7.8) не существует таких, для которых 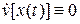при .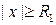

Тогда система (6.1) диссипативна.

Проиллюстрируем на примерах применение леммы 6.1 и теоремы 6.1 для доказательства существования циклов.

Пример 1.Доказать, что система

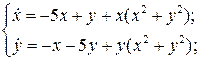(6.2)

имеет цикл.

Покажем, что система (6.2) имеет единственное состояние равновесия :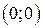

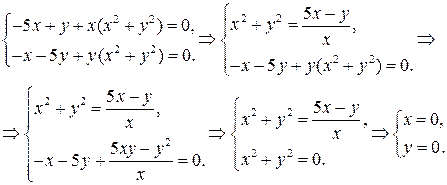
Рассмотрим функцию 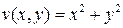. Ее производная в силу системы (6.2) имеет вид 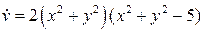. Рассмотрим две концентрические окружност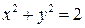и и 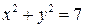. На первой из них выполнено условие 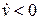, а на второй 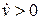. Поэтому траектории системы пересекают первую окружность по направлению «к центру», а вторую – по направлению «от центра».

Значит, в фазовом пространстве рассматриваемой системы имеется отрицательно инвариантное кольцо (рис. 6.1), в котором нет точек покоя системы. Согласно лемме 6.1, такая система имеет цикл.

На приведенном ниже рис. 6.1. изображен цикл системы (6.2), найденный путем численного интегрирования, а также траектории, навивающиеся на этот цикл при 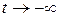изнутри и снаружи.

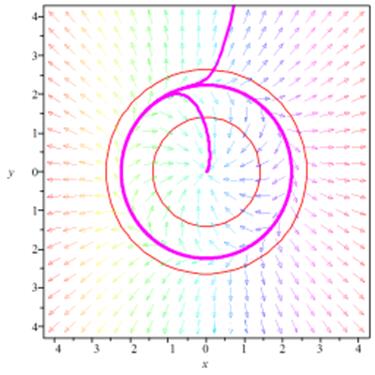
Рис. 6.2. Численное интегрирование системы (6.2)

Пример 2.Доказать, что уравнение 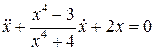имеет цикл.

Решение:

Запишем данное уравнение в виде эквивалентной системы в 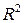, сделав замену :

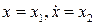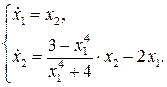(6.3)

Покажем, что система (6.3) имеет единственное неустойчивое состояние равновесия :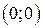

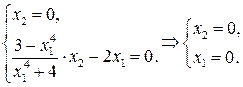
Составим якобиан системы и найдем его значение в точке .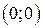

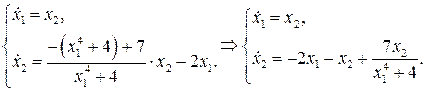
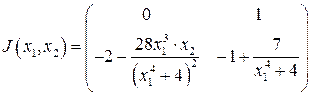
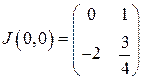
Составим характеристическое уравнение системы:

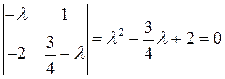
Оба корня характеристического уравнения имеют положительные вещественные части.

Значит, система (6.3) имеет единственное неустойчивое состояние равновесия .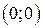

Докажем, что система диссипативна.

Очевидно, что систему можно записать в ви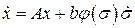де , где .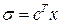

, , , .

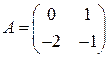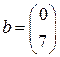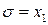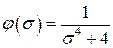Характеристический полином линейной части системы 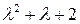гурвицев.

Докажем ограниченность интеграла .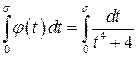

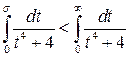
Интеграл 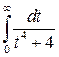сходится, так как выполнено условие .

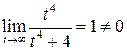Значит, система (6.3) диссипативна согласно теореме 6.3.

Таким образом, по теореме 6.1 система (6.4)по крайней мере один цикл.

На рис. 6.3 представлены результаты численного интегрирования системы (6.3).

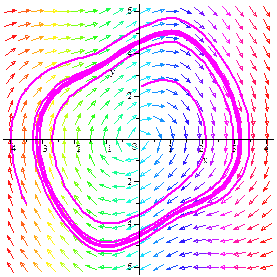
Рис. 6.3. Численное интегрирование системы (6.3)

Пример 3.Доказать, что система

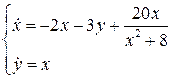(6.4)

имеет цикл.

Решение:

Покажем, что система (6.4) имеет единственное неустойчивое состояние равновесия :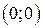

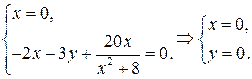
Составим якобиан системы и найдем его значение в точке .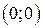

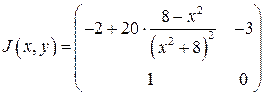
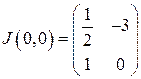
Составим характеристическое уравнение системы:

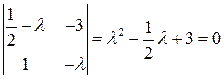
Оба корня характеристического уравнения имеют положительные вещественные части.

Значит, система имеет единственное неустойчивое состояние равновесия .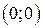

Докажем, что система диссипативна.

Система имеет вид 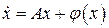. Матрица A для рассматриваемой системы имеет вид 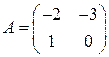. Ее характеристический полином 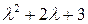гурвицев, а функция 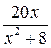ограничена.

Значит, система диссипативна согласно теореме 6.2.

Таким образом, все собственные значения матрицы Якоби 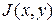системы в точке 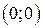имеют положительные вещественные части и система диссипативна, следовательно, она имеет по крайней мере один цикл.

На рис. 6.4 представлены результаты численного интегрирования системы (6.4).

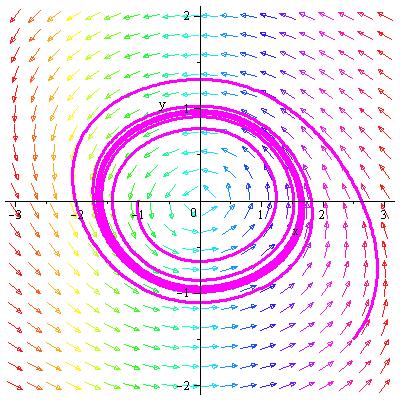
Рис. 6.4. Численное интегрирование системы (6.4)

Задание 6

Используя теорему Пуанкаре-Бендиксона, доказать существование цикла у уравнения или системы

1.

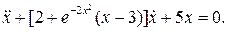
2.

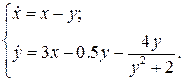
3.

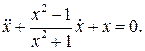
4.

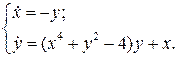
5.

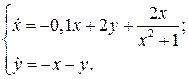
6.

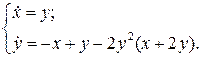
7.

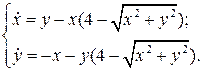
8.

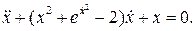
9.

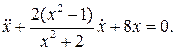
10.

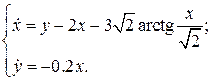
11.

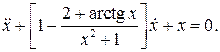
12.

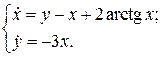
13.

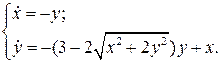
14.

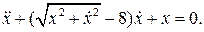
15.

16.

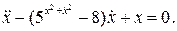
17.

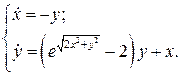
18.

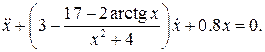
19.

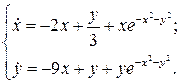
20.

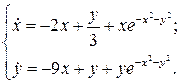
21.

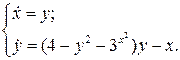
22.

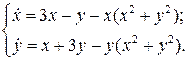
23.

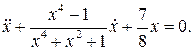
24.

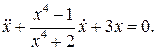
25.

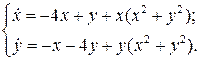
26.

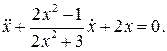
27.

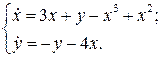
28.

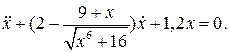
29.

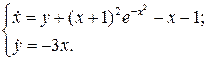
30.

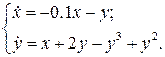
31.