Примеры решения задач

Задача 1. Симплексный метод. Торговое предприятие реализует 2 группы товаров: А и В. Нормы затрат ресурсов на каждый тип товаров, лимиты ресурсов, а также доход на единицу каждой продукции заданы в таблице. Определить плановый объем продаж и структуру товарооборота так, чтобы доход торгового предприятия был максимален.

Виды ресурсов	Норма затрат ресурсов на 1 ед. товара	Лимит ресурсов
Товары группы А	Товары группы В
Рабочее время продавцов, чел.-час	0,2
Площадь торговых залов, м2	0,5	0,1
Площадь складских помещений, м2
Накладные расходы, руб.	5
Доход на ед. продукции, руб.

РЕШЕНИЕ:

I Построим экономико-математическую модель задачи:

1) Переменные – ресурсы, ед.

1. х₁ – товары группы А, ед.

2. х₂ – товары групп В, ед.

2) Ограничения:

1. По использованию рабочего времени, Чел.-ч.: 0,2х₁+3х₂ 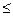24

2. По имеющейся площади торговых залов, кв.м..: 0,5х₁+0,1х₂ 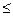5

3. По имеющейся площади складских помещений, кв. м.: 3х₁+х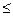₂ 32

4. По накладным расходам, руб.: 5х₁+4х₂ 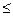75

3) Критерий оптимальности – максимальный доход торгового предприятия.

Целевая функция: Z=4х₁+3х₂ → max

4) Условие неотрицательности:

хj 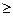0, j=1,2

II Приведем задачу к каноническому виду:

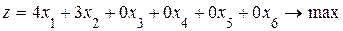
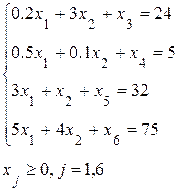
Решим ее симплексным методом аналитически.

Составляем симплексную таблицу. Перечислим по столбцам содержание таблицы:

Базис – содержит перечень базисных переменных;

С – значения коэффициентов базисных переменных в целевой функции;

План – значения базисных переменных

x₁ – x₆ – коэффициенты переменных в системе ограничений.

На первоначальном этапе в базис входят все фиктивные переменные. Тогда, учитывая, что x₁ = x₂ =0, из системы ограничений находим значения базисных переменных, заносим их в столбец План. Заполняем столбцы С и x₁, x₂ , x₃ , x₄ , x₅ , x₆. В последней строке выпишем значения - на первом этапе это значения коэффициентов целевой функции, взятые с противоположным знаком.

Очевидно, что если базис состоит только из фиктивных переменных, то значение целевой функции равно нулю. Будем последовательно улучшать опорный план, на каждом шаге вводя в базис новую переменную, и выводя из него одну базисную переменную. Процесс решения задачи закончится тогда, когда среди чисел 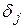не останется отрицательных.

Поскольку в первой таблице 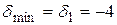, то вводиться в базис будет переменная x₁. Столбец, соответствующий переменной x₁, будем называть разрешающим, обозначим его номер 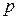. Рассчитаем значения столбца 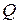по формуле:

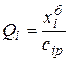, где 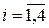- номер строки, 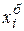- значение базисной переменной, соответствующей 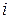-той строке, 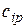- значение в ячейке таблицы, находящейся на пересечении 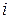-той строки с разрешающим столбцом.

Выбираем среди чисел столбца 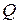минимальное положительное число. Строку, в которой это число находится, условимся называть разрешающей, а элемент, стоящий на пересечении разрешающего столбца и разрешающей строки – разрешающим элементом. Обозначим номер разрешающей строки 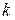. В нашем случае разрешающей строкой является строка, соответствующая переменной x₄, следовательно, эта переменная выходит из базиса.

Переход к новой симплексной таблице осуществляется по следующему алгоритму:

1. элементы разрешающей строки делятся на разрешающий элемент: , .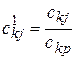

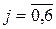2. все остальные элементы таблицы (кроме столбцов С и ), пересчитываем по формуле: 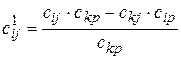, 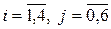. Здесь подразумевается, что столбец с номером 0 – это столбец значений базисных переменных.

Получим новую таблицу. Значение целевой функции рассчитывается как сумма произведений значений базисных переменных на их коэффициенты, т.е. сумма произведений соответствующих элементов столбцов БП и С.

Продолжая аналогично, получим решение задачи.

1 симплексная таблица
Базис	С	План							Q
x1	x2	x3	x4	x5	x6
x3			0,2
x4			0,5	0,1
x5									10.67
x6
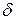			-4	-3
2 симплексная таблица
Базис	С	БП	x1	x2	x3	x4	x5	x6	Q
x3				2,96		-0,4			-55
x1				0,2
x5				0,4		-6
x6						-10			8.33
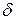				-2,2
3 симплексная таблица
Базис	С	БП	x1	x2	x3	x4	x5	x6	Q
x3		7,2					-7,4		0.164
x1							-0,5		1.8
x2						-15	2,5		-0.33
x6							-7,5		0.29
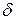						-25	5,5
4 симплексная таблица
Базис	С	БП	x1	x2	x3	x4	x5	x6	Q
x4		0,16			0,23		-0,17		-
x1		8,18			-0,11		0,34		-
x2		7,45			0,34		-0,02		-
x6		4,27			-0,79		-1,61		-
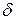		55,09			0,57		1,29

Итак, для получения максимального дохода торгового предприятия равной 55,09 руб., необходимо реализовать: товара группы А – 8,18 ед., группы В – 7,45. Дополнительные переменные х3, х4, х5, х6 показывают разницу между запасами ресурсов каждого вида и их потреблением. При оптимальном плане реализации продукции х4 = х6 = 0, т.е. остатки ресурсов площади торговых залов и накладных расходов равны нулю, а остатки рабочего времени продавцов и площади складских помещений равны соответственно 0,57чел.-ч. и 1,29 кв.м.