Постановлением Государственного комитета СССР по стандартам от 06.03.80 № 1035 срок введения установлен

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

ИССЛЕДОВАТЕЛЬСКИЕ ИСПЫТАНИЯ

ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ

ГОСТ 24026-80

ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО УПРАВЛЕНИЮ КАЧЕСТВОМ ПРОДУКЦИИ И СТАНДАРТАМ

Москва

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

ИССЛЕДОВАТЕЛЬСКИЕ ИСПЫТАНИЯ Планирование эксперимента. Термины и определения Research tests. Experiment planning. Terms and definitions

ГОСТ 24026-80

Постановлением Государственного комитета СССР по стандартам от 06.03.80 № 1035 срок введения установлен

с 01.01.81

Настоящий стандарт устанавливает термины и определения основных понятий в области исследовательских испытаний, относящихся к разделу планирования эксперимента.

Термины, установленные настоящим стандартом, обязательны для применения в нормативно-технической документации, учебниках, учебных пособиях, технической и справочной литературе в области планирования эксперимента.

Для каждого понятия установлен один стандартизованный термин. Встречающиеся в литературе термины-синонимы приведены в стандарте как недопустимые и обозначены пометкой «Ндп». Для отдельных терминов приведены краткие формы, которые разрешается применять в случаях, исключающих возможность их различного толкования.

Стандартизованные термины набраны полужирным шрифтом, краткая форма-светлым, а нерекомендуемые-курсивом.

В случаях, когда существенные признаки понятия содержатся в буквальном значении термина, определение не приведено и соответственно в графе «определение» поставлен прочерк.

В стандарте приведен алфавитный указатель содержащихся в нем терминов.

В справочном приложении даны примеры и пояснения к некоторым терминам.

Термин	Определение
1. ОСНОВНЫЕ ПОНЯТИЯ
1. Эксперимент	Система операций, воздействий и (или) наблюдений, направленных на получение информации об объекте при исследовательских испытаниях
2. Опыт	Воспроизведение исследуемого явления в определенных условиях проведения эксперимента при возможности регистрации его результатов
3. План эксперимента	Совокупность данных, определяющих число, условия и порядок реализации опытов
4. Планирование эксперимента	Выбор плана эксперимента, удовлетворяющего заданным требованиям
5. Фактор Ндп. Параметр	Переменная величина, по предположению влияющая на результаты эксперимента
6. Уровень фактора	Фиксированное значение фактора относительно начала отсчета
7. Основной уровень фактора	Натуральное значение фактора, соответствующее нулю в безразмерной шкале
8. Нормализация факторов	Преобразование натуральных значений факторов в безразмерные
9. Априорное ранжирование факторов	Метод выбора наиболее важных факторов, основанный на экспертной оценке
10. Размах варьирования фактора	Разность между максимальным н минимальным натуральными значениями фактора в данном плане
11. Интервал варьирования фактора	Половина размаха варьирования фактора
12. Эффект взаимодействия факторов	Показатель зависимости изменения эффекта одного фактора от уровней других факторов
13. Факторное пространство	Пространство, координатные оси которого соответствуют значениям факторов
14. Область экспериментирования Область планирования	Область факторного пространства, где могут размещаться точки, отвечающие условиям проведения опытов
15. Активный эксперимент	Эксперимент, в котором уровни факторов в каждом опыте задаются исследователем
16. Пассивный эксперимент	Эксперимент, при котором уровни факторов в каждом опыте регистрируются исследователем, но не задаются
17. Последовательный эксперимент Ндп. Шаговый эксперимент	Эксперимент, реализуемый в виде серий, в котором условия проведения каждой последующей серии определяются результатами предыдущих
18. Отклик Ндп. Реакция Параметр	Наблюдаемая случайная переменная, по предположению, зависящая от факторов
19. Функция отклика	Зависимость математического ожидания отклика от факторов
20. Оценка функции отклика	Зависимость, получаемая при подстановке в функцию отклика оценок значений ее параметров
21. Дисперсия оценки функции отклика	Дисперсия оценки математического ожидания отклика в некоторой данной точке факторного пространства
22. Поверхность отклика Ндп. Поверхность регрессии	Геометрическое представление функции отклика
23. Поверхность уровня функции отклика	Геометрическое место точек в факторном пространстве, которому соответствует некоторое фиксированное значение функции отклика
24. Область оптимума	Область факторного пространства в окрестности точки, в которой функция отклика достигает экстремального значения
25. Рандомизация плана	Один из приемов планирования эксперимента, имеющий целью свести эффект некоторого неслучайного фактора к случайной ошибке
26. Параллельные опыты	Рандомизированные во времени опыты, в которых уровни всех факторов сохраняются неизменными
27. Временный дрейф	Случайное или неслучайное изменение функции отклика во времени
2. МОДЕЛИ, ПЛАНЫ, МЕТОДЫ
28. Модель регрессионного анализа Регрессионная модель	Зависимость отклика от количественных факторов и ошибок наблюдения отклика
29. Модель регрессионного анализа, линейная по параметрам Ндп. Линейная модель	Модель регрессионного анализа, в которой функция отклика есть линейная комбинация базисных функций от факторов
30. Полиномиальная модель регрессионного анализа Полиномиальная модель	Модель регрессионного анализа, линейная по параметрам, задаваемая полиномом по факторам
31. Модель регрессионного анализа первого порядка Линейная модель	Модель регрессионного анализа, задаваемая полиномом первого порядка по факторам
32. Модель регрессионного анализа второго порядка Квадратичная модель	Модель регрессионного анализа, задаваемая полиномом второго порядка по факторам
33. Модель дисперсионного анализа	Зависимость отклика от качественных факторов и ошибок наблюдений отклика
34. Адекватность математической модели Адекватность модели	Соответствие математической модели экспериментальным данным по выбранному критерию
35. Коэффициент регрессии	Параметр модели регрессионного анализа
36. Блок плана	Часть плана, включающая опыты, условия проведения которых однородны с точки зрения значений одного или нескольких мешающих факторов
37. Точка плана	Упорядоченная совокупность численных значений факторов, соответствующая условиям проведения опыта
38. Центральная точка плана Центр плана	Точка плана, соответствующая нулям нормализованной (безразмерной) шкалы по всем факторам
39. Звездная точка плана	Точка плана второго порядка, лежащая на координатной оси в факторном пространстве
40. Звездное плечо	Расстояние между центральной и звездной точками плана второго порядка
41. Спектр плана	Совокупность всех точек плана, отличающихся уровнями хотя бы одного фактора
42. Матрица плана	Стандартная форма записи условий проведения экспериментов в виде прямоугольной таблицы, строки которой отвечают опытам, столбцы-факторам
43. Матрица спектра плана	Матрица, составленная из всех строк матрицы плана, отличающихся уровнями хотя бы одного фактора
44. Матрица дублирования	Квадратная диагональная матрица, диагональные элементы которой равны числам параллельных опытов в соответствующих точках спектра плана
45. Матрица базисных функций модели	Матрица, задающая численные значения базисных функций линейной по параметрам модели в опытах реализуемого плана
46. Усеченная матрица базисных функций модели	Подматрица матрицы базисных функций модели, содержащая строки, отвечающие спектру плана
47. Матрица моментов плана	Квадратичная симметричная матрица, элементы которой есть скалярные произведения соответствующих векторов-столбцов матрицы базисных функций
48. Информационная матрица плана	Нормированная матрица моментов плана
49. Полный факторный план	План, содержащий все возможные комбинации всех факторов на определенном числе уровней равное число раз
50. Дробный факторный план Дробная реплика полного факторного плана	План, содержащий часть комбинаций полного факторного плана
51. Генератор плана	Алгебраическое выражение, используемое при построении дробного факторного плана
52. План эксперимента первого порядка Линейный план	План с двумя или более уровнями факторов, позволяющий найти раздельные оценки параметров регрессионной модели первого порядка
53. План взвешивания	План первого порядка, включающий факторы на двух или трех уровнях
54. Симплекс-план	План эксперимента первого порядка, точки которого размещаются в вершинах симплекса
55. План эксперимента второго порядка	План с более чем двумя уровнями факторов для нахождения оценок параметров регрессионной модели второго порядка
56. План дисперсионного анализа	План с дискретными уровнями факторов для нахождения оценок параметров дисперсионной модели
57. Латинский квадрат	План дисперсионного анализа, задаваемый расположением некоторого числа символов в ячейках, сгруппированных в строки и столбцы так, что каждый символ встречается один раз в каждой строке и в каждом столбце
58. Латинский куб первого порядка Латинский куб	План дисперсионного анализа, задаваемый расположением некоторого числа символов в квадратах из строк и столбцов так, что каждый символ встречается одинаковое число раз в каждом квадрате
59. Критерий оптимальности плана	-
60. Ортогональность плана	Свойство плана, при котором матрица моментов для заданной модели является диагональной
61. Ротатабельность плана	Свойство плана, при котором дисперсия оценки функции отклика зависит только от расстояния от центра плана
62. Композиционность плана	Свойство плана, позволяющее выполнять эксперимент последовательно, переходя от более простых моделей к более сложным
63. Насыщенность плана	Свойство плана, задающееся разностью между числом точек спектра плана и числом оцениваемых параметров модели
64. Метод случайного баланса Случайный баланс	Метод отсеивания факторов, основанный па использовании сверхнасыщенных планов со случайным выбором сочетаний уровней факторов
65. Метод крутого восхождения	Метод экспериментальной оптимизации, сочетающий полный или дробный факторный эксперимент с движением по градиенту функции отклика
66. Эволюционное планирование эвоп	Метод экспериментальной оптимизации, сочетающий многократное использование дробных и полных факторных планов с движением по градиенту функции отклика и предназначенный для совершенствования производственных объектов
67. Последовательный симплексный метод псм	Метод экспериментальной оптимизации, основанный на сочетании насыщенного плана, заданными вершинами симплекса с последовательным отражением наихудшей вершины относительно противоположной грани
68. Регрессионный анализ	Статистический метод анализа и обработки экспериментальных данных при воздействии на отклик только количественных факторов, основанный на сочетании аппарата метода наименьших квадратов и техники статистической проверки гипотез
69. Дисперсионный анализ	Статистический метод анализа и обработки экспериментальных данных при воздействии на отклик только количественных факторов, основанный на использовании техники статистической проверки гипотез и представлении общей вариации экспериментальных данных в виде суммы вариаций, обусловленных исследуемыми факторами и их взаимодействиями
70. Метод ковариационного анализа	Статистический метод анализа и обработки экспериментальных данных при воздействии на отклик как количественных, так и качественных факторов, основанный на сочетании элементов регрессионного и дисперсионного анализа

АЛФАВИТНЫЙ УКАЗАТЕЛЬ

Адекватность модели
Адекватность модели математической
Анализ дисперсионный
Анализ регрессионный
Баланс случайный
Блок плана
Генератор плана
Дисперсия оценки функции отклика
Дрейф временной
Интервал варьирования фактора
Квадрат латинский
Композиционность плана
Коэффициент регрессии
Критерий оптимальности плана
Куб латинский
Куб латинский первого порядка
Матрица базисных функций модели
Матрица базисных функций модели усеченная
Матрица дублирования
Матрица плана информационная
Матрица моментов плана
Матрица плана
Матрица спектра плана
Метод ковариационного анализа
Метод крутого восхождения
Метод последовательный симплексный
Метод случайного баланса
Модель дисперсионного анализа
Модель квадратичная
Модель линейная
Модель линейная
Модель полиномиальная
Модель регрессионная
Модель регрессионного анализа
Модель регрессионного анализа второго порядка
Модель регрессионного анализа, линейная по параметрам
Модель регрессионного анализа первого порядка
Модель регрессионного анализа полиномиальная
Насыщенность плана
Нормализация факторов
Область оптимума
Область планирования
Область экспериментирования
Опыт
Опыты параллельные
Отклик
Ортогональность плана
Оценка функции отклика
Параметр	5, 18
План взвешивания
План эксперимента второго порядка
План дисперсионного анализа
План линейный
План факторный дробный
План факторный полный
План эксперимента
План эксперимента первого порядка
Планирование эволюционное
Планирование эксперимента
Плечо звездное
Поверхность отклика
Поверхность регрессии
Поверхность уровня функции отклика
Пространство факторное
ПСМ
Размах варьирования фактора
Рандомизация плана
Ранжирование факторов априорное
Реакция
Реплика полного факторного плана дробная
Ротатабельность плана
Симплекс-план
Спектр плана
Точка плана
Точка плана звездная
Точка плана центральная
Уровень фактора
Уровень фактора основной
Фактор
Функция отклика
Центр плана
эвоп
Эксперимент
Эксперимент активный
Эксперимент пассивный
Эксперимент последовательный
Эксперимент шаговый
Эффект взаимодействия факторов

ПРИЛОЖЕНИЕ

Справочное

ПОЯСНЕНИЯ К ТЕРМИНАМ

К термину «Эксперимент» (п. 1)

В теории планирования эксперимента часто определяют эксперимент как совокупность условий и результатов проведения серий опытов.

К термину «План эксперимента» (п. 3)

Формально план часто можно представить в виде последовательности векторов 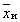, и=1, 2, . . . , n, где n-число опытов в плане, а компоненты 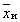„ определяют условия каждого опыта.

К термину «Планирование эксперимента» (п. 4)

В широком смысле слова планирование эксперимента-научная дисциплина, занимающаяся разработкой и изучением оптимальных программ проведения экспериментальных исследований.

К термину «Фактор» (п. 5)

В большинстве моделей, используемых в планировании эксперимента, предполагается, что факторы могут рассматриваться как детерминированные переменные. Обычно факторы выражаются в безразмерных единицах масштаба иобозначаются буквами x_i, i = 1, 2, . . ., k. Совокупность факторов изображается вектором 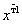= 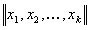. Здесь и далее векторы обозначаются малыми полужирными буквами, матрицы-большими полужирными.

¹ Символ «Т» обозначает операцию транспортирования.

К термину «Уровень фактора» (п. 6)

Факторы могут различаться по числу уровней, на которых возможно их фиксировать в данной задаче. Фактор, варьируемый на р уровнях, называют р-уровневым фактором.

К термину «Основной уровень фактора» (п. 7)

Основной уровень фактора, обозначаемый 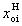, где индекс i относится к номеру фактора, служит для фиксирования в области планирования таких условий эксперимента, которые представляют наибольший интерес для исследователя в данный момент, и относится к определенному плану эксперимента.

К термину «Нормализация факторов» (п. 8)

За единицу масштаба безразмерной системы координат принимается некоторый интервал в натуральных единицах. При нормализации фактора наряду с изменениями масштаба изменяется начало отсчета. Значение i-го фактора в безразмерной системе связано со значением этого фактора 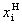в натуральной системе (в именованных единицах) формулой

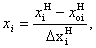
где 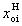-основной уровень фактора, принимаемый за начало отсчета;

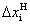-интервал в натуральных единицах масштаба, соответствующий одной единице масштаба в безразмерных переменных.

С геометрической точки зрения нормализация факторов равноценна линейному преобразованию пространства факторов, при котором производится перенос начала координат в точку, отвечающую основным уровням, и сжатие-растяжение пространства в направлении координатных осей.

К термину «Априорное ранжирование факторов» (п. 9)

Метод основан на упорядочении экспертами множества факторов по убыванию (или возрастанию) их важности, суммирование рангов факторов и выборе факторов путем рассмотрения суммарного ранжирования.

К термину «Размах варьирования фактора» (п. 10)

Указывает границы области варьирования данного фактора в данном эксперименте.

К термину «Интервал варьирования фактора» (п. 11)

Интервал или шаг варьирования фактора, обозначаемый 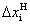, для фактора с номером i служит для перехода от натурального масштаба к безразмерному. Вместе с основным уровнем он задает область действия для данного плана, т. е. область действия есть 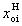± 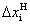или иначе

( + ; - ).

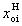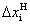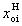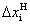К термину «Эффект взаимодействия факторов» (п. 12)

В полиномиальном уравнении регрессии эффект взаимодействия выражается параметром при членах, включающих произведения факторов. Различаются парные взаимодействия вида х_i х_j, тройные вида х_i х_j x_k и более высокого порядка.

К термину «Факторное пространство» (п. 13)

Размерность факторного пространства равна числу факторов k. Каждой точке факторного пространства соответствует вектор

= .

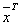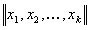К термину «Область экспериментирования» (п. 14)

Если область планирования задается интервалами возможного изменения факторов, она представляет собой гиперпараллелепипед (в частном случае куб). Иногда область планирования задается гиперсферой.

К термину «Функция отклика» (п. 19)

Функция отклика выражается соотношением

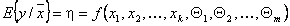
или

.

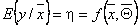Функция отклика связывает между собой математическое ожидание отклика 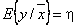, совокупность факторов, выражаемую вектором 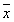, и совокупность параметров модели, определяемую вектором

.

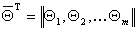Параметры модели априори неизвестны и подлежат определению из эксперимента.

На функцию отклика могут переноситься определения, связанные с моделью, например, линейная (по параметрам), полиномиальная, квадратичная и т. д.

К термину «Поверхность отклика» (п. 22)

Поверхность отклика имеет размерность k и размещена в (k+1)-мерном пространстве.

К термину «Параллельные опыты» (п. 26)

Параллельные опыты служат для получения выборочной оценки дисперсии воспроизводимости результатов эксперимента.

К термину «Временной дрейф» (п. 27)

Дрейф обычно связывают с изменением во времени каких-либо характеристик функции отклика (параметров, положения экстремальной точки и т. п.). Различают детерминированный и случайный дрейфы. В первом случае процесс изменения параметров (или иных характеристик функции отклика) описывается детерминированной (обычно степенной) функцией времени. Во втором случае изменение параметров-случайный процесс. Если дрейф аддитивный, то поверхность отклика смещается во времени, не деформируясь (при этом дрейфует только свободный член функции отклика, т. е. член, не зависящий от значений факторов). При неаддитивном дрейфе поверхность отклика во времени деформируется. Цель планирования в условиях аддитивного дрейфа исключить влияние дрейфа на оценки эффектов факторов. При дискретном дрейфе это удается сделать путем разбиения эксперимента на блоки. При непрерывном дрейфе используют планы эксперимента, ортогональные к дрейфу, описываемому степенной функцией известного вида.

В задачах экспериментальной оптимизации в условиях дрейфа функции отклика применяют методы адаптационной оптимизации, к которым относятся метод эволюционного планирования и последовательный симплексный метод.

К термину «Модель регрессионного анализа» (п. 28)

Модель регрессионного анализа выражается соотношением

,

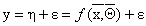где 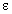-случайная ошибка. Для некоторого и-го наблюдения имеем

,

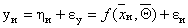Наиболее простые предположения о случайных величинах e_и состоят в том, что их математические ожидания равны нулю

E{e_и}=0,

дисперсии постоянны

,

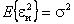а ковариации равны нулю

E{e_и e_v}=0, и¹v.

Последние условия соответствуют равноточности и некоррелированности наблюдений.

К термину «Модель регрессионного анализа, линейная по параметрам» (п. 29)

Линейная по параметрам модель регрессионного анализа представимав форме

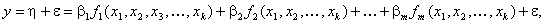
где b₁-параметры модели, i = l, 2, . . . , т;

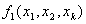-известные базисные функции переменных 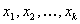(факторов), не зависящие от параметров модели.

Линейная модель может быть записана более лаконично

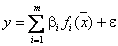
или

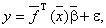
где 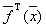-вектор-строка базисных функций (базисная вектор-функция)

,

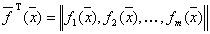b-вектор параметров модели

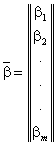
К термину «Модель регрессионного анализа первого порядка» (п. 31)

Модель первого порядка может содержать свободный член-дополнительный параметр; при этом обозначать параметры модели индексами, начиная с нуля

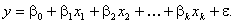
Иногда при обозначении модели первого порядка используется фиктивная переменная, тождественно равная единице:

x₀=1.

С учетом этого обозначения модель может быть записана в виде суммы

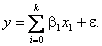
К термину «Модель регрессионного анализа второго порядка» (п. 32)

Модель регрессионного анализа второго порядка для факторов в общем случае содержит 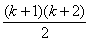параметров. Параметры модели чаще всего нумеруют не подряд от 1 до 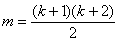, а начиная с нуля и в соответствии с индексами независимых переменных, на которые умножаются параметры. Наиболее распространенная форма записи квадратичной модели следующая

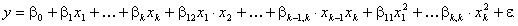
К термину «Модель дисперсионного анализа» (п. 33)

Модель вида

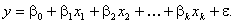
где х₁- дискретные переменные, обычно целочисленные (часто х_i, либо 0, либо 1).

Наиболее простые предположения о случайных величинах те же, что и для модели регрессионного анализа.

Неизвестные параметры дисперсионной модели могут быть детерминированными или случайными величинами. В первом случае, модель называют моделью с постоянными факторами или моделью 1. Модель, в которой все параметры b_i (может быть за исключением одного) являются случайными величинами, называется моделью со случайными факторами или моделью II.

В промежуточных случаях модель называется смешанной.

К термину «Адекватность математической модели» (п. 34)

Для проверки адекватности модели часто используют F-критерий Фишера.

К термину «Коэффициент регрессии» (п. 35)

Под коэффициентом регрессии обычно понимают параметры регрессионной модели, линейной по параметрам. Их чаще всего обозначают буквой b.

К термину «Блок плана» (п. 36)

Чтобы исключить воздействие на оценки эффектов факторов каких-либо источников неоднородности, план разбивают на блоки. Различают полноблочные планы, в которых в каждом блоке реализуется одна и та же совокупность опытов, и неполноблочные, когда блоки состоят из различных комбинаций опытов. Неполноблочные планы бывают сбалансированными и частично-сбалансированными (сбалансированные неполные блок-схемы и частично-сбалансированные неполные блок-схемы соответственно).

К термину «Точка плана» (п. 37)

Точке плана с номером и в факторном пространстве отвечает вектор

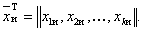
К термину «Центральная точка плана» (п. 38)

Набор основных уровней всех факторов образует вектор-точку в факторном пространстве, которая и называется центральной точкой плана:

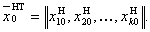
К термину «Матрица плана» (п. 42)

Матрица плана имеет размеры (N´k), она может иметь совпадающие строки;

(i, j)-элемент матрицы плана равен уровню j-го фактора в i-м опыте.

К термину «Матрица спектра плана» (п. 43)

Все строки матрицы спектра плана различны, ее размеры (n´k),

где n-число точек в спектре плана.

К термину «Матрица дублирования» (п. 44)

Матрица дублирования имеет вид

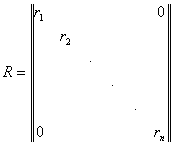
Примечание. План эксперимента может быть задан либо матрицей плана, либо матрицей спектра плана в совокупности с матрицей дублирования.

К термину «Матрица базисных функций модели» (п. 45)

Матрица базисных функций модели состоит из N строк т столбцов. Элементами i-й строки такой матрицы являются значения базисных функции в i-м опыте.

Матрица базисных функций имеет вид

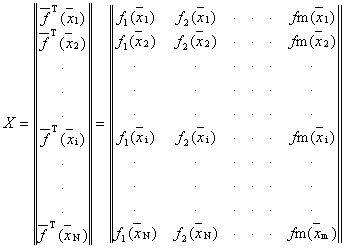
К термину «Усеченная матрица базисных функций модели» (п. 46)

Усеченная матрица базисных функций модели содержит набор различающихся между собой строк матрицы Х, следовательно она имеет размеры (п´т)

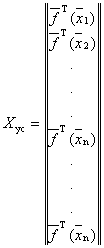
К термину «Матрица моментов плана» (п. 47)

Это определение справедливо при обычных предположениях регрессионного анализа (о равноточности и некоррелированности наблюдений отклика). Матрица моментов имеет размеры (m´m) и может быть выражена

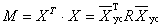
или

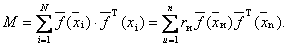
В общем случае при неравноточных и коррелированных откликах матрица моментов может быть выражена:

,

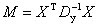где D_y- ковариационная матрица вектора наблюдений.

К термину «Информационная матрица плана» (п. 48)

Матрица моментов, каждый элемент которой поделенна число опытов в плане.

К термину «Полный факторный план» (п. 49)

Факторный план характеризуется наличием ряда факторов, каждый из которых варьируется на двух или более уровнях. Многие типы планов можно интерпретировать как частные случаи факторных планов.

К термину «Дробный факторный план» (п. 50)

Различают регулярные и нерегулярные дробные факторные планы (дробные реплики). Регулярность реплики означает сохранение в ее структуре некоторых важных характеристик полного плана, например, симметрии и ортогональности.

К термину «План взвешивания» (п. 53)

Название связано с операцией взвешивания предметов на одночашечных (безмены) или двухчашечных весах. Рассматривается случай, когда действие факторов можно считать аддитивным.

К термину «Симплекс-план» (п. 54)

Симплекс-план может быть изображен в факторном пространстве в виде полного набора вершин k-мерного симплекса.

К термину «Латинский квадрат» (п. 57)

Если обозначить число символов через S, то латинский квадрат-это такая структура, где S символов расположены в S² ячейках. Символы располагаются в S строках и S столбцах так, что каждый символ встречается один и только один раз в каждой строке и в каждом столбце.

К термину «Латинский куб первого порядка»(п. 58)

Если обозначить число символов через S, то латинский куб это такая структура, где S символов расположены в S³ ячейках. Они располагаются в S квадратах из S строк и S столбцов так, что каждый символ встречается одинаковое число раз в квадрате.

К термину «Критерий оптимальности плана» (п. 59)

К числу важнейших критериев относят:

а) критерий D-оптимальности-это мера эффективности плана, сформулированная на языке свойств информационной матрицы плана.

ПустьМ=Х^T×X -матрица моментов плана, а

М_N= 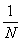Х^T×X-информационная матрица плана.

Здесь N-общее число опытов в плане, Х-матрица базисных функций для заданной модели и фиксированного плана, Х^T-транспонированная матрица X. Удовлетворение требования D-оптимальностп означает минимизацию определителя матрицы 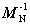( 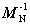матрица, обратная информационной матрице М_N) на множестве элементов х_ij матрицы плана, т. е.

min det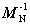

.

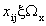Здесь х_ij-элемент i-й строки и j-го столбца матрицы плана, i=l, 2, . . . , N, j=1, . . . , k (k-число факторов). W_х-область экспериментирования. det-обозначение операции вычисления определителя матрицы.

D- оптимальный план минимизирует на множестве допустимых планов обобщенную дисперсию оценок коэффициентов регрессии;

б) критерий А-оптимальности-это мера эффективности плана, сформулированная на языке свойств информационной матрицы плана.

Пусть М=Х^T×X-матрица моментов плана, а

М_N= 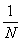Х^T×X-информационная матрица плана.

Здесь N-общее число опытов в плане, Х-матрица базисных функций для заданной модели и фиксированного плана, Х^T-транспонированная матрица X. Удовлетворение требования A-оптимальности означает минимизацию следа матрицы 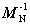на множестве элементов х_ij матрицы плана, т. е.

min S_p ,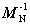

.

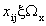где S_p-обозначение операции вычисления следа матрицы;

х_ij-элемент i-й строки и j-го столбца матрицы плана, (i=l, 2, . . . , N, j=1, 2, . . . , k);

W_х-область экспериментирования.

А-оптимальный план минимизирует на множестве допустимых планов среднюю дисперсию оценок коэффициентов регрессии.

В настоящее время используется свыше 20 различных критериев оптимальности планов.

К термину «Ротатабельность плана» (п. 61)

Планирование является ротатабельным, если матрица моментов плана инвариантна к ортогональному вращению координат.

К термину «Насыщенность плана» (п. 63)

Различают ненасыщенные планы, когда разность равна нулю, и перенасыщенные (сверхнасыщенные) планы, когда разность отрицательна.

К термину «Метод случайного баланса» (п. 64)

Случайный баланс использует нерегулярную дробную реплику от полного факторного плана, задающую сверхнасыщенный план для модели, включающий линейные эффекты и парные воздействия. Обработка данных основывается на методах статистического оценивания и некоторых эвристических соображениях.

К термину «Эволюционное планирование» (п. 65)

Существуют различные модификации ЭВОП: обычное ЭВОП (ЭВОП Бокса), последовательный симплексный метод, квадратичное вращаемое ЭВОП и т. п.

К термину «Дисперсионный анализ» (п. 69)

К количественным относятся такие факторы, как температура, давление, вес и т. п. примеры качественных факторов -тип прибора, вид материала, сорт зерна и т. п. Если количественный фактор принимает в эксперименте небольшое число различных значений, то его можно рассматривать как качественный. В такой ситуации применима техника дисперсионного анализа.