ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ. Лабораторная работа №3

Лабораторная работа №3

Изучение нормального распределения

Случайной величины на доске Гальтона

ЦЕЛЬ РАБОТЫ

Получение экспериментальной кривой распределения случайной величины, сравнение ее с теоретической кривой нормального рас-пределения. Расчет оценочных значений числовых параметров рас-пределения случайной величины. Изучение и экспериментальная проверка правил, применяемых при обработке результатов измере-ний.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Данная работа посвящена определению по ограниченному коли-честву опытов неизвестных параметров, от которых зависит рас-пределение случайной величины. Надо отметить, что любое значе-ние искомого параметра, вычисленное на основании ограниченного числа опытов, всегда будет содержать элемент случайности. Такое приближенное, случайное значение называется оценкой параметра. Например, оценкой для математического ожидания может служить среднее арифметическое наблюденных значений случайной вели-чины в 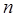независимых опытах. При очень большом числе опытов среднее арифметическое будет с большой вероятностью весьма близким к математическому ожиданию. Если же количество опытов 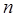невелико, то замена математического ожидания средним значе-нием приведет к некоторой ошибке. Эта ошибка будет тем больше, чем меньше число опытов. Так же будет обстоять дело и с оцен-ками других параметров. Любая из таких оценок случайна, при пользовании ею неизбежны ошибки. Желательно выбрать такую оценку, чтобы ошибки были по возможности минимальными.

Возьмем случайную величину 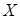, закон распределения которой содержит неизвестный параметр 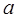. Требуется найти подходящую оценку для параметра 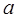по результатам 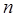независимых опытов, в которых величина 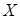принимает определенное значение. Обозна-чим наблюденные значения случайной величины:

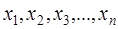. (3.3.1)

Обозначим как 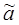оценку для параметра 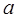. Любая оценка
должна представлять собой функцию величин :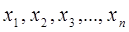

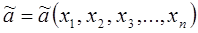. (3.3.2)

Ясно, что 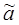сама является случайной величиной. Закон распре-деления 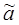зависит, во–первых, от закона распределения 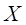, а во-вторых– от числа опытов. При этом оценка 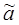должна удовлетво-рять ряду требований, чтобы быть в каком-то смысле доброка-чественной оценкой. Требование первое: оценка 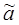при увеличении количества опытов должна приближаться к параметру 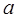. Оценка, обладающая таким свойством, называется состоятельной. Требо-вание второе: при использовании величины 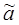вместо 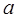, мы не должны делать систематическую ошибку в сторону завышения или занижения. Оценка, удовлетворяющая такому условию, называется несмещенной. В качестве оценки для математического ожидания, удовлетворяющей вышеприведенным требованиям, можно взять среднее арифметическое наблюдаемых значений :

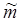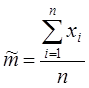. (3.3.3)

Для оценки дисперсии можно взять величину, определяемую со-гласно выражению:

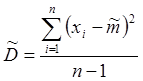. (3.3.4)

Здесь в знаменателе стоит 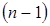, а не 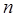, т.к. в противном слу-чае, как показывает теория, оценка дисперсии получается смещен-ной.

Мы рассмотрели вопрос об оценке неизвестного параметра од-ним числом. Такая оценка называется точечной. В ряде задач тре-буется не только найти для параметра 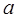подходящее численное значение, но и оценить его точность и надежность. Требуется уз-нать, к каким ошибкам приведет замена параметра 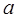его точечной оценкой 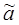и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы. Такие задачи осо-бенно актуальны при малом числе наблюдений, когда точечная оценка в значительной мере случайна и приближенная заме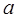на на 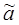может привести к серьезным ошибкам. Чтобы дать представле-ние о точности и надежности оценки 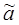, в математической статис-тике пользуются так называемыми доверительными интервалами и доверительными вероятностями.

Рассмотрим задачу о доверительном интервале для математи-ческого ожидания. Пусть произведено 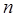независимых опытов над случайной величиной 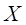, характеристики которой (математическое ожидание 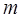и дисперсия 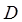) неизвестны. Для этих параметров по-лучаем оценки:

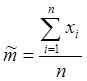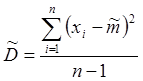; . (3.3.5)

Требуется построить доверительный интервал 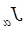, соответству-ющий доверительной вероятности 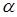для математического ожида-ния 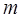величины 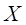. При решении этой задачи воспользуемся тем, что величина 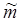представляет собой сумму 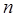независимых, одина-ково распределенных случайных величин 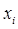, и согласно централь-ной предельной теореме при большом 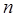ее закон распределения близок к нормальному. На практике даже при небольшом числе слагаемых (порядка 10-20) закон распределения можно приблизи-тельно считать нормальным. Будем исходить из того, что величина 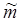распределена по нормальному закону.

Характеристики этого закона – математическое ожидание 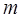и дисперсия 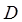. Предположим, что величина 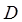нам известна, и най-дем такую величину 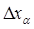, для которой

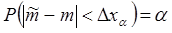. (3.3.6)

Применяя распределение Гаусса, получим:

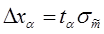, (3.3.7)

где 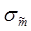– среднее квадратичное отклонение оценки ;

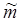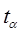– функция, определяемая из распределения Гаусса.

Дисперсия 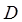, через которую выражается величина 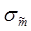, нам точно неизвестна, и в качестве ее ориентировочного значения мож-но воспользоваться приближенным, оценочным значением :

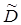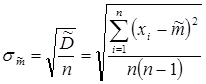. (3.3.8)

Таким образом, задача построения доверительного интервала решена:

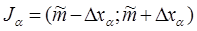. (3.3.9)

Равенство (3.3.9) означает, что неизвестное значение математи-ческого ожидания 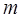попадет в интервал 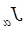с вероятностью .

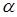При этом необходимо отметить, что ранее мы рассматривали ве-роятность попадания случайной величины в заданный интервал. Здесь дело обстоит иначе: значение математического ожидания 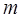– величина не случайная, зато случаен интервал 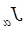. Случайно его положение на оси абсцисс, определяемое его центром 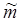; случай-на и длина интервала, равная 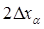, т.к. величина 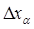вычисляет-ся, как правило, по опытным данным. Поэтому в данном случае лучше будет толковать величину 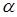не как вероятность попадания точки 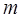в интервал 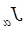, а как вероятность того, что случайный ин-тервал 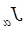накроет точку .

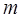Мы рассмотрели приближенный метод построения доверительно-го интервала для математического ожидания 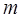. Идея точных по-строений доверительных интервалов сводится к следующему. Лю-бой доверительный интервал находится из условия, выражающего вероятность выполнения некоторых неравенств, в которые входит интересующая нас оценка 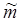. Закон распределения оценки 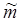зави-сит от самих неизвестных параметров величины 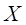. Однако иногда удается перейти от случайной величины 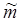к какой-либо другой функции наблюдаемых значений 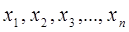, закон распределе-ния которой не зависит от неизвестных параметров, а зависит толь-ко от количества опытов 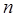и от вида закона распределения .

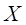Например, доказано, что при нормальном распределении вели-чины 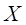случайная величина

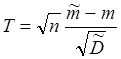, (3.3.10)

где

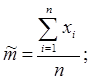
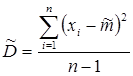(3.3.11)

подчиняется так называемому закону распределения Стьюдента. Плотность этого распределения зависит только от числа 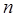. Поэто-му доверительный интервал для математического ожидания 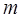можно точно определить, пользуясь распределением Стьюдента. Можно показать, что процедура определения его аналогична рас-смотренной в предыдущем случае, только вместо значения функ-ции 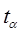, определяемой из распределения Гаусса, берутся значения функции 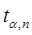, определяемой из распределения Стьюдента. Значения функции 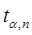обычно называют коэффициентами Стьюдента. Зна-чения 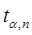определяются не только вероятностью 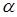, но и коли-чеством опытов 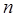. Распределением Стьюдента пользуются, в ос-новном, когда число измерений невелико, т.е. 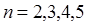. Значения функции 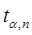являются табличной величиной, зависящей от довери-тельной вероятности 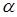и количества опытов 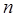(см.Приложение).