II. 1. Сила сопротивления при колебаниях подводных трубопроводов

Для оценки напряженного состояния колеблющегося подводного трубопровода необходимо установить величину и основные зависимости сил сопротивления (демпфирование, рассеяние энергии) при колебаниях. Рассеяние энергии при колебаниях подводных трубопроводов складывается из потерь на гидродинамические сопротивления, сопротивление в материале конструкции трубопровода (труба, изоляция, футеровка, бетонное покрытие, балластировка) и потерь в грунт через опоры. Гидродинамическое сопротивление, потери энергии в грунт через опоры, потерн за счет трения футеровки и балласта о поверхность трубы будем относить, как это принято в теории колебаний, к внешним источникам рассеяния энергии в отличие от внутренних источников, к которым относится рассеяние энергии в материале трубы.

Внутреннее рассеяние является функцией напряжения и скорости деформации в материале трубопровода. Существуют различные гипотезы внутреннего трения при колебаниях упругих систем, некоторые из них хорошо совпадают с результатами экспериментов, но с математической точки зрения сложны и значительно затрудняют динамический расчет.

Гидродинамическое сопротивление при колебаниях включает рассеяние энергии па вихреобразование, сопротивление трения и волновое сопротивление.

Рассеяние энергии в грунт через опоры и вследствие трения футеровки и пригрузки по аналогии с классификацией, принятой в теории колебаний механических систем, можно отнести к конструкционным потерям. Величина и расчетные зависимости конструкционных потерь для подводных трубопроводов пока еще не изучены.

Учитывая сложность аналитической оценки сил сопротивления со всеми их составляющими, авторами проведены специальные исследования в натурных условиях по определению основных факторов, влияющих на сопротивление при колебаниях трубопроводов.

На основании результатов исследований колебаний надземных и подводных магистральных трубопроводов можно сделать вывод, что при значительной длине подводного участка трубопровода потерн энергии в материале трубы, изоляции и футеровки, а также рассеяние энергии через опоры в грунт малы по сравнению с гидродинамическими потерями. Следовательно, в некоторых случаях при колебаниях подводных трубопроводов основными можно считать гидродинамические силы сопротивления.

Значительная трудность теоретического определения сил сопротивления при колебаниях подводных трубопроводов обусловливает необходимость их экспериментального исследования. Одним из проявлений рассеяния энергии является затухание колебаний, приводящее к изменению амплитуд. Закон погашения амплитуд свободных колебании характеризует функцию сил сопротивления и может быть определен по развертке собственных затухающих колебаний.

Для определения сил сопротивления применительно к колебаниям подводных трубопроводов были выполнены эксперименты в условиях плоской и пространственной задач. Для случая плоской задачи использовали жесткие модели цилиндров диаметром D=32; 51; 100 мм и длиной L=1000 мм. Эти модели закреплялись на упругих подвесах и представляли собой колебательную систему с одной степенью свободы. Для случая пространственной задачи применяли модели цилиндров: D=32/1 мм, L=4481 мм; D=33/2 мм, L=2894 мм; D=51/1,4 мм; L=3752 мм, которые закреплялись шарнирно по концам и представляли собой колебательную систему с распределенными параметрами. Колебания цилиндров соответствовали первому тону. Силы сопротивления определяли по затуханию собственных колебаний. С помощью специального устройства цилиндры выводили из положения равновесия и они совершали собственные затухающие колебания. Частота и амплитуда колебаний измерялись тензорезисторами, наклеенными на упругие подвесы, и через усилитель ТА5 регистрировались осциллографом Н700.

В опытах наряду с силами гидродинамического сопротивления учитывались и силы сопротивления в элементах закреплений и упругих подвесах моделей. Декремент колебаний, характеризующий гидродинамические силы сопротивления δг, определяли по формуле

δ_г = δ - δ₁ (3)

где δ —декремент колебаний с учетом всех сил сопротивления (гидродинамические, конструкционные, в материале цилиндра); δ1—декремент колебаний, соответствующий конструкционным силам сопротивления и рассеянию энергии в материале цилиндра.

Значения δ определяли по колебаниям цилиндров в воде, δ1 — по колебаниям тех же цилиндров в воздухе.

В формуле (5.10) δ и δ1, соответствовали одинаковой амплитуде колебаний. В экспериментах имело место интенсивное затухание свободных колебаний цилиндров, поэтому декременты колебаний определяли по формуле

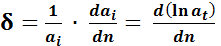(4)

где dai/dn — интенсивность убывания амплитуды колебаний вдоль оси циклов п затухающих колебаний. 

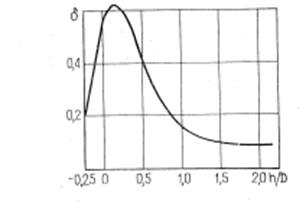
Рис. 2 Зависимость декремента колебаний δ

Результаты опытов показывают, что при отсутствии влияния дна и свободной поверхности декремент колебании δг несущественно зависит от амплитуды колебаний, и поэтому в практических расчетах гидродинамические силы сопротивления при колебаниях можно считать линейно зависящими от скорости перемещения. Декремент колебаний δг значительно зависит от расположения трубопровода относительно свободной поверхности при h/D<1,5 (рис. 2).

При изменении h/D от 1,5 до 0,15 δг возрастает от 0,1 до 0.62÷0,82. Такое повышение δг объясняется увеличением волновой составляющей гидродинамического давления, которая сдвинута относительно перемещения трубопровода по фазе на π/2 и действует в одной фазе с силами гидродинамического сопротивления. Как показывают результаты экспериментов, с уменьшением h/D<1,5 возрастает влияние составляющих гидродинамического давления, эквивалентных силам сопротивления (увеличивается «присоединенное трение»), и уменьшается влияние составляющих гидродинамического давления, эквивалентных инерционному воздействию (уменьшается коэффициент присоединенной массы μ). С уменьшением относительного расстояния трубопровода от дна s/D до 0,5 отмечено незначительное уменьшение декремента колебании δг.

При расположении трубопровода в подводной траншее величина δг зависит от крутизны откоса траншеи и относительной ширины траншеи по дну bT/D.

Рассмотренные выше значения и зависимости для декрементов колебаний можно использовать в динамических расчетах подводных трубопроводов в случае, если гидродинамические силы сопротивления значительно превышают конструкционные. Величина декремента колебания δ, характеризующая суммарные силы сопротивления, может быть установлена па основании экспериментальных исследований в натурных условиях. Возможно, величина δ есть функция амплитуды колебаний.

От назначения величины суммарных сил сопротивления существенно зависят амплитуда колебания и динамические напряжения в трубопроводе. Кроме того, величина суммарных сил сопротивления позволяет установить возможность возникновения колебаний или диапазон изменения приведенной ско­рости, при котором будут происходить колебания трубопро­вода.

Для ориентировочной опенки возникновения колебаний под­водных трубопроводов можно использовать величину безраз­мерного параметра демпфирования

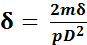(5)

где т — масса единицы длины трубопровода с учетом присое­диненной массы жидкости тпр, массы изоляции, балластировки и продукта, заполняющего трубу; р — плотность окружающей трубопровод воды.

Критическое значение δкр >, выше которого не наблюдается колебаний в направлении потока, равно 1,2. Для колебаний в поперечном к потоку направлении δкр>=17.

С увеличением δ уменьшается диапазон приведенной ско­рости v =v/nD= 1/Sh, при котором происходят колебания под­водного трубопровода. При значениях приведенной скорости v>1 иногда происходят колебания с частотой срыва вихрей, от­личающейся от частоты собственных колебаний трубопровода, а v<1,2 колебания цилиндрических конструкций не наблюдаются.