Разбиение на классы. Отношение эквивалентности
В самых различных вопросах встречается разбиение тех или иных множеств на попарно пересекающиеся подмножества. Например, плоскость (рассматриваемую как множество точек) можно разбить на прямые, параллельные оси х, жителей данного города можно разбить на группы по их году рождения и т.д.
Каждый раз, когда некоторое множество М представлено тем или иным способом как сумма попарно непересекающихся подмножеств, мы говорим о разбиении множества М на классы.
Обычно приходится иметь дело с разбиениями, построенными на базе того или иного признака, по которому элементы множества М объединяются в классы.
Пусть М – некоторое множество и пусть некоторые из пар (а, b)
элементов этого множества являются выделенными. Если (а, b) – выделенная пара, то мы будем говорить, что элемент а связан с b отношением j, и обозначать это символом аjb или(а, b) Îj. Например, если имеется в виду разбиение треугольников на классы равновеликих, то аjb означает «треугольник а имеет ту же площадь, что и треугольник b».
Определение. Отношение j называется отношением эквивалентности, если оно обладает следующими свойствами:
1) рефлексивность: аjа для любого элемента а Î М,
2) симметричность: если аjb, то bjа,
3) транзитивность: если аjb и bjc , то ajc.
Эти условия необходимы и достаточны для того, чтобы отношение j (признак!) позволяло разбить множество М на классы.
Понятие эквивалентности является частным случаем более общего понятия бинарного отношения.
Прямым (декартовым) произведением множеств А1, …, Аn называется множество А1´…´Аn = {( a1, …, an) | a1 Î А1, …, an Î Аn}.
Если А1 = … = Аn = А, то множество А1´…´Аn называется прямой степенью множества А и обозначается через Аn.
Бинарным отношением между элементами множеств А и В называется любое подмножество R множества А´В. Если А = В, то отношение R называется бинарным отношением на А. Вместо (х, у) Î R часто пишут хRу , т.е.высказывание: «предметы  и
и 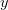 связаны бинарным отношением
связаны бинарным отношением 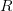 » записывают в виде
» записывают в виде 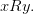 Если
Если 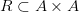 , то говорят, что бинарное отношение определено на множестве
, то говорят, что бинарное отношение определено на множестве 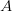 .
.
Примером бинарного отношения может служить отношение тождества e: (а, b) Î e в том и только том случае, если а = b. Иначе говоря, это – отношение, задаваемое диагональю D в М´М, т.е. подмножеством пар вида (а, а).
Областью определения бинарного отношения R называется множество dR = {x | существует у такое, что (х, у) Î R}.
Областью значений бинарного отношения R называется множество rR = {x | существует у такое, что (у, х) Î R}.
Для бинарных отношений определены обычным образом теоретико-множественные операции объединения, пересечения и т.д.
Непрерывность функции
1.1. Непрерывность функции в точке Определение. Функция у = f(x), определённая на интервале ]a, b[, называется непрерывной в точке х0 Î ]a, b[, если 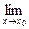 f(х) = f(х0) (то есть предел функции равен её значению при предельном значении аргумента). Так как равенство в определении равносильно следующему f(х) = f(х0) (то есть предел функции равен её значению при предельном значении аргумента). Так как равенство в определении равносильно следующему 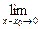 (f(х) – f(х0)) = 0, то функция непрерывна в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции. Теорема 1.1.1. Если функции f(x) и j(х) непрерывны в точке х (f(х) – f(х0)) = 0, то функция непрерывна в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции. Теорема 1.1.1. Если функции f(x) и j(х) непрерывны в точке х 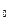 , то также непрерывны в этой точке их сумма f(x) + j(х), разность f(x) – j(х), произведение f(x)×j(х), а также частное , то также непрерывны в этой точке их сумма f(x) + j(х), разность f(x) – j(х), произведение f(x)×j(х), а также частное 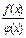 при условии, что j(х) ¹ 0. Следствие 1. Целая рациональная функция Рn(х) = a0 + a1x + a2x2 + … + anxn непрерывна при всех х. Следствие 2. Дробно рациональная функция при условии, что j(х) ¹ 0. Следствие 1. Целая рациональная функция Рn(х) = a0 + a1x + a2x2 + … + anxn непрерывна при всех х. Следствие 2. Дробно рациональная функция 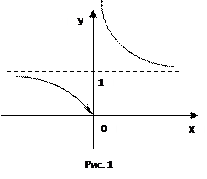 R(x) = R(x) = 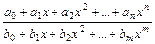 непрерывна при всех х, для которых знаменатель не обращается в нуль. Теорема 1.1.2. Если функция j(х) непрерывна в точке х0, а функция f(у) непрерывна в точке у0 = j(х0), то сложная функция F(x) = f(j(х)) непрерывна в точке х0. 1.2 Точки разрыва функции Рассмотрим функцию у = f(x), определённую на интервале ]a, b[, кроме, быть может, точки х0 Î ]a, b[. Определение. Точка х0 называется точкой разрыва данной функции, если в ней функция определена, но не является непрерывной, или не определена в этой точке. Если х0 – точка разрыва функции f(x) и существуют конечные пределы f(х0 – 0) = непрерывна при всех х, для которых знаменатель не обращается в нуль. Теорема 1.1.2. Если функция j(х) непрерывна в точке х0, а функция f(у) непрерывна в точке у0 = j(х0), то сложная функция F(x) = f(j(х)) непрерывна в точке х0. 1.2 Точки разрыва функции Рассмотрим функцию у = f(x), определённую на интервале ]a, b[, кроме, быть может, точки х0 Î ]a, b[. Определение. Точка х0 называется точкой разрыва данной функции, если в ней функция определена, но не является непрерывной, или не определена в этой точке. Если х0 – точка разрыва функции f(x) и существуют конечные пределы f(х0 – 0) = 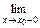 f(х), f(х0 + 0) = f(х), f(х0 + 0) = 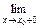 f(х), то она называется точкой разрыва первого рода. Величина f(х0 + 0) – f(х0 – 0) называется скачком функции f(x) в точке х0. Пусть функция у = f(x) имеет разрыв в точке х0 и f(х0 + 0) = f(х0 – 0), тогда х0 называется точкой устранимого разрыва. Это название оправдано тем, что если доопределить такую функцию (если она не была определена в точке х0), положив f(х0) = f(х), то она называется точкой разрыва первого рода. Величина f(х0 + 0) – f(х0 – 0) называется скачком функции f(x) в точке х0. Пусть функция у = f(x) имеет разрыв в точке х0 и f(х0 + 0) = f(х0 – 0), тогда х0 называется точкой устранимого разрыва. Это название оправдано тем, что если доопределить такую функцию (если она не была определена в точке х0), положив f(х0) = 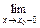 f(х) = f(х) = 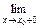 f(х), то получится функция, непрерывная в точке х0. Например, для функции f(x) = f(х), то получится функция, непрерывная в точке х0. Например, для функции f(x) = 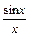 точка х0 = 0 является точкой устранимого разрыва. Если х0 – точка разрыва и, по крайней мере, один из пределов f(х0 + 0), f(х0 – 0) является бесконечным или не существует, то х0 называется точкой разрыва второго рода. Например, 1) точка х0 = 0 – точка разрыва второго рода для функции f(x) = точка х0 = 0 является точкой устранимого разрыва. Если х0 – точка разрыва и, по крайней мере, один из пределов f(х0 + 0), f(х0 – 0) является бесконечным или не существует, то х0 называется точкой разрыва второго рода. Например, 1) точка х0 = 0 – точка разрыва второго рода для функции f(x) = 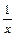 , поскольку f(х0 – 0) = –¥, f(х0 + 0) = +¥; 2) так как f(х0 + 0) = +¥, то точка х0 = 0 является точкой разрыва второго рода для функции f(x) = 3 , поскольку f(х0 – 0) = –¥, f(х0 + 0) = +¥; 2) так как f(х0 + 0) = +¥, то точка х0 = 0 является точкой разрыва второго рода для функции f(x) = 3 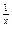 (см. рис. 1). 1.3. Непрерывность функции на промежутке Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала. (см. рис. 1). 1.3. Непрерывность функции на промежутке Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала. 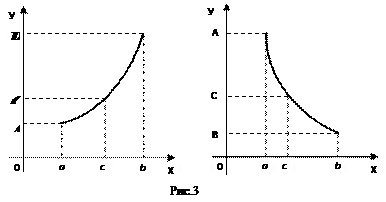 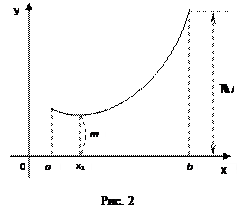 Если функция определена при х = а и при этом Если функция определена при х = а и при этом 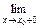 f(х) = f(а), то говорят, что f(х) в точке а непрерывна справа. Аналогично, если f(х) = f(а), то говорят, что f(х) в точке а непрерывна справа. Аналогично, если 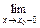 f(х) = f(b), то говорят, что в точке b эта функция непрерывна слева. Определение. Функция называется непрерывной на отрезке [a, b], если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева). Наибольшим значением функции у = f(x) на отрезке [a, b] называется такое её значение f(x1), что f(x) £ f(x1) для всех х Î [a, b]. Наименьшим значением функции у = f(x) на отрезке [a, b] называется такое её значение f(x2), что f(x) ³ f(x2) для всех х Î [a, b]. Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами. Теорема 1.3.1. Функция, непрерывная на отрезке [a, b], достигает на нём своего наименьшего значения m и наибольшего значения M, то есть существуют такие точки x1 и x2 этого отрезка, что f(x1) = m, f(x2) = M. Теорема имеет простой геометрический смысл (см. рис.2). Теорема 1.3.2. Если функция у = f(x) непрерывна на отрезке [a, b] и на его концах принимает неравные значения f(а) = А, f(b) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [a, b] такая, что f(с) = С. Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A < C < B (или A > C > B), пересекает график функции у = f(x). Следствие. Если функция непрерывна на отрезке и на его концах принимает f(х) = f(b), то говорят, что в точке b эта функция непрерывна слева. Определение. Функция называется непрерывной на отрезке [a, b], если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева). Наибольшим значением функции у = f(x) на отрезке [a, b] называется такое её значение f(x1), что f(x) £ f(x1) для всех х Î [a, b]. Наименьшим значением функции у = f(x) на отрезке [a, b] называется такое её значение f(x2), что f(x) ³ f(x2) для всех х Î [a, b]. Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами. Теорема 1.3.1. Функция, непрерывная на отрезке [a, b], достигает на нём своего наименьшего значения m и наибольшего значения M, то есть существуют такие точки x1 и x2 этого отрезка, что f(x1) = m, f(x2) = M. Теорема имеет простой геометрический смысл (см. рис.2). Теорема 1.3.2. Если функция у = f(x) непрерывна на отрезке [a, b] и на его концах принимает неравные значения f(а) = А, f(b) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [a, b] такая, что f(с) = С. Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A < C < B (или A > C > B), пересекает график функции у = f(x). Следствие. Если функция непрерывна на отрезке и на его концах принимает 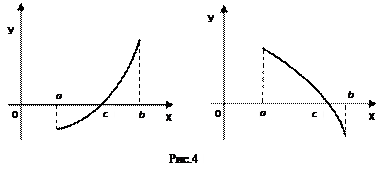 значения разных знаков, то на этом отрезке найдётся хотя бы одна точка, в которой функция обращается в нуль. Геометрический смысл следствия иллюстрируется на рис.4. Производная функции. Физический и геометрический смысл производной. Правила дифференцирования Производная функции одно из основополагающих понятий математического анализа. Мы рассмотрим основные понятия и теоремы связанные с производной функции, также обсудим геометрический и физический смысл производной функции, приведем перечень правил, которые нужно соблюдать при вычислении производной функции одной переменной и сложной функции. значения разных знаков, то на этом отрезке найдётся хотя бы одна точка, в которой функция обращается в нуль. Геометрический смысл следствия иллюстрируется на рис.4. Производная функции. Физический и геометрический смысл производной. Правила дифференцирования Производная функции одно из основополагающих понятий математического анализа. Мы рассмотрим основные понятия и теоремы связанные с производной функции, также обсудим геометрический и физический смысл производной функции, приведем перечень правил, которые нужно соблюдать при вычислении производной функции одной переменной и сложной функции. |
1. Определение производной функции.
Необходимое условие существования производной
Пусть функция 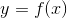 определена в точке
определена в точке 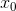 и некоторой ее окрестности. Придадим аргументу
и некоторой ее окрестности. Придадим аргументу 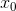 приращение
приращение 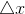 такое, что точка
такое, что точка 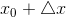 попадает в область определения функции. Функция при этом получит приращение
попадает в область определения функции. Функция при этом получит приращение 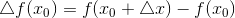 .
.
ОПРЕДЕЛЕНИЕ 1. Производной функции 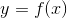 в точке
в точке 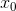 называется предел отношения приращения функции в этой точке к приращению аргумента
называется предел отношения приращения функции в этой точке к приращению аргумента 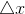 , при
, при 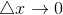 (если этот предел существует и конечен), т.е.
(если этот предел существует и конечен), т.е.
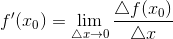 .
.
Следующая теорема устанавливает связь между существованием производной функции в точке 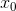 и непрерывностью функции в этой точке.
и непрерывностью функции в этой точке.
Теорема1. (необходимое условие существования производной функции в точке). Если функция y = f(x) имеет производную в точке 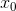 , то функция f(x) в этой точке непрерывна.
, то функция f(x) в этой точке непрерывна.
ДОКАЗАТЕЛЬСТВО
Пусть существует 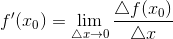 . Тогда
. Тогда
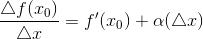 ,
,
Где 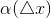 – бесконечно малая при
– бесконечно малая при 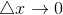 .
.
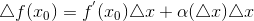 ;
;
.
Но это означает, что функция f(x) непрерывна в точке 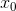 (по геометрическому определению непрерывности). ∎
(по геометрическому определению непрерывности). ∎
Замечание. Непрерывность функции в точке 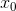 не является достаточным условием существования производной этой функции в точке
не является достаточным условием существования производной этой функции в точке 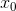 . Например, функция y = |x| непрерывна, но не имеет производной в точке
. Например, функция y = |x| непрерывна, но не имеет производной в точке 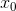 .
.
Очевидно, что соответствие 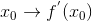 является функцией, определенной на некотором множестве
является функцией, определенной на некотором множестве 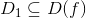 . Ее называют производной функции y = f(x) и обозначают
. Ее называют производной функции y = f(x) и обозначают
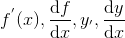 .
.
Операцию нахождения производной функции f(x) называют дифференцированием функции y = f(x).
2. Физический и геометрический смысл производной
