Вероятностное представление результатов и погрешностей измерений

Учитывая присутствие погрешности в результате измерений Х, последний можно представить в виде следующего выражения

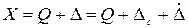, (2.4)

где 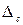- систематическая составляющая погрешности ;

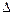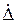- случайная составляющая погрешности .

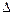Поскольку результат измерения содержит случайную погрешность и неопределенную по величине систематическую погрешность, то он сам является случайной величиной. Как и всякая случайная величина, результат измерения полностью характеризуется плотностью распределения 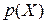. Примерный вид 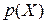изображен на рис. 2.2.

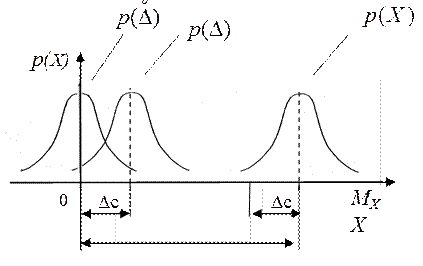
Рис. 2.2 - Вероятностное представление результатов и погрешностей измерений

На этом же рисунке изображены плотности распределения случайной погрешности 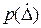и суммарной погрешности .

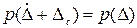Случайная погрешность по определению является центрированной случайной величиной. Поэтому ее математическое ожидание 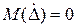. Наличие систематической погрешности приводит к смещению математического ожидания суммарной 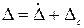погрешности на величину

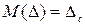. Плотность распределения результата измерения 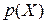смещена относительно суммарной погрешности на величину .

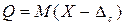Таким образом, взаимное положение истинного значения ФВ 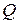и результата ее измерения Х на числовой оси не определено. Поэтому мы не можем по результату измерений определить 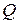, но можно попытаться оценить интервал, в который с заданной (доверительной) вероятностью попадает 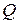. Этот интервал также называется доверительным (рис. 2.3). Термин “доверительный” выражает степень доверия к результату измерений.

Доверительным интервалом называется интервал, границы которого симметричны относительно математического ожидания, а вероятность попадания в который результата измерений, равна доверительной.

На рис. 2.3 видно, что ширина доверительного интервала 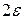зависит от доверительной вероятности Р_Δ, вида распределения и его среднеквадратического отклонения, которое характеризует степень рассеяния результатов измерений вокруг математического ожидания М_Х.

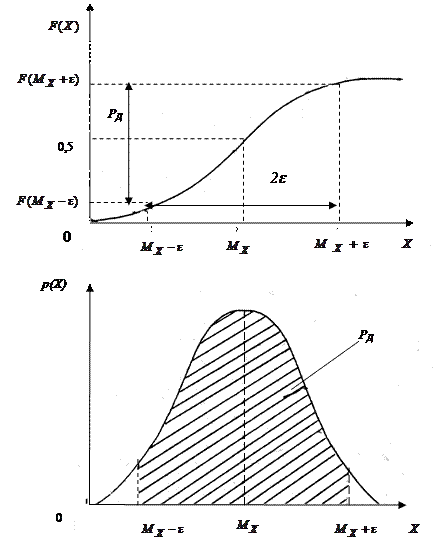Рисунок 2.3 - Доверительная вероятность и доверительный интервал

2.3 Случайные погрешности

Случайной мы называем погрешность, которая хаотично меняет свой размер и знак при повторных измерениях ФВ одного и того же размера, проводимых в одинаковых условиях.

Из этого определения вытекает способ обнаружения случайной погрешности, заключающийся в анализе результатов многократных наблюдений ФВ неизменного размера. Его удобно проводить, имея графическое изображение результатов последовательных наблюдений измеряемой величины .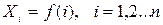

Оценивание случайной погрешности производится путем определения ее границ 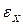, связанных с оценкой среднеквадратического отклонения (СКО) результатов наблюдений выражением

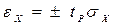, (2.29)

где 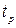- доверительный коэффициент.

Как следует из выражения (2.29) для отыскания 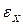необходимо:

1) произвести оценку СКО 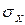, которую невозможно найти без отыскания оценки математического ожидания ;

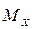2) определить закон распределения случайной погрешности для нахождения .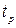

2.4 Грубые погрешности и промахи

Грубые погрешности и промахи являются особым видом случайных погрешностей. Грубые погрешности вызваны, как правило, резкими кратковременными изменениями условий измерений: механическими толчками, вибрациями, колебаниями внешних условий, скачками питающего напряжения. Промахи относятся к личным погрешностям и обусловлены неправильными действиями оператора (некорректное считывание показаний прибора, неправильной их записью и т.п.) И те, и другие погрешности вызывают заметные отличия в результатах наблюдений. Такие “подозрительные” результаты не подчиняются закону распределения основной массы результатов наблюдений и должны быть устранены из их числа.

Обнаружение грубых погрешностей и промахов производится с помощью специальных критериев, основанных на аппарате математической статистики.

2.5 Систематические погрешности

Систематические погрешности остаются постоянными или закономерно изменяются при повторных измерениях ФВ одного и того же размера.

Систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструктивных и технологических особенностей СИ, условий их применения, а также индивидуальных качеств наблюдателя.

Случайные погрешности могут быть изучены и минимизированы с помощью методов математической статистики и теории вероятности. Причины возникновения случайных погрешностей можно при этом не анализировать, повышение точности измерения достигается путем увеличения количества измерений.

Систематические погрешности остаются в результате измерения после проведения статистической обработки. Для их обнаружения и исключения необходимо провести специальный эксперимент. Эта задача требует глубокого изучения всей совокупности опытных данных измерения. Для ее решения нет готовых рекомендаций - здесь многое зависит от опыта, искусства и остроумия наблюдателя.

2.5.1 Классификация систематических погрешностей

По месту (причине) возникновения систематические погрешности делятся на методические, инструментальные и личные.

К методическим погрешностям (погрешностям метода измерения) относят следующие погрешности.

1. Погрешности, возникающие из-за несоответствия объекта измерения его модели. Например, погрешность измерения диаметра вала, сечение которого отличается от идеальной окружности; погрешность измерения среднеквадратического значения напряжения переменного тока, если его форма отлична от синусоидальной.

2. Погрешности, возникающие из-за воздействия средства измерения на объект. Например, погрешности измерения напряжения на резисторе вольтметром, имеющим малое собственное сопротивление, погрешности измерения распределения электромагнитного поля с помощью антенны конечных размеров, погрешности измерения температуры тела, возникающие из-за оттока тепла через датчик температуры и т.д.

3. Погрешности, заложенные в принцип действия средства измерения при его разработке. Например, погрешности квантования при аналого-цифровом преобразовании (несовершенство отражения непрерывного по размеру значения ФВ дискретным числом).

4. Погрешности косвенных измерений, обусловленные упрощением связи между измеряемой величиной и ее аргументами, измеряемыми с помощью прямых измерений. Например, измерение количества жидкости по ее уровню в сосуде, В общем случае это нелинейная функция, которую принимают за линейную.

5. Погрешности, обусловленные несовершенством алгоритма вычисления результата измерения, например, погрешность определения математического ожидания через среднее арифметическое, погрешности численных методов, например, численного интегрирования и дифференцирования, вычисление функции путем разложения ее в ряд и т.п.

Инструментальные погрешности - это погрешности, обусловленные несовершенством СИТ.

1. Погрешности, обусловленные ограниченностью диапазона действия физических явлений, положенных в основу принципа действия измерительного прибора. Эти погрешности, в зависимости от режима использования СИТ разделяют на статические и динамические. Примером статической погрешности является погрешность, обусловленная нелинейностью амплитудной характеристики СИТ, например, нелинейность закона Гука в широком диапазоне, нелинейность температурных датчиков (эффект Зеебека) при измерении температуры, частотные погрешности. Примером динамических погрешностей являются погрешности, обусловленные инерционными свойствами СИТ (инерционностью термометра при измерении температуры, инерционными свойствами спидометра при определении быстроменяющихся скоростей и т.д.),

2. Погрешности, обусловленные недостатком технологии изготовления или конструкции СИТ. Например, неравенство плеч у весов, неудовлетворительная подгонка мер, эксцентричность вращающихся частей измерительных приборов, люфт микрометрических винтов и т.д.

3. Погрешности, обусловленные неточностью выполнения метрологических операций с СИТ (градуировки, калибровки, поверки).

4. Погрешности от неправильной эксплуатации СИТ (неправильной установки или юстировки СИТ, расположения СИТ в сильных электрических или магнитных полях, помех в питающей сети от электрических машин и механизмов, влияния СИТ друг на друга).

Личные погрешности, или погрешности оператора обусловлены следующими факторами.

1. Инерционными свойствами органов чувств наблюдателя, например, при запаздывании в отсчетах времени максимального положения маятника.

2. Влиянием месторасположения наблюдателя и особенности системы отсчета (параллакс), ошибки в интерполяции отсчета, попадающего между двумя оцифрованными отметками и др.

3. Ограничением диапазона чувствительности и нелинейностью характеристик восприятия органов чувств, например, неправильное определение нулевых биений при измерении частоты гетеродинным частотомером обусловлено ограничением снизу частотного диапазона чувствительности уха.

В зависимости от характера изменения систематические погрешности подразделяются на постоянные и переменные (монотонные и периодические).

Пример постоянной систематической погрешности - погрешность гири, имеющей массу 1,001 кг. Все измерения, выполняемые с применением этой гири, будут сопровождаться постоянной погрешностью 0,001 кг. Другой пример – погрешность, обусловленная неравенством плеч моста постоянного тока или разноплечестью весов. В этом случае возникает постоянная относительная погрешность измерения сопротивления или массы взвешиваемого груза.

Монотонные (прогрессивные погрешности) – те, которые возрастают или убывают во времени. Пример - погрешность измерения напряжения с помощью потенциометра, обусловленная падением напряжения нормального элемента в его цепи или аналогичная погрешность измерения сопротивления резистора (методом амперметра), обусловленная разрядом питающих элементов.

Периодические погрешности периодически изменяют свою величину и знак. Например, погрешность, обусловленная смещением оси у секундомера относительно центра шкалы.

Систематическая погрешность может не зависеть или зависеть от значения измеряемой величины и соответственно быть аддитивной или мультипликативной.

2.5.2 Обнаружение систематических погрешностей

Бели результат наблюдения X содержит систематическую погрешность 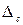, то оценка математического ожидания результата наблюдения

.

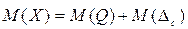В отличие от случайных погрешностей 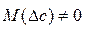. Поэтому обнаружение и минимизация систематических погрешностей таким же образом, как и случайных не представляются возможными.

Способы обнаружения систематической погрешности различаются в зависимости от характера ее изменения.

Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от среднего арифметического, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основе априорных знаний об этих погрешностях, получаемых, например, при поверке СИТ, которая может осуществляться двумя способами.

1. С помощью эталонной меры. Измеряемая величина при поверке воспроизводится эталонной мерой, значение которой известно. Поэтому разность между средним арифметическим результата наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения равна искомой систематической погрешности. Ценность полученных при поверке результатов определяется их постоянством в течение некоторого промежутка времени (межповерочного интервала) и их независимостью от внешних условий. Если СИТ имеет возможность измерять нулевое значение ФВ, то последнее (при аддитивной абсолютной погрешности СИТ) можно использовать вместо эталонной меры. Показания СИТ при отсутствии измеряемой величины будут равны искомой систематический погрешности.

2. С помощью эталонного СИТ. Произвольная по значению ФВ одновременно измеряется с помощью исследуемого СИТ и более точного (эталонного). Разность между их результатами измерения с погрешностью эталонного СИТ равна систематической погрешности исследуемого СИТ.

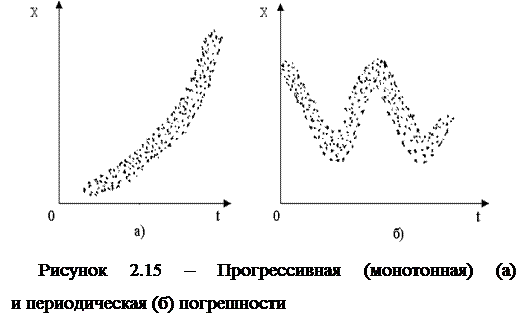
Переменные систематические погрешности, существенные по сравнению со случайными погрешностями, можно обнаружить, построив график последовательности результатов наблюдений или их отклонений от среднего арифметического. При прогрессивной систематической погрешности последовательность результатов наблюдений обнаруживает тенденцию к возрастанию или убыванию (рис.2.15, а), а при наличии периодической систематической погрешности прослеживаются колебания средних значений случайных отклонений (рис.2.15, б).

Если систематическая переменная погрешность соизмерима со случайной, то ее можно обнаружить с помощью специальных методов обработки. В этом случае можно воспользоваться аппаратом дисперсионного анализа. Дисперсионный анализ основан на исследованиях закономерностей соотношения дисперсий и средних арифметических разных групп наблюдений.