Замечательных пределов
1. Понятие неопределенности. В практике отыскания пределов наиболее часто применяется теорема 2 об арифметических действиях над пределами (см. § 1). Однако ее непосредственное применение бывает невозможно в особых ситуациях, называемых неопределенностями, которые возникают при нарушении ее условий. Например, если 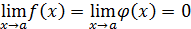 , то нельзя сказать ничего определенного о пределе
, то нельзя сказать ничего определенного о пределе 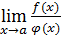 , не зная конкретного вида функции
, не зная конкретного вида функции 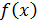 и
и 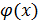 . В этом случае говорят о наличии неопределенного вида
. В этом случае говорят о наличии неопределенного вида  . Неопределенность возникает и при отыскании предела
. Неопределенность возникает и при отыскании предела 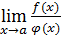 , если
, если 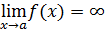 ,
, 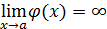 (
( 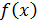 и
и 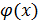 могут быть бесконечно большими определенного знака или нет). Ее обозначают символом
могут быть бесконечно большими определенного знака или нет). Ее обозначают символом 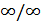 . Еще один пример: ищется
. Еще один пример: ищется 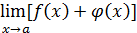 , причем
, причем 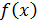 и
и 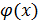 – бесконечно большие противоположных знаков – здесь неопределенность
– бесконечно большие противоположных знаков – здесь неопределенность 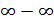 . При вычислении предела
. При вычислении предела 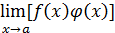 создается неопределенность
создается неопределенность 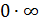 , если
, если 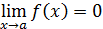 ,
, 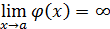 . Кроме этих неопределенностей, связанных с арифметическими действиями над пределами, существуют неопределенности
. Кроме этих неопределенностей, связанных с арифметическими действиями над пределами, существуют неопределенности 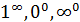 , относящиеся к пределу вида
, относящиеся к пределу вида 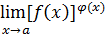 .
.
Чтобы найти пределы при наличии неопределенности, надо эту неопределенность устранить, открыв тем самым возможность использования тех или иных теорем о пределах. Это достигается, с одной стороны, применением алгебраических и тригонометрических преобразований (разложение функций на множители или на слагаемые, приведение дробей к общему знаменателю, добавление и вычитание некоторого выражения, умножение и деление на некоторую функцию, вынесение множителя за скобку и т.п.), заменой переменной, использованием эквивалентных бесконечно малых и бесконечно больших (см. § 3), а с другой стороны, использованием так называемых замечательных пределов.
I. 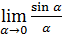 .
.
II. 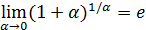 (
( 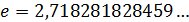 — иррациональное число. Оно является основанием системы логарифмов, называемых натуральными. Вместо
— иррациональное число. Оно является основанием системы логарифмов, называемых натуральными. Вместо 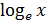 принято писать
принято писать 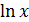 ).
).
Из предела II выводятся следующие пределы, широко применяемые при раскрытии неопределенностей:
III. 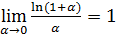 .
.
IV. 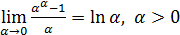 (в частности,
(в частности, 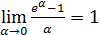 ).
).
V. 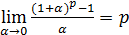 .
.
Замечание. Применение замечательных пределов требует понимания и запоминания структуры каждого из них и при этом необходимости ее воспроизведения. Так, для предела 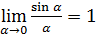 характерно отношение синуса бесконечно малого угла к самому углу. Поэтому всякий предел вида
характерно отношение синуса бесконечно малого угла к самому углу. Поэтому всякий предел вида 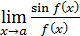 равен 1, если
равен 1, если 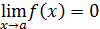 . Например, каждый из пределов
. Например, каждый из пределов 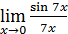 ,
, 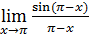 ,
, 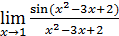 есть, в сущности, первый замечательный предел и потому равен 1, чего нельзя сказать ни об одном из пределов
есть, в сущности, первый замечательный предел и потому равен 1, чего нельзя сказать ни об одном из пределов 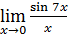 ,
, 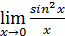 ,
, 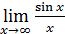 .
.
Для предела 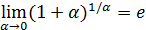 характерно, что сумма, равная единице плюс бесконечно малая, возводится в степень, обратную этой бесконечно малой. Следовательно, если
характерно, что сумма, равная единице плюс бесконечно малая, возводится в степень, обратную этой бесконечно малой. Следовательно, если 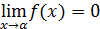 , то и
, то и 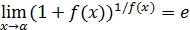 . Такова структура каждого из пределов
. Такова структура каждого из пределов 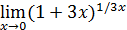 ,
, 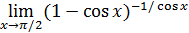 ,
, 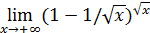 , и потому все они равны
, и потому все они равны 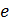 , но структура пределов
, но структура пределов 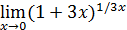 ,
, 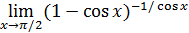 ,
, 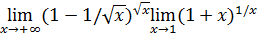 отлична от срукткры замечательного предела.
отлична от срукткры замечательного предела.
Подобные рассуждения справедливы и для пределов III–V.
Заметим, что если заданный предел не обладает структурой ни одного из пределов I–V, это не исключает возможности использования их для его отыскания.
2. Неопределенность 0/0. В простейших случаях такая неопределенность устраняется путем выделения в числителе и знаменателе общего множителя, создающего неопределенность, и сокращения на него, после чего можно применять теорему о пределе частного. Этот прием основан на теореме: если в окрестности точки 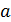
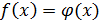 для всех
для всех 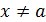 и существует один из пределов
и существует один из пределов 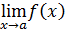 или
или 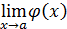 , то существует и другой, и они равны. Например, функции
, то существует и другой, и они равны. Например, функции 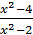 и
и 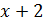 равны при
равны при 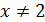 . Поскольку
. Поскольку 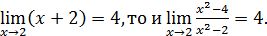
Способ выделения общего множителя, да и сам его вид зависят от структуры числителя и знаменателя. Иногда вид выделяемого множителя зависит от способа его выделения (см. ниже пример 5). Для раскрытия неопределенности 0/0 применяются и другие элементарные приемы, а также пределы I, III–V, используются эквивалентные бесконечно малые.
Пример 1. Вычислить 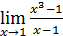 .
.
Решение. Многочлены, стоящие в числителе и знаменателе, обращаются в нуль при 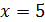 . По теореме Безу каждый из них должен делиться на
. По теореме Безу каждый из них должен делиться на 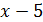 , т.е. каждый из них может быть представлен в виде произведения
, т.е. каждый из них может быть представлен в виде произведения 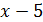 на некоторый многочлен.
на некоторый многочлен.
Таким образом, нахождение предела сводится прежде всего к выделению в числителе и знаменателе множителя 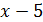 , незримое присутствие которого и создает неопределенность 0/0. Практически это достигается каким-либо способом разложения числителя и знаменателя на множители, например делением «уголком»*.
, незримое присутствие которого и создает неопределенность 0/0. Практически это достигается каким-либо способом разложения числителя и знаменателя на множители, например делением «уголком»*.
[ДЕЛЕНИЕ СТОЛБИКОМ]
Теперь искомый предел можно представить в виде
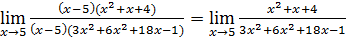 .
.
Неопределенность исчезла. По теореме о пределе частного находим ответ: 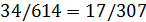 .
.
Замечание. Веденный пример решения всегда приводит к цели, когда ищется 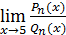 , где
, где 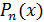 и
и 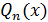 — многочлены степеней m и n относительно x. Можно применить и непосредственное разложение многочленов на множители путем группировки слагаемых с выделением множителя
— многочлены степеней m и n относительно x. Можно применить и непосредственное разложение многочленов на множители путем группировки слагаемых с выделением множителя 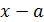 , если такая группировка очевидна. В приведенном примере такое разложение легко получить для числителя:
, если такая группировка очевидна. В приведенном примере такое разложение легко получить для числителя:
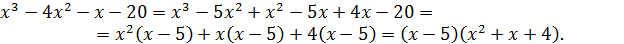
1. Раскрыть неопределенность 0/0:
1) 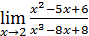 ; 3) ; 3) 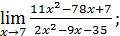 5) 5) 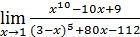 ; 7) ; 7) 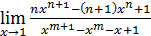 (m и n – натуральные числа); 9) (m и n – натуральные числа); 9) 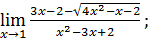 11) 11) 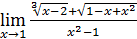 ; 13) ; 13) 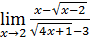 ; 15) ; 15) 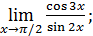 17) 17) 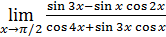 ; 19) ; 19) 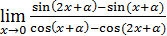 ( ( 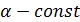 ); 21) ); 21) 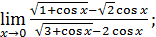 23) 23) 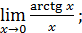 25) 25) 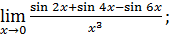 27) 27) 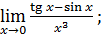 29) 29) 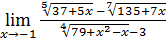 ; 31) ; 31) 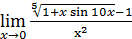 ; 33) ; 33) 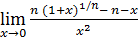 (n – натуральное число); 35) (n – натуральное число); 35) 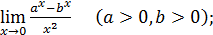 37) 37) 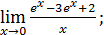 39) 39) 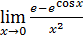 ; 41) ; 41) 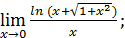 43) 43) 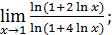 45) 45) 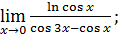 47) 47) 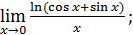 | 2) 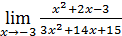 ; 4) ; 4) 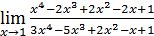 ; 6) ; 6) 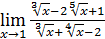 ; 8) ; 8) 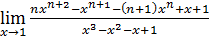 (n – натуральное число); 10) (n – натуральное число); 10) 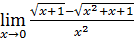 ; 12) ; 12) 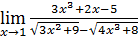 ; 14) ; 14) 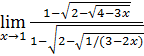 ; 16) ; 16) 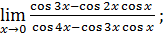 18) 18) 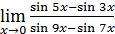 ; 20) ; 20) 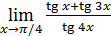 ; 22) ; 22) 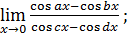 24) 24) 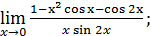 26) 26) 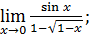 28) 28) 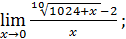 30) 30) 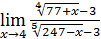 ; 32) ; 32) 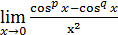 ; 34) ; 34) 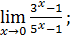 36) 36) 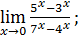 38) 38) 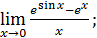 40) 40) 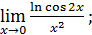 42) 42) 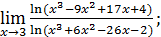 44) 44) 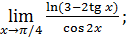 46) 46) 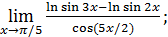 48) 48) 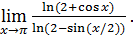 |
3. Неопределенность ∞/∞. Эта неопределенность раскрывается теми же методами, что и неопределенность 0/0, а иногда просто сводится к последней элементарными преобразованиями.
Пример 3. Вычислить 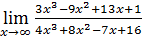 .
.
Решение. При достаточно больших значениях 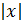 величина числителя определяется членом
величина числителя определяется членом 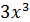 , а роль остальных слагаемых тем незначительней, чем больше
, а роль остальных слагаемых тем незначительней, чем больше 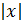 . В знаменателе при росте
. В знаменателе при росте 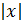 доминирующее значение приобретает слагаемое
доминирующее значение приобретает слагаемое 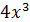 . Поэтому именно присутствие членов, содержащих
. Поэтому именно присутствие членов, содержащих 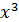 , является причиной возникновения неопределенности ∞/∞. Если в числителе и знаменателе вынести множитель
, является причиной возникновения неопределенности ∞/∞. Если в числителе и знаменателе вынести множитель 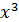 за скобки и сократить на него, то неопределенность исчезнет:
за скобки и сократить на него, то неопределенность исчезнет:
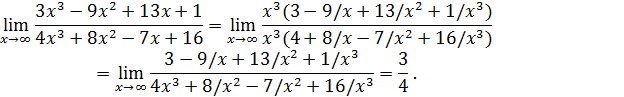
(Слагаемые 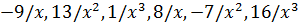 есть бесконечно малые при
есть бесконечно малые при  ).
).
Замечание. Проведенные преобразования фактически сводятся к делению числителя и знаменателя на старшую степень x. Часто этого бывает достаточно для раскрытия неопределенности ∞/∞. (В сущности, к этому же премк можно отнести замену переменной 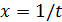 . Тогда
. Тогда 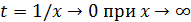 и
и
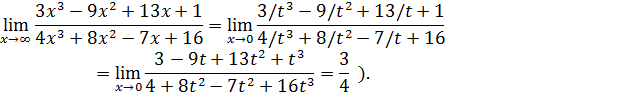
Пример 4. Вычислить 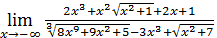 .
.
Решение. Воспользуемся замечанием к примеру 15. Заметив, что старшая степень 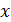 в данном случае равна 3, разделим почленно ислитель и знаменатель на
в данном случае равна 3, разделим почленно ислитель и знаменатель на 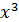 :
:
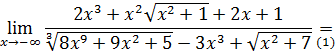
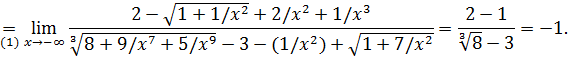
(Смена знака перед двумя радикалами в переходе (1) объясняется тем, что при 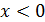
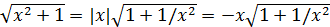 и аналогично
и аналогично 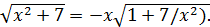
Пример 5. Вычислить 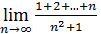 .
.
Решение. В числителе стоит сумма членов арифметической прогрессии. Следовательно, 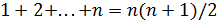 и
и
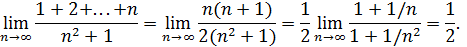
Пример 6. Вычислить 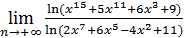 .
.
Решение. Множителем, создающим неопределенность, в данном примере является 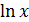 , что видно из равенств
, что видно из равенств
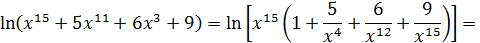
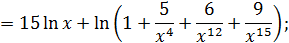
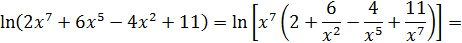
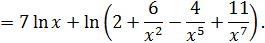
Заменив числитель и знаменатель правыми частями этих равенств и поделив их затем на 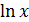 , добьемся исчезновения неопределенности:
, добьемся исчезновения неопределенности:
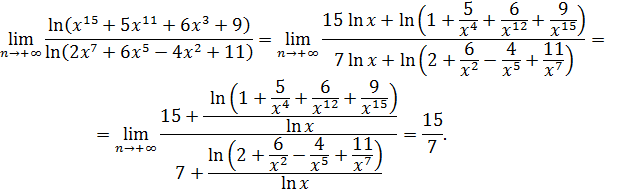
2. Раскрыть неопределенность ∞/∞:
| 49) | 1) 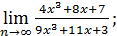 | 2) 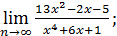 | 3) 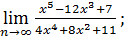 |
Вывести простое правило вычисления предела 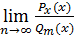 , где
, где 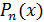 и
и 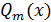 – многочлены степеней n и m.
– многочлены степеней n и m.
50) 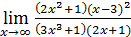 ; 52) ; 52) 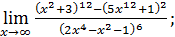 54) 54) 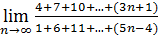 ; 56) ; 56) 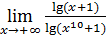 ; 58) ; 58) 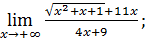 60) 60) 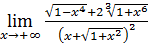 ; 62) ; 62) 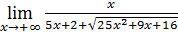 ; 64) ; 64) 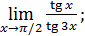 66) 66) 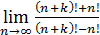 ; 68) ; 68) 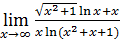 ; 70) ; 70) 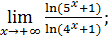 | 51) 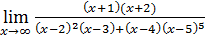 ; 53) ; 53) 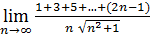 ; 55) ; 55) 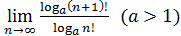 ; 57) ; 57) 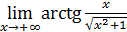 ; 59) ; 59) 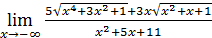 ; 61) ; 61) 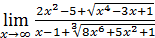 ; 63) ; 63) 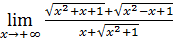 ; 65) ; 65) 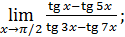 67) 67) 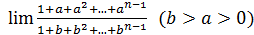 ; 69) ; 69) 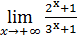 ; 71) ; 71) 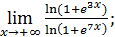 |
4. Неопределенность 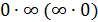 . Неопределенности такого вида элементарными преобразованиями, использованием замечательных пределов или заменой переменной сводятся к одной из неопределенностей вида 0/0 или ∞/∞.
. Неопределенности такого вида элементарными преобразованиями, использованием замечательных пределов или заменой переменной сводятся к одной из неопределенностей вида 0/0 или ∞/∞.
Пример 7. Вычислить 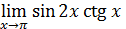 .
.
Решение.
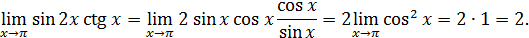
Пример 8. Вычислить 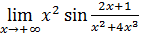 .
.
Решение. Заметив, что при 
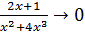 , выделим замечательны предел I:
, выделим замечательны предел I:
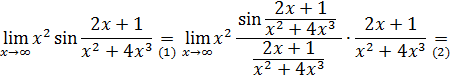
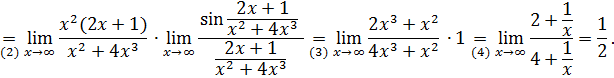
После выделения замечательного предела I делением и умножением на 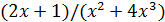 (переходы (1) – (3)) неопределенность
(переходы (1) – (3)) неопределенность 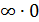 свелась к неопределенности
свелась к неопределенности 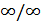 , ликвидация которой произведена делением числителя и знаменателя на старшую степень переменной (переход (4)).
, ликвидация которой произведена делением числителя и знаменателя на старшую степень переменной (переход (4)).
Вычислить следующие пределы:
72) 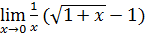 ; 74) ; 74) 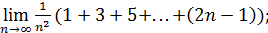 76) 76) 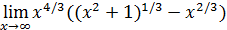 ; 78) ; 78) 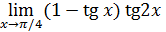 ; 80) ; 80) 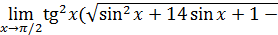 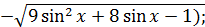 82) 82) 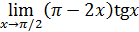 ; 84) ; 84) 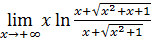 ; 86) ; 86) 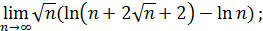 88) 88) 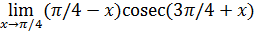 ; ; | 73) 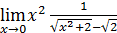 ; 75) ; 75) 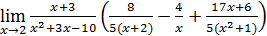 ; 77) ; 77) 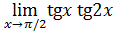 ; 79) ; 79) 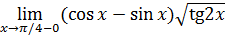 ; 81) ; 81) 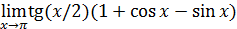 ; 83) ; 83) 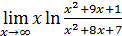 ; 85) ; 85) 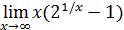 ; 87) ; 87) 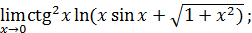 |
5. Неопределенность 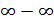 . Раскрытие этой неопределенности, нередко сопряженное с большими трудностями, достигается использованием замечательных пределов или сведением к одной из неопределенностей 0/0, ∞/∞,
. Раскрытие этой неопределенности, нередко сопряженное с большими трудностями, достигается использованием замечательных пределов или сведением к одной из неопределенностей 0/0, ∞/∞, 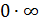 с помощью элементарных преобразований.
с помощью элементарных преобразований.
Пример 9. Вычислить 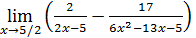 .
.
Решение. Приведение дробей к общему знаменателю сменяет неопределенность 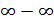 на неопределенность 0/0, которая раскрывается сокращением дроби на множитель
на неопределенность 0/0, которая раскрывается сокращением дроби на множитель 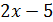 . Действительно, учитывая, что
. Действительно, учитывая, что 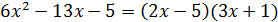 , находим последовательно
, находим последовательно
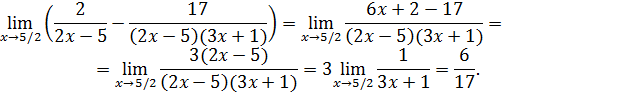
∞/∞, 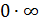 с помощью элементарных преобразований.
с помощью элементарных преобразований.
Пример 10. Вычислить 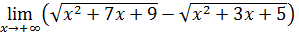 .
.
Решение. Умножение и деление на одно и то же выражение, сопряженное данному двучлену, сводит неопределенность 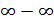 к неопределенности
к неопределенности 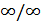 :
:
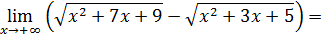
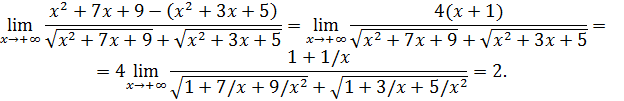
89) 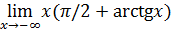 ; 91) ; 91) 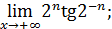 | 90) 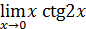 ; 92) ; 92) 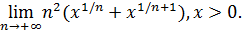 |
5. Неопределенность 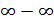 . Раскрытие этой неопределенности, нередко сопряженное с большими трудностями, достигается использованием замечательных пределов или сведением к одной из неопределенностей 0/0, ∞/∞,
. Раскрытие этой неопределенности, нередко сопряженное с большими трудностями, достигается использованием замечательных пределов или сведением к одной из неопределенностей 0/0, ∞/∞, 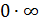 с помощью элементарных преобразований.
с помощью элементарных преобразований.
Пример 11. Вычислить 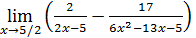 .
.
Решение. Приведение дробей к общему знаменателю сменяет неопределенность 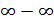 на неопределенность 0/0, которая раскрывается сокращением дроби на множитель
на неопределенность 0/0, которая раскрывается сокращением дроби на множитель 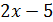 . Действительно, учитывая, что
. Действительно, учитывая, что 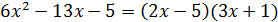 , находим последовательно
, находим последовательно
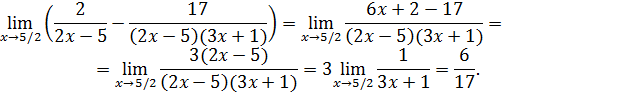
∞/∞, 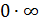 с помощью элементарных преобразований.
с помощью элементарных преобразований.
Пример 12. Вычислить 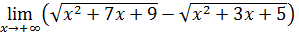 .
.
Решение. Умножение и деление на одно и то же выражение, сопряженное данному двучлену, сводит неопределенность 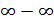 к неопределенности
к неопределенности 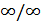 :
:
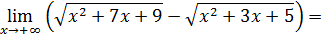
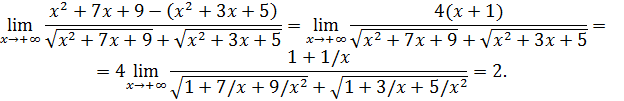
Вычислить следующие пределы:
93) 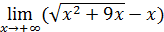 ; ; | 94) 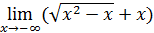 ; ; |
95) 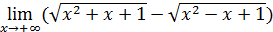 ; ; | 96) 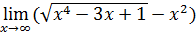 ; ; |
97) 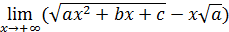 ; ; | 98) 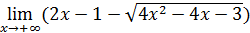 ; ; |
99) 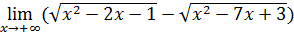 ; ; | |
100) 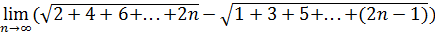 ; ; | |
101) 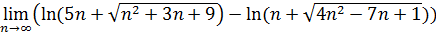 ; ; | |
102) 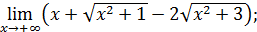 | |
103) 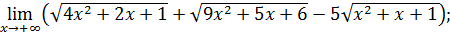 | |
104) 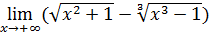 ; ; | 105) 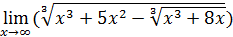 ; ; |
106) 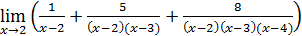 ; ; | |
107) 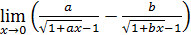 ; ; | 108) 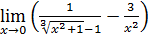 ; ; |
109) 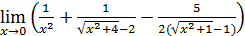 ; ; | 110) 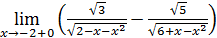 ; ; |
111) 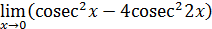 ; ; | 112) 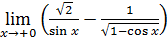 ; ; |
113) 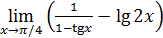 ; ; | 114) 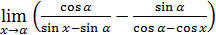 ; ; |
115) 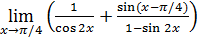 ; ; | 116) 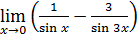 ; ; |
117) 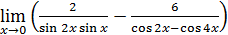 ; ; | 118) 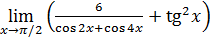 ; ; |
119) 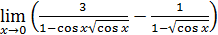 ; ; | 120) 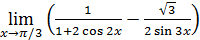 ; ; |
6. Неопределенность 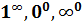 . Условия, при которых возникают эти неопределенности, связанные с пределом
. Условия, при которых возникают эти неопределенности, связанные с пределом 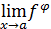 , где
, где 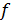 и
и 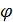 — функции от x, можно пояснить таблицей:
— функции от x, можно пояснить таблицей:
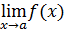 | 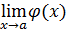 | 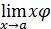 |
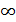 | 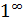 | |
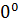 | ||
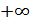 | 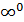 |
Из тождества 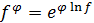 и непрерывности показательной функции (см. главу III) следует, что
и непрерывности показательной функции (см. главу III) следует, что 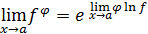 . Таким образом, раскрытие неопределенностей
. Таким образом, раскрытие неопределенностей 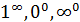 сводится к отысканию предела функции
сводится к отысканию предела функции 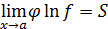 , который связан с неопределенностью
, который связан с неопределенностью 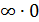 , как это видно из таблицы. Если S найдено, то
, как это видно из таблицы. Если S найдено, то 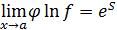 . Заметим, что
. Заметим, что 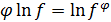 . Следовательно, для раскрытия любой из неопределенностей рассматриваемых типов достаточно найти предел натурального логарифма функции, стоящей под знаком предела, и по его значению S восстановить искомый предел
. Следовательно, для раскрытия любой из неопределенностей рассматриваемых типов достаточно найти предел натурального логарифма функции, стоящей под знаком предела, и по его значению S восстановить искомый предел 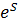 . Неопределенность
. Неопределенность 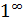 может быть раскрыта помимо изложенного способа, общего для этих неопределенностей, способом непосредственной «подгонки» к замечательному пределу II
может быть раскрыта помимо изложенного способа, общего для этих неопределенностей, способом непосредственной «подгонки» к замечательному пределу II 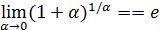 , например, по такой схеме:
, например, по такой схеме:
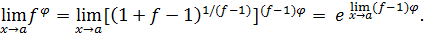
Выражение, построенное внутри квадратных скобок, имеет вид 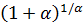 , где
, где 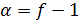 — бесконечно малая при
— бесконечно малая при 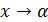 . Нахождение предела
. Нахождение предела
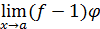 требует раскрытия неопределенности
требует раскрытия неопределенности 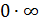 .
.
Пример 13. Вычислить 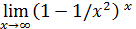 .
.
Решение. Поскольку 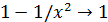 при
при  , то имеем неопределенность вида
, то имеем неопределенность вида 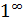 . Выделим замечательный предел II:
. Выделим замечательный предел II:
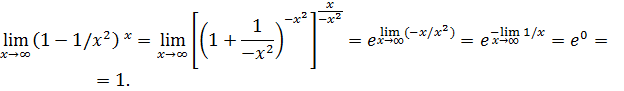
Пример 14. Вычислить 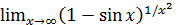 .
.
Решение. 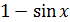 при
при 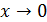 стремится к единице, а
стремится к единице, а 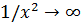 , следовательно, здесь неопределенность вида
, следовательно, здесь неопределенность вида 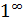 . Выделим замечательный предел II:
. Выделим замечательный предел II:
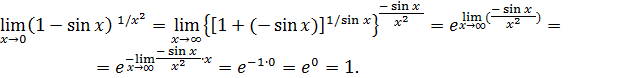
Пример 15. Вычислить 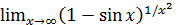 .
.
Решение. 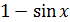 при
при 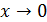 стремится к единице, а
стремится к единице, а 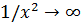 , следовательно, здесь неопределенность вида
, следовательно, здесь неопределенность вида 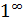 . Выделим замечательный предел II:
. Выделим замечательный предел II:
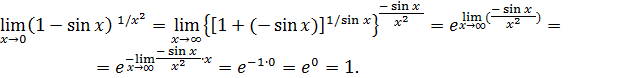
Пример 16. Вычислить 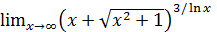 .
.
Решение. 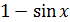 при
при 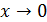 стремится к единице, а
стремится к единице, а 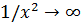 , следовательно, здесь неопределенность вида
, следовательно, здесь неопределенность вида 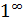 . Выделим замечательный предел II:
. Выделим замечательный предел II:
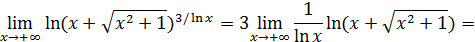
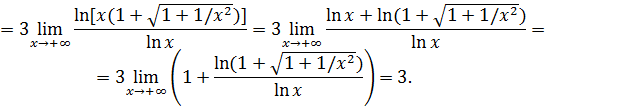
Следовательно, 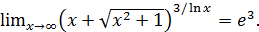
Вычислить:
121) 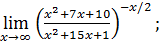 | 122) 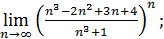 |
123) 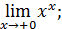 | 124) 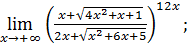 |
125) 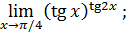 | 126) 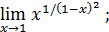 |
127) 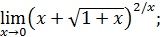 | 128) 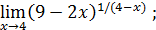 |
129) 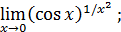 | 130) 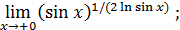 |
131) 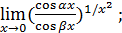 | 132) 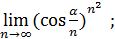 |
133) 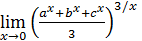 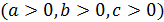 ; ; | 134) 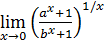 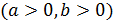 ; ; |
135) 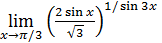 | 136) 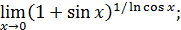 |
137) 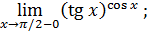 | 138) 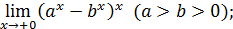 |
139) 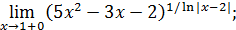 | 140) 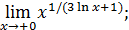 |
141) 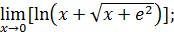 | 142) 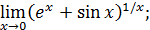 |
143) 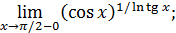 | 144) 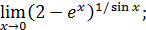 |
145) 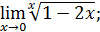 |
