Диагонализация квадратной матрицы
Рассмотрим случай неособенной модальной матрицы М, так что существует обратная матрица М-1 (это соответствует случаю различных характеристических чисел λi или случаю симметрической матрицыА), при этом решение уравнения
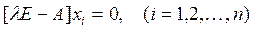
можно записать в следующем виде:
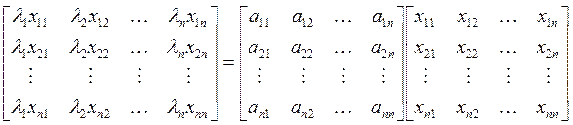
или
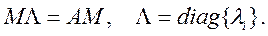
Чтобы получить диагональную матрицу Λ, необходимо получить матрицу M-1AM , т.е. осуществить преобразование:
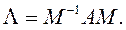
Более высокие степени А приводятся к диагональному виду таким же способом. Например,
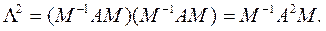
Преобразование вида B = Q-1AQ, где А и B – квадратные матрицы, а Q – неособенная квадратная матрица, называется коллинеарным преобразованием, или преобразованием подобия.
Итак, предполагая, что характеристические числа А различные, применим преобразование подобия Λ=М-1АМ, используя модальную матрицу М, к уравнениям состояния и наблюдения линейной стационарной системы в стандартной форме (см. п. 2.4, соответствующая структурная схема приведена на рис. 2.10):
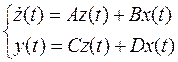
Введя линейное преобразование z = Mq, где М – модальная матрица, подставим его в эти уравнения и получим:
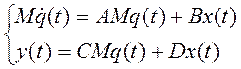 .
.
Умножение первого уравнения слева на матрицу М-1, обратную модальной, дает:
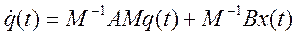 .
.
Поскольку М – модальная матрица, то преобразование подобия
М-1АМ приводит к диагональной матрице Λ. Главными диагональными элементами Λ служат характеристические числа λ1, λ2 ,…,λn. Следовательно,
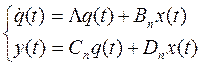 ,
,
где Λ = М-1АМ, Bn = M-1B, Cn = CM и Dn = D.
Эта форма записи уравнений известна как нормальная формауравнений состояния. При этом дифференциальные уравнения развязаны относительно переменных состояния q1, q2,…, qn, т.е. они имеют вид:
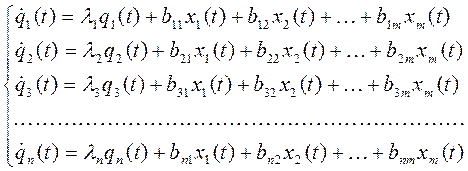
Пример. Записать уравнения состояния в нормальной форме для динамической системы, структурная схема которой приведена на рис. 2.12.
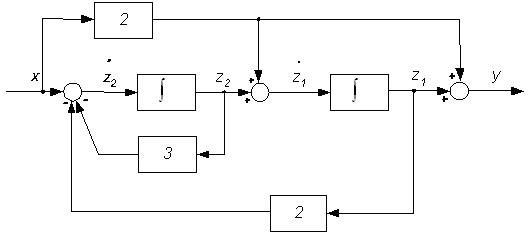
Рис. 2.12. Блок-схема стандартной формы уравнений динамической системы из примера
Соответствующая рисунку 2.12 стандартная форма уравнений состояния имеет вид:
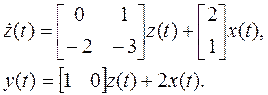
Модальные матрицы М и М-1, соответствующие матрице А, а также диагональная матрица Λ = М-1АМ, и прочие B n= M-1B, Cn = CM и Dn = D равны:
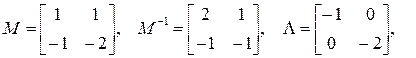
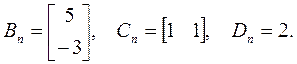
Нормальная форма уравнений состояния имеет вид:
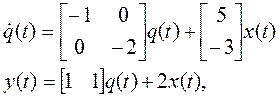
где q(t) =М-1z(t) или q1 = 2z1+z2 , q2 = – z1 – z2. Блок-схема этих уравнений показана на рис. 2.13.
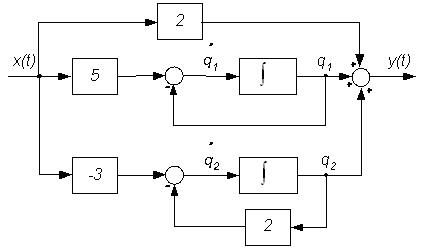
Рис. 2.13. Блок-схема нормальной формы уравнений динамической системы из примера
Вопросы к разделу 2.6
- Что такое линейная оболочка?
- Что называется базисом линейного векторного пространства?
- Какой вектор называется характеристическим?
- Каков алгоритм получения характеристического уравнения для матрицы А?
- Что называется следом матрицы?
- Что позволяет определить формула Бохера?
- Почему формула Бохера называется рекуррентной?
- Что представляют собой столбцы модальной матрицы?
- Из какой матрицы и как выбираются столбцы модальной матрицы при различных характеристических числах?
- Что образуют столбцы модальной матрицы в векторном пространстве?
- В каком случае модальная матрица не является особенной?
- При каком условии можно диагонализировать матрицу А?
- Какое преобразование называется коллинеарным?
- Что является отличительной чертой нормальной формы уравнений состояния системы?
