Синтез наблюдателя состояния по результатам измерений на основе решения ЛМН
Во многих случаях оказываются доступными для измерения не все, а только часть координат состояния или их комбинация. Для того чтобы иметь возможность реализовать на практике синтезированный закон управления в виде обратной связи по состоянию, требуется построить наблюдатель, вектор состояния которого будет давать оценку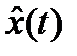 
вектора состояния x(t) в моменты времени t. При этом управление берется в виде обратной связи по состоянию наблюдателя, т.е. 
.
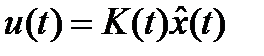Рассматривается система (1.4) с неопределенными возмущениями и неполной информацией о векторе состояния, т.е. измеряются только компоненты вектора выхода
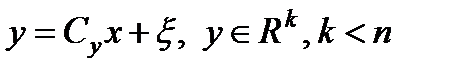, (2.1)
где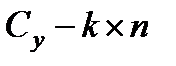 
- матрица, в общем случае зависящая от времени, 
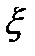- вектор погрешностей измерений, для которого имеет место ограничений
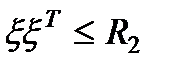, (2.2)
где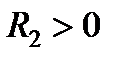 
- заданная положительно определенная 
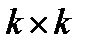матрица.
Для неопределенных возмущений имеет место ограничение (1.5).
Для рассматриваемой системы требуется синтезировать наблюдатель вектора состояния по результатам измерений в виде (аналога фильтра Калмана для детерминированной системы с неопределенными возмущениями)
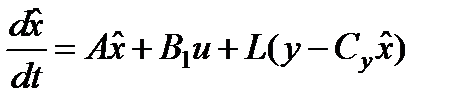, (2.3)
где матрица L коэффициентов усиления наблюдателя выбирается из условия обеспечения сходимости наблюдателя и минимума предельного множества эллипсоидальной оценки для ошибки оценивания
.
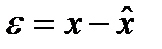Выпишем уравнение для ошибки
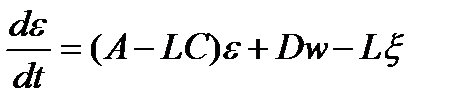(2.4)
Построим для (2.4) систему сравнения в виде
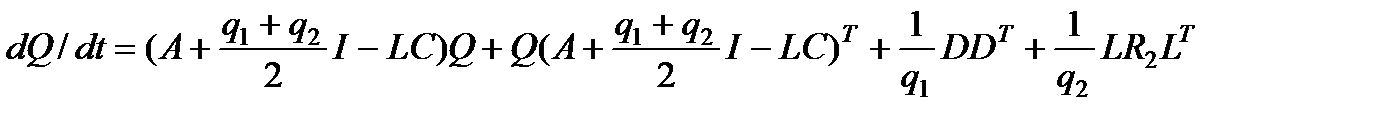. (2.5)
В случае автономной системы (когда матрицы не зависят от времени) имеет место следующая теорема.
Теорема 2.1. Предположим, что матрица A–LC в (2.5) гурвицева, т.е.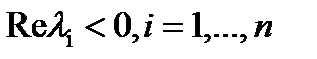 
, ( 
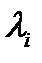- собственные числа матрицы A–LC). Тогда при любых фиксированных q1, q2 таких, что 
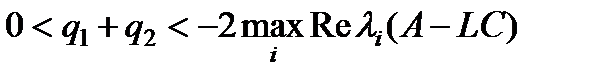эллипсоидальная оценка
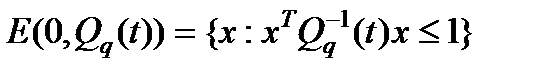(2.6)
где Q(t)=Qq(t) – решение матричной системы сравнения (2.5) с Qq(t0)=Q0>0, ограничена и сходится к предельному эллипсоиду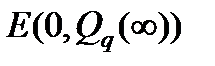 
, где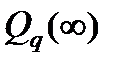 
- решение алгебраического матричного уравнения Ляпунова (уравнения равновесия для (2.5))
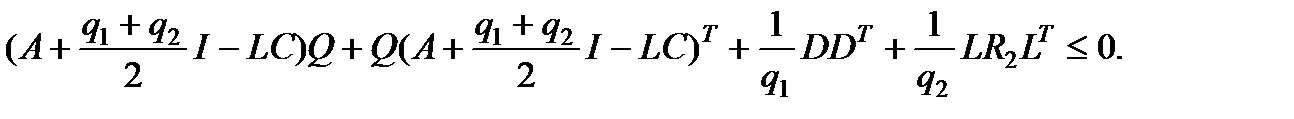(2.7)
В рассматриваемом частном случае линейных автономных систем, справедлива следующая теорема.
Теорема 2.2. Решение Q* и Y* задачи минимизации
Tr(Q) —> min
при ограничениях
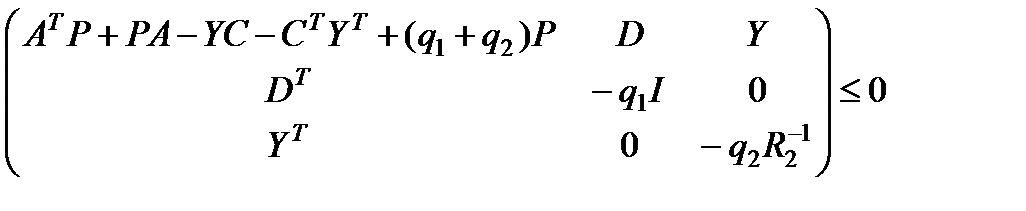, (2.8)
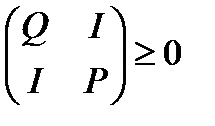, (2.9)
где минимизация проводится по матричным переменным Q=QT, P=PTÎRn´n, YÎRn´k, и числовым параметрам q1,q2, определяет матрицу Q* минимального инвариантного эллипсоида, а также соответствующую этому эллипсоиду матрицу L=Q*Y* коэффициентов наблюдателя состояния (2.4) и параметры q1,q2.
Для решения задач оптимизации с ЛМН (2.8), (2.9) применяется пакет CVX для Matlab [6]. Фрагмент программы для синтеза параметров наблюдателя представлен ниже.
% Синтез наблюдателя состояния для линеаризованной системы на основе
% решения ЛМН
step1 = 0.05;
step2 = step1;
begin_val1 = 0.15;
end_val1 = 0.25;
begin_val2 = 0.4;%
end_val2 = 0.6;
min_tr_Z = 1000000;
figure (4)
% Оптимизация по параметрам q1 и q2 путем перебора с уменьшающимся шагом
while ((step1+step2)>0.05)
for q1 = begin_val1:step1:end_val1
for q2 = begin_val2:step2:end_val2
cvx_begin sdp
variable Qs(n1, n1) symmetric;
variable Ps(n1, n1) symmetric;
variable Ys(n1, 1) ;
minimize( trace(Qs))
subject to
Qs >= eye(2)*1e-8;
[A'*Ps + Ps*A-Ys*Cy-Cy'*Ys'+(q1+q2)*Ps Ps*D Ys;
D'*Ps -q1 0;
Ys' 0 -q2*R2_1]< 0; %условие асимптотич устойчивости
[Qs eye(2);
eye(2) Ps]>=0.0;
cvx_end
Qsf = double(Qs)
Psf = double(Ps)
Y=double(Ys);
L=Qsf*Y
trZ=trace(Qsf);
if min_tr_Z > trZ
min_tr_Z = trZ
Q_min = Qsf;
P_min = Psf;
L_min=L;
q_min1 = q1
q_min2 = q2
end;
end;
step1= step1*0.5;
begin_val1 = q_min1-2*step;
end_val1 = q_min1+2*step;
end;
step2= step2*0.5;
begin_val2 = q_min2-2*step;
end_val2 = q_min2+2*step;
end;
QL=Q_min
PL=P_min
L1=L_min
q01=q_min1;
q02=q_min2;
AL1=A-L1*Cy;
eig(AL1)
E = ellipsoid(QL);
%pEs = projection(E, BB);
plot(E, 'r');grid on;hold on;
Для рассматриваемого примеры с использованием указанной программы в пакете MatLab были получены значения параметров q1 =0.25 q2 =0.6, матрицы
, 
, 
,
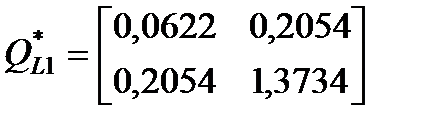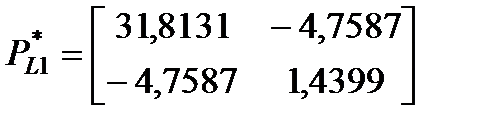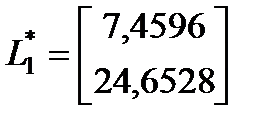при которых достигается минимум следа матрицы предельного инвариантного эллипсоида для ошибки оценивания. При этом матрица A–LC наблюдателя имеет собственные значения -–3.7390 ± 3.35302i, что говорит об ее гурвицевости. Предельный инвариантный эллипс, ограничивающий ошибку оценивания, показан на рисунке 2.1.
Рисунок 2.1. Минимальный инвариантный эллипс для ошибки оценивания
С помощью вызова функции Observ_Mayat_Integr_01, текст которой представлен ниже
% моделирование нелинейной системы с наблюдателем
x0 = [5; 2;0;0;];
x=Observ_Mayat_Integr_01(n,x0,w0,K1,L1,Cy,0,5,7);
function y= Observ_Mayat_Integr_01(n,x,w0,K1,L1,Cy,t0,tk,k)
%Функция для интегрирования нелинейной модели маятника с регулятором и наблюдателем
[t,x] = ode45(@(t,x) Prav_Nabl_NL_Mayat_1(t,x,w0,K1,L1,Cy),[t0 tk],x);
% hs = size(H);
y = [];
nh=length(x(:,1));
t(nh)
figure (k)
plot(t,x(:,1),'b');grid on;hold on;
plot(t,x(:,2),'r');grid on;hold on;
plot(t,x(:,3),'y');grid on;hold on;
plot(t,x(:,4),'g');grid on;hold on;
y=[x(nh,1); x(nh,2);x(nh,3);x(nh,4)];
end
получены переходные процессы в исходной системе с регулятором и наблюдателем как без учета внешних возмущений и погрешностей измерений (показаны на рисунке 2.2), так и при действии внешнего возмущения w=-sin(2*cos(3*t)) и погрешностей измерений, задаваемых датчиком случайных чисел (показаны на рисунке 2.3).
Рисунок 2.2. Переходные процессы в исходной системе с регулятором по состоянию (синий и красный) и наблюдателе (черный и зеленый) при отсутствии возмущений и погрешностей измерений
Рисунок 2.3. Переходные процессы в исходной системе с регулятором по выходу наблюдателя (синий и красный) и наблюдателе (черный и зеленый) при действии возмущений и погрешностей измерений
Для вычисления правых частей исходной системы дифференциальных уравнений и уравнений наблюдателя использовалась функция Prav_Nabl_NL_Mayat_1, текст которой представлен ниже.
function dx=Prav_Nabl_NL_Mayat_1(t,x,w0,K1,L1,Cy)
% Вычисление правой части исходной нелинейной системы с
% регулятором, заданным матрицей K1, наблюдателем с матрицей L1, и внешними возмущениями, заданными переменной w
x1=[x(1);x(2)];
xn=[x(3);x(4)];
u=K1*xn;
w=-sin(2*cos(3*t));
ksi=(0.5-rand(1))/5000;
y=Cy*x1+ksi;
dx1=x(2);
dx2=-w0*sin(x(1))+u+w;
dx3=x(4)+L1(1)*(y-Cy*xn);
dx4=-w0*x(3)+u+L1(2)*(y-Cy*xn);
dx=[dx1;dx2;dx3;dx4];
end