Прогнозирование гранулометрического состава по уровню удельного расхода ВВ

Чрезвычайно сложная задача определения эффективности-действия взрыва в горных породах не решается методами механики даже для одного заряда. для ее решения необходимо использовать дополнительные предположения о статистике дефектов и форме взаимодействия взрывного импульса с этими дефектами.

В технологической задаче прогнозирования результатов взрывного дробления рассматривается совокупное действие системы разновременно инициируемых зарядов ВВ, взрывные импульсы которых взаимодействуют, Это требует учета множества факторов, тем или иным способом влияющих на образование горной массы. Если даже не рассматривать факторы связанные с распределением свойств массива, то остаются параметры буровзрывных работ: геометрические параметры, энергетические характеристики и конструктивные особенности зарядов ВВ, способ инициирования, характер забойки и т.д.

Полный перечень этих параметров включает около 20 наименований, среди которых необходимо выделить наиболее существенные. Выбор этот происходит пока достаточно произвольно, в результате чего время от времени появляются работы, устанавливающие эмпирические зависимости между показателями кусковатости и той или иной характеристикой заряда, причем каждый раз предполагается, что эта характеристика определяющая.

Современные теории действия взрыва в горных породах не могут пока установить чисто теоретические закономерности формирования совокупности кусков горной массы при взрыве. Существующие зависимости имеют эмпирический характер и получены часто путем обработки данных производственных взрывов.

Установить эмпирическую зависимость между характеристиками гранулометрического состава и 20 взаимосвязанными параметрами БВР невозможно, даже существенно уменьшив число параметров БВР. Поэтому чаще всего стараются получить простые формулы, связывающие, как правило, одну характеристику кусковатости (средний размер, выход негабарита, выход кондиционных кусков) с одной обобщающей характеристикой БВР через коэффициенты, устанавливающие свойства горных пород и технологиче­ские особенности разрушения. В таких случаях предполагается, что при изменении этого обобщающего показателя другие остаются постоянными или варьируют незначительно.

Выделение наиболее существенных показателей буровзрывных работ потребовало экспертной оценки, материалы которой определили в качестве наиболее важных геометрические (сетку бурения и диаметр скважин) и энергетические (удельный расход и тип ВВ) параметры. При этом оценка специалистов на первое место единодушно поставила удельный расход ВВ как наиболее существенный обобщающий параметр БBP, с наибольшей полнотой позволяющий оценить совокупное влияние системы зарядов ВВ.

Отечественная практика БВР ограничена в выборе средств бурения скважин. На карьерах, например, 70 % горной массы обуривается станком СБШ-250 с диаметром долота 243 мм, а остальной объем бурения - по преимуществу станком СБШ-200 с диа­метром долота 214 мм. В этих условиях уровень удельного расхода ВВ является тем обобщающим показателем при неизменной высоте уступа, который определит и сетку бурениями массу заряда в скважине, и т.п.

Эмпирические зависимости, связывающие характеристики дробления с удельным расходом В3 имеет самую разную форму. Наиболее простая линейная зависимость имеет вид

V_H=V_e+(1-kq) (42)

где V_H - содержание негабаритных кусков после взрыва, %; Ve -содержание крупных отдельностей в массиве, %; k - эмпирический коэффициент; q - удельный расход ВВ, при котором выход фракции +500 будет близок к нулю.

При переcчете удельного расхода на другой размер куска в формулу (42) вводится поправка 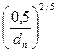(здесь d_n - требуемый размер куска).

Простой способ определения зависимости q от dср предлагает и Г.В.Кузнецов. Не пытаясь определить физический смысл нелинейности, он аппроксимирует эту зависимость параболой типа

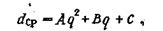(43)

где А , В, С - коэффициенты, характеризующие свойства разру­шаемых пород и порядок ведения взрывных работ.

Наибольшее распространение получила гиперболическая зависимость, предложенная Л.И.Бароном, где устанавливается связь между выходом негабарита и удельным расходом:

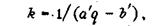(44)

где а и о - эмпирические коэффициенты, характеризующие свойства массива и параметры отбойки.

Каждая из этих аппроксимаций получена на основании обработки достаточно большого количества производственных взрывов, а разница в форме зависимостей объясняется, по-видимому, большим разбросом экспериментальных данных.

Попытки теоретического определения связи между кусковатостью горной массы и параметром удельного расхода ВВ на основе гидродинамической модели действия взрыва дают другую форму зависимости (В.Н.Кузнецов)

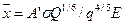(45)

Где X - математическое ожидание размера куска; А’ - эмпирический коэффициент, зависящий от прочности горных пород; 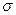-прочностная характеристика массива пород; Q - масса заряда в скважине; Е- модуль Юнга.

Другая зависимость, полученная на основе рассмотрения двухнедельного распределения (В.А.Безматерных)

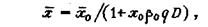(46)

где х₀ - средние размеры отдельностей в массиве; β₀- коэффициент, учитывающий условия взрывания и свойства пород; D -скорость детонации.

Можно отметить еще одну зависимость, полученную на основе статистико-вероятностной модели разрушения (В.А.Падуков, В.П.Макарьев), по которой для идентичных массивов пород связь между средним размером куска и удельным расходом ВВ определяется экспоненциальной зависимостью

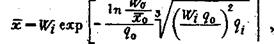
(47)

где W₀, и W_i - параметры сетки скважины (ЛНС,Öab ) эталонного и прогнозируемого взрывов; q₀ и q_?- - удельные энергозатраты на отбойку эталонного и прогнозируемого взрывов; а и b -расстояния между скважинами в ряду и между рядами скважин (параметр сетки взрывных скважин); х и х₀- математические ожидания размеров кусков горной массы эталонного и прогнозируемого взрывов.

Анализируя зависимости (42)-(46), можно установить, что, в основном, они мало отличаются одна от другой. Разница между гиперболической зависимостью в виде (44) или (46) и линейной (42) объясняется, вероятно, большим разбросом экспериментальных данных в том узком диапазоне Изменений удельного расхода ВВ в пределах которого определялись эти зависимости.

Большой материал производственных исследований, посвященныхэтому вопросу, позволяет достаточно точно установить значения эмпирических коэффициентов, в пределах которых резуль­таты расчетов по различным формулам мало отличаются один от другого.

Важной особенностью всех этих зависимостей является то, что все коэффициенты в них не имеют ясного физического смысла. Их получают путем обработки большого количества результатов массовых взрывов. Таким образом, прогнозирование среднего размера куска горной массы, а следовательно, и гранулометрического состава, носит интерполяционный характер, т.е. прогнозируемые результаты должны находиться внутри того диапазона параметров, по которым определяются эмпирические коэффициенты.

В наиболее чистом виде это обстоятельство формулируется как прогнозирование по эталонному взрыву или эталонной совокупности взрывов. Здесь слово эталон означает идентичность свойств горных пород и условий ведения взрывных работ, т.е. примерное постоянство тех параметров БВР, которые не входят в зависимость.

В формуле (47), например, исходные данные для прогнозирования кусковатости целиком задаются параметрами эталонного взрыва, по каждому из которых определены соответствующие характеристики кусковатости. Таким образом, прогнозирование ведется от достигнутого уровня.

Необходимо отметить, что этот общий принцип прогнозирования дает наиболее устойчивые результаты, особенно в том случае, когда имеется достаточно большой и непрерывно пополняющийся производственный опыт.