Экстремум функции двух переменных. Необходимый признак.Если функция двух переменных z=f(x,y) имеет экстремум в точке

Необходимый признак.Если функция двух переменных z=f(x,y) имеет экстремум в точке, то каждая ее частная производная первого порядка в этой точке равна нулю или не существует.

Достаточный признак.Чтобы установить имеет ли функция z=f(x,y) экстремум в критической точке, нужно найти вторые производные этой функции по x, по y и смешанную производную

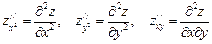
Затем проверить знак выражения

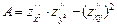
Если A>0 и 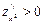, то функция в точке имеет минимум. Если A>0 и 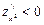, то функция в точке имеет максимум. Если A<0, то экстремума нет.

Пример 6.2.

Исследовать функцию z = y⁴ - 2xy² + x² + 2y + y² на экстремум.

Решение.

Находим частные производные:

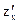= - 2y² + 2x; 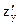= 4y³ - 4xy +2 +2y.

Для отыскания критических точек решим систему уравнений:

.

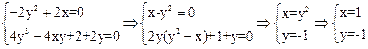Итак, M_o(1,-1) -единственная точка, «подозрительная на экстремум».

Находим вторые частные производные в найденной точке:

.

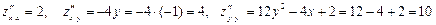Проверим знак выражения

.

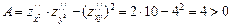Так как A>0 и 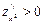, то функция в точке M_o(1,-1) имеет минимум.

Вычислим z _min = (-1)⁴ - 2×1×(-1)² +1 - 2 +1 = -1.

Условный экстремум функции двух переменных

Пусть необходимо найти экстремум функции z=f(x,y) при условии g(x,y)=0.

Функция z=f(x,y) называется целевой функцией.

Первый метод решения – метод подстановки, применяется, когда из уравнения g(x,y)=0 можно выразить переменную y=φ(x) и подставить ее в целевую функцию. Таким образом, решение сводится к нахождению экстремума функции одной переменной.

Второй метод – метод множителей Лагранжа, используется, когда нельзя явно выразить y из условия g(x,y)=0. В этом случае, для решения вводится новая функция Лагранжа.

,

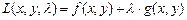где λ – неопределенный множитель, новая переменная.

Затем находится экстремум этой функции от трех переменных.

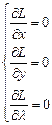
Решая эту систему, получают значения критической точки условного экстремума функции z=f(x,y).

После этого определяется максимум или минимум функции z=f(x,y) в этой точке по смыслу задачи.

Пример 6.3.

Найти экстремумы функции 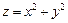при условии .

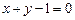Решение.

Выразим переменную у из условия 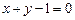и подставим в функцию:

; .

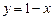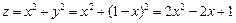Получим функцию одной переменной. Найдем ее экстремум.

; , .

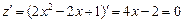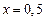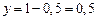Так как вторая производная 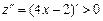, то найденная точка - точка минимума.

Следовательно, функция 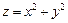имеет условный минимум в точке 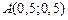, который равен .

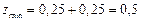Пример 6.4. На 2 товара - Кириешки ( 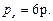) и чипсы ( 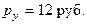) Сергей тратит в месяц 120 руб. Определить оптимальный выбор, если его функция полезности .

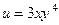Решение.

Необходимо найти максимум функции 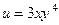при условии 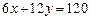. Воспользуемся функцией Лагранжа.

.

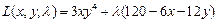Найдем частные производные от функции Лагранжа:

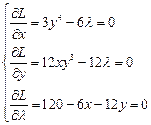
Решаем полученную систему.

.

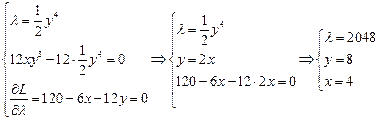Таким образом, оптимальный выбор составит 4 ед. Кириешки и 8 ед. чипсов, при этом оптимальное значение функции полезности составит 49152.

Варианты контрольной работы

Вариант 0

1. Вычислить предел функции

а) ;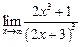

б) ;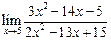

в) .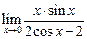

2. Вычислить производную функции

a) ;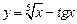

б) ;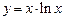

в) ;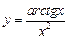

г) .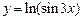

3. Исследовать функцию и построить график .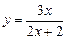

4. На 2 товара - кириешки ( 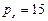руб.) и чипсы ( 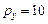руб.) Сергей тратит в месяц 120 руб. Определить набор продуктов, обеспечивающий максимальную полезность, если функция полезности .

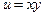Вариант 1

1. Вычислить предел функции

а) ;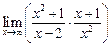

б) ;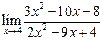

в) ;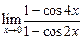

2. Вычислить производную функции

а) 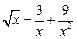;	б) ;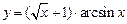
в) 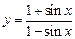;	г) .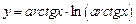

3. Исследовать функцию и построить график .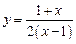

4. На 2 товара - колбасу ( 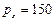руб.) и сыр ( 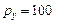руб.) Сергей тратит в месяц 300 руб. Определить набор продуктов, обеспечивающий максимальную полезность, если функция полезности .

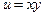Вариант 2

1. Вычислить предел функции

а) ;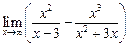

б)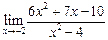

в) .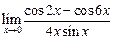

2. Вычислить производную функции

а) 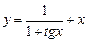;	б) ;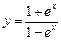
в) 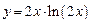;	г) .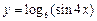

3. Исследовать функцию и построить график .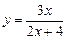

4. Средняя семья тратит 30 долл. в месяц на рыбу и хлеб. Цена рыбы 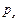- 5 долл., цена батона хлеба 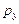- 1 долл. Определить набор продуктов, обеспечивающий максимальную полезность, если функция полезности имеет вид: .

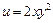Вариант 3

1. Вычислить предел функции

а) ;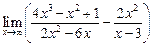

б) ;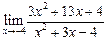

в)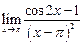

2. Вычислить производную функции

а) 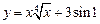;	б) ;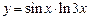
в) 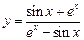;	г) .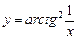

3. Исследовать функцию и построить график .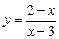

4. На 2 товара - компакт-диски ( 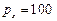руб.) и аудиокассеты ( 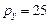руб.) Влад тратит в год 1000 руб. Определить набор продуктов, обеспечивающий максимальную полезность, если функция полезности .

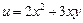Вариант 4

1. Вычислить предел функции

а) ;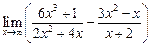

б) ;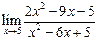

в) .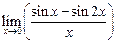

2. Вычислить производную функции

а) 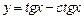;	б) ;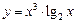
в) 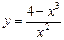;	г) .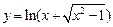

3. Исследовать функцию и построить график .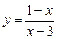

4. За месяц студент расходует на апельсины и бананы 100 рублей. Цена одного апельсина 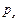5 р, а цена одного банана 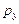2 р. Определить набор продуктов, обеспечивающий максимальную полезность, если функция полезности u=10ху.

Вариант 5

1. Вычислить предел функции

а) ;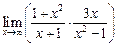

б) ;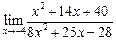

в) .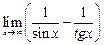

2. Вычислить производную функции

а) 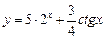;	б) 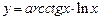;	в) ;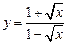
г)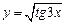

3. Исследовать функцию и построить график .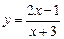

4. На 2 товара – видеокассеты и аудиокассеты Олег тратит еженедельно 50 руб. Цена видеокассеты 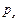15 руб., цена аудиокассеты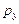

5 руб. Определить набор кассет, обеспечивающий максимальную полезность, если функция полезности u = 2xy.

Вариант 6

1. Вычислить предел функции

а) ;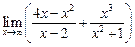

б) ;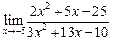

в) .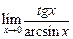

2. Вычислить производную функции

а) 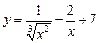;	б) ;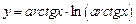
в) 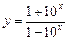;	г) .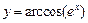

3. Исследовать функцию и построить график .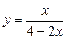

4. На два товара – молоко и хлеб Иван тратит 200 ден. ед. в месяц. Цена молока 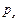– 20 ден. ед., хлеба 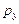– 15. Определить набор продуктов, обеспечивающий максимальную полезность, если функция полезности .

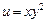Вариант 7

1. Вычислить предел функции

а) ;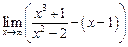

б) ;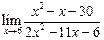

в) .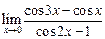

2. Вычислить производную функции

а) 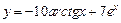;	б) ;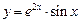
в) 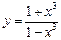;	г) .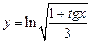

3. Исследовать функцию и построить график .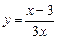

4. Ольга тратит еженедельно 200 руб. на бананы и пепси-колу. Цена 1 кг бананов 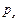–30 руб., 1 л пепси 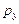– 20 руб. Определить набор продуктов, обеспечивающий максимальную полезность, если функция полезности .

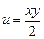Вариант 8

1. Вычислить предел функции

а) ;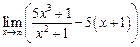

б) ;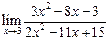

в)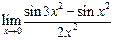

2. Вычислить производную функции

а) 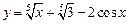;	б) ;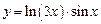
г) 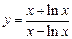;	г) .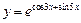

3. Исследовать функцию и построить график .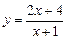

4. На 2 товара - мясо ( 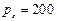руб.) и сыр ( 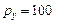руб.) Оля тратит в месяц 3000 руб. Определить набор продуктов, обеспечивающий максимальную полезность, если функция полезности .

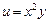Вариант 9

1. Вычислить предел функции

а) ;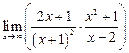

б) ;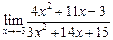

в) .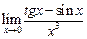

2. Вычислить производную функции

а) 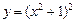;	б) ;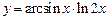
в) 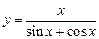;	г) .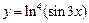

3. Исследовать функцию и построить график .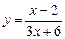

4. На 2 товара - яблоки ( 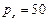руб.) и сливы ( 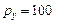руб.) Оксана тратит в месяц 500 руб. Определить набор продуктов, обеспечивающий максимальную полезность, если функция полезности .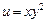