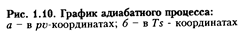Изотермический процесс

Процесс, протекающий при постоянной температуре рабо­чего тела, называется изотермическим. Он возможен, напри­мер, в цилиндре поршневой машины, если по мере подвода теплоты к рабочему телу поршень перемещается, увеличивая при этом объем настолько, что температура остается неизмен­ной. График изотермического процесса pv- и Ts-диаграмм называется изотермой. Уравнение изотермического процесса может быть получено из уравнения Клапейрона, если принять температуру постоянной (T = idem):

согласно (1.73) изотермический процесс в рv-диаграмм (рис. 1.9) изображается в виде равнобокой гиперболы, рас положенной симметрично относительно координатных осей.

Из уравнения (1.73) следует:

1аким образом, при постоянной температуре рабочего тела давление изменяется обратно пропорционально его удельному объему.

Работа расширения газа l (см. рис. 1.9, а) графически изображается площадью, ограниченной линией процесса (1 - 2 расширение,1 - 2' - сжатие) и осью абсцисс.

Формула для подсчета работы расширения l 1 кг газа в изотермическом процессе может быть записана в следующем виде:

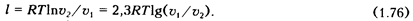
Для G (кг) газа формула (1.76) приобретает вид

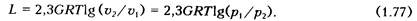
Изменение внутренней энергии в изотермическом процессе идеального газа

так как T = T = idem.

Количество теплоты q, сообщенной газу в данном про­цессе, определяется из выражения первого закона термодина­мики с учетом формул (1.76) и (1.77):

Следовательно, в изотермическом процессе вся теплота, сообщаемая газу, расходуется полностью на работу рас­ширения.

Изменение энтальпии (Δh 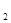= h – h 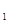) идеального газа в изотермическом процессе с учетом формулы (1.69) равно нулю:

В Ts-диаграмме (см. рис. 1.9, б) изотерма изображается го­ризонтальной линией относительно оси абсцисс, подводимая теплота (+ q) ~ площадью 1, 2, 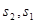, а отводимая теплота (- q) - площадью 1,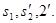

Изменение удельной энтропии в изотермическом процессе подсчитывают по уравнению

АДИАБАТНЫЙ ПРОЦЕСС

Адиабатным называется процесс, который осуществляется без теплообмена между газом и внешней средой (q = 0). Практическое использование этот процесс находит в соплах паровых турбин, реактивных двигателей и в других случаях, когда газ движется с высокими скоростями. Уравнение адиабаты имеет вид

где k = С /C - показатель адиабаты (для одноатомных газов k = 1,67, для двухатомных k = 1,41, для трех- и более атомных газов k = 1,29).

Практически адиабатный процесс можно осуществить при расширении или сжатии газа в цилиндре, стенки которого не проводят теплоты, или при протекании процесса настолько быстро (мгновенно), что теплообмен между рабочим телом и окружающей (внешней) средой не успевает произойти.

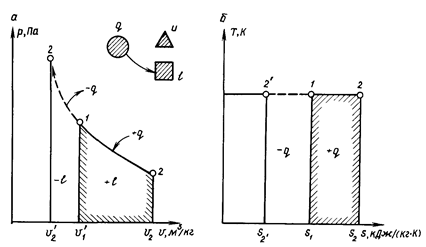
В jou-диаграмме (рис. 1.10, а) адиабата изображается неравнобокой гиперболой. Из сравнения адиабаты и изотермы видно, что давление в адиабатном процессе изменяется быстрее, чем в изотермическом.

Связь между параметрами состояния рабочего тела в адиа­батном процессе устанавливается из уравнения (1.82):

Изменение внутренней энергии рабочего тела определяют по выражению

Работа расширения / газа в адиабатном процессе может быть найдена из выражения первого закона термодинамики:

Отсюда

Так как согласно (1.36) C 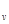= R/(k – 1), то

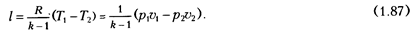
Следовательно, в адиабатном процессе расширения работа совершается за счет уменьшения внутренней энергии газа, т.е.

Т2 < T1

В обратном процессе сжатия работа, совершаемая внешней

средой над газом, идет на увеличение внутренней энергии рабочего тела, повышение его температуры.

Работа расширения газа - положительная (+ l) работа сжатия – отрицательная

(- l).

ПОЛИТРОПНЫЙ ПРОЦЕСС

Во всех реальных теплов­ых машинах (двигателях внутреннего сгорания - ДВС, компрессорах, газотурбинных установках и т.д.) процессы сжатия рабочего тела (газа), горения топлива, расширения рабочего тела являются политропными.

Политропный процесс обратимый и выражается уравнением

где показатель п может принимать любое значение от - ∞ до + ∞. Для каждого процесса показатель п - величина постоянная.

Все описанные ранее процессы (изохорный, изобарный, изотермический и адиабатный) являются частными случаями политропного процесса с показателями политропы п соот­ветственно ± ∞; 0; 1; k.

Поскольку уравнение политропного процесса (pv 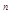= idem) совпадает по форме с уравнением адиабатного процесса (pv 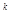= idem), то связь между параметрами состояния газа в поли­тропном процессе может быть выражена формулами, аналогич­ными формуле (1.83):

То же самое относится и к выражению для работы рас­ширения l в политропном процессе:

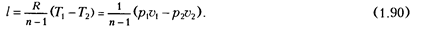
Изменение внутренней энергии в политропном процессе определяется общим выражением

Количество теплоты в процессе может быть вычислено на основании первого закона термодинамики:

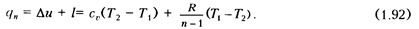
Чтобы подсчитать теплоемкость газа (рабочего тела) в политропном процессе с 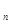, используют формулу

С учетом формулы (1.92) выражение принимает вид

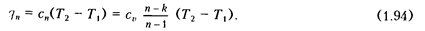
Изменение энтропии в политропном процессе может быть найдено из выражения