Тема 2. Графический метод решения задач линейного программирования

I. Пояснительная записка. Целевая установка.

Данное пособие содержит учебно-методические рекомендации по изучению курса «Линейное программирование» для студентов экономического факультета по специальностям «Экономика и управление на предприятии», «Бухгалтерский учёт и аудит», «Прикладная информатика в экономике». Пособие содержит теоретический материал, иллюстрированный примерами решения основных задач с экономическим содержанием.

Целевая установка.

Цель пособия – оказать помощь студентам в изучении курса «Линейное программирование» для развития навыков по применению различных математических методов и моделей в решении задач торгово-коммерческой и управленческой экономической деятельности, а также подготовить студентов к самостоятельному изучению литературы по математическим методам в экономике.

В результате изучения дисциплины каждый студент должен

знать: возможности экономико-математического аппарата и принципы его использования при самостоятельной постановке простейших экономических задач;

уметь: формализовать и решать экономические задачи с использованием экономико-математического аппарата.

II. Программа:

1) Моделирование экономических процессов коммерческого предприятия.

2) Решение задачи ЛП на основе её геометрической интерпретации.

3) Решение моделей симплексным методом.

4) Двойственная задача к задаче планирования работы коммерческого предприятия.

5) Транспортная задача. Построение первого опорного плана. Нахождение оптимального плана.

III. Рекомендуемая литература.

1) Ляшенко И.Н. «Линейное и нелинейное программирование», - Киев: «Вища школа», 1975.

2) Кузнецов Ю.Н. «Математическое программирование», - М: «Высшая школа», 1976.

3) Лунгу К.Н. «Линейное программирование (руководство к решению задач)», - М: «Физматлит», 2005.

4) Плотников А.Д. «Математическое программирование», - Минск: «Новое знание», 2006.

5) Красс М.С., Чупырнов Б.П. «Математика для экономистов», - С-Пб: «Питер», 2007.

6) Палий И.А. «Линейное программирование», - М: «Эксмо», 2008.

IV. Методические указания.

Тема 1. Общее линейное программирование (ЛП).

Основные понятия и определения.

Определение. Линейное программирование – это область математического программирования (т.е. поиск некоторой программы действий), являющаяся разделом математики, в котором изучаются методы исследования и отыскания экстремальных (наибольших и наименьших) значений некоторой линейной функции, на аргументы которой наложены линейные ограничения.

Такая линейная функция называется целевой, а набор количественных соотношений между переменными, выражающих определённые требования экономической задачи в виде уравнений или неравенств, называется системой ограничений.

Определение. Совокупность соотношений, содержащих целевую функцию и ограничения на её аргументы, называется математической моделью экономической задачи оптимизации.

В общем виде математическая модель задачи линейного программирования записывается как

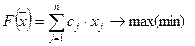при условиях-ограничениях

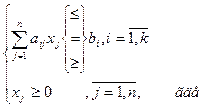
a_ij, b_i, c_j – заданные постоянные величины.

Определение. Стандартной (или симметрической) задачей ЛП называется задача, имеющая вид

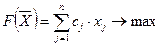
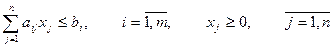
или

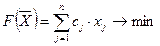
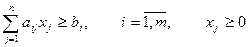
Определение. Канонической (или основной) задачей ЛП называется задача, имеющая вид

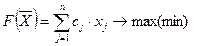
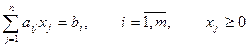
Стандартную задачу можно привести к каноническому виду, вводя дополнительные (или вспомогательные) переменные в левые части неравенств.

Определение. Совокупность чисел 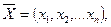при котором целевая функция принимает максимальное (минимальное) значение называется оптимальным решением задачи ЛП.

Всякая же другая совокупность значений, удовлетворяющая ограничениям определяет допустимое решение (план).

Примеры задач ЛП.

Для составления математической модели задачи ЛП необходимо выполнить следующие шаги:

- обозначить переменные;

- составить целевую функцию в соответствии с целью задачи;

- записать систему ограничений с учётом имеющихся в условии задачи показателей.

Рассмотрим ряд наиболее распространённых задач.

Пример1. Задача об использовании сырья.

Предположим, что изготовление продукции двух видов P₁ и P₂ требует использования четырёх видов сырья S₁,S₂,S₃ и S₄. Запасы сырья каждого вида ограничены и составляют соответственно b₁,b₂,b₃,b₄ условных единиц.

Количество единиц сырья, необходимое для изготовления единицы каждого из видов продукции известно и задаётся таблицей 1.

Табл.1

Виды сырья	Запасы сырья	Виды продукции
P1	P2
S1 S2 S3 S4	b1 b2 b3 b4	a11 a21 a31 a41	a12 a22 a32 a42
Доход	c1	c2

Здесь 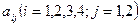означает количество единиц сырья вида S_i, необходимое для изготовления продукции P_j. В последней строке таблицы указан доход, получаемый предприятиям от реализации одной единицы каждого вида продукции.

Требуется составить такой план выпуска продукции видов P₁ и P₂, при котором доход предприятия от реализации всей продукции оказался бы максимальным.

Математическую модель поставленной задачи изучим на следующем числовом примере (табл.2).

Табл.2

Виды сырья	Запасы сырья	Виды продукции
P1	P2
S1 S2 S3 S4
Доход

Допустим, что предприятие выпускает x₁ единиц продукции вида P₁ и x₂ единиц продукции вида P₂.

Для этого потребуется 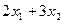единиц сырья S₁.

Так как в наличии имеется всего 20 единиц сырья S₁, то должно выполняться неравенство

.

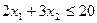Неравенство (а не точное равенство) появляется в связи с тем, что максимальный доход может быть достигнут предприятием и в том случае, когда запасы сырья S₁ используется не полностью.

Аналогично получаем неравенства для других видов сырья

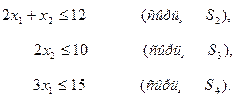
При этих условиях доход F, получаемый предприятием, составит

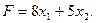
Таким образом, математическую задачу можно сформулировать так: дана система четырёх линейных неравенств

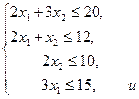
линейная целевая функция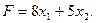

Требуется среди неотрицательных (из самого смысла величин x₁ и x₂ очевидно, что 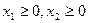) решений системы выбрать такое, при котором функция F принимает наибольшее значение, т.е.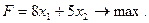

Пример2. Задача о распиле.

Для изготовления брусьев длины 0.2,0.3 и 0.5 м на распил поступили брёвна длиной 1 м. Нужно получить не менее 200 и не более 300 брусьев длиной 0.2 м, не менее 300 и не более 400 длиной 0.3 м, не менее 400 и не более 500 длиной 0.5 м. Как распиливать брёвна, чтобы обеспечить нужное количество брусьев каждого размера и при этом минимизировать отходы?

Рассмотрим все способы распила одного бревна. Например, бревно длиной 1 м можно распиливать на 2 бруска длиной по 0.5 м, при этом отходов нет. Или можно распилить на 3 бруска длиной по 0.3м, тогда в отходы уйдёт по 0.1 м бревна.

Все варианты распила приведены в таблице 3.

Табл.3

Способ распила	Количество брусьев длиной	Величина отходов, м
0.2 м	0.3 м	0.5 м
				0.1
				0.1
				0.1

Опишем математическую модель задачи.

Обозначим через x_j (j= 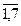) количество бревен, распиленных j-тым способом. Всего 7 неизвестных, каждое из которых может принимать только целые значения. Требуется минимизировать суммарные отходы. Отходы остаются только при 2, 4 и 6 способах распила. Поэтому суммарная величина равна

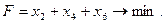
Всего брусьев длиной 0.2 м будет получено 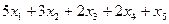штук. По условию этих брусьев должно быть не менее 200 и не более 300, получаем два ограничения:

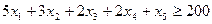
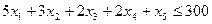
Аналогично строим ограничение по числу брусьев длиной 0.3 м и 0.5 м.

,

,

,

.

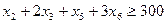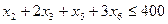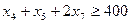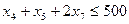Учитываем также условия неотрицательности и целочисленности переменных: , , .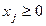

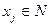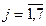Изменим условие задачи.Пусть потребуется ровно 200 брусьев длиной 0.2 м, 300 брусьев длиной 0.3 м, 400 брусьев длиной 0.5 м и при этом минимизировать суммарные отходы.

Пусть снова x₁, x₂,…x₇ – количество бревен, распиленных по 1,2…7-му способам соответственно. Тогда количество брусьев длиной 0.2, 0.3 и 0.5 м будет соответственно таким:

5x₁ +3x₂ +2x₃ +2x₄ +x₅ ;

x₂ +2x₃ +x₅ +3x_{6 ;}

x₄ +x₅ +2x₇.

Таким образом, нельзя гарантировать, что в результате распила получится, например, ровно 200 брусьев длиной 0.2м, можно потребовать только, чтобы их было не менее 200 штук. Но если их будет 202 штуки, то получится ещё 0.4 дополнительных единиц отходов. Обозначим через y_1, y₂ и y₃ избыточные количества брусьев длиной 0.2 м, 0.3 м и 0.5 м. Они привнесут в целевую функцию дополнительно 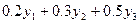единиц отходов.

Окончательно целевая функция имеет вид:

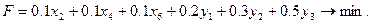
Система ограничений имеет вид:

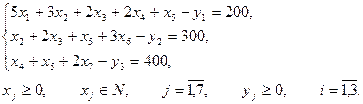
Всё это составляет математическую модель данной задачи.

Пример3. Задача о питании.

Для сохранения здоровья и работоспособности человек должен потреблять в сутки определённое количество питательных веществ, например, белков, жиров, углеводов, воды и витаминов. Запасы этих ингредиентов в различных видах пищи различны. Попробуем составить диету, содержащую, по крайней мере, 20 единиц белков, 25 единиц углеводов, 10 единиц жиров, 15 единиц воды и 30 единиц витаминов. Как дешевле всего составить диету из 5 наименований продуктов: хлеба, овощей, рыбы, фруктов, молока: В таблице 4 указаны цены продуктов на 1 кг (или 1 литр) в денежных единицах и содержание в продуктах компонентов диеты в условных единицах.

Табл.4.

Питательные вещества	Норма	Продукты
Хлеб, P1	Овощи, P2	Рыба, P3	Фрукты, P4	Молоко, P5
Белки, B1	b1=20
Углеводы, B2	b2=25
Жиры, B3	b3=10
Вода, B4	b4=15
Витамины, B5	b5=30
Цена	-	c1=24	c2=36	c3=64	c4=75	c5=10

Предположим далее, что стоимость некоторой единицы продукта вида P_j составляет c_j. Требуется так организовать питание, чтобы его стоимость была наименьшей, но организм получил бы не менее минимальной суточной нормы питательных веществ всех видов B_i.

Пусть x₁, x₂, x₃, x₄, x₅ – количество продуктов вида P_j, приобретаемых и потребляемых человеком. В этом случае общие запасы белков составляют

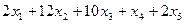и не должны быть меньше минимальной нормы b₁=20. Это требование приводит к неравенству

.

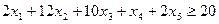Знак « 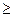» возникает потому, что при выбранной системе питания в приобретенной пище белков может быть и больше минимальной нормы, аналогично получим и другие неравенства:

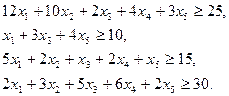
При этом общая стоимость питания равна:

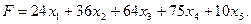
Итак, мы пришли к следующей математической модели. Задана система пяти линейных неравенств с пятью неизвестными вида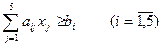

Требуется найти среди всех неотрицательных решений системы такое, которое сообщает целевой функции F наименьшее значение, т.е.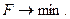

Пример4. Транспортная задача.

Требуется доставить железную руду с трёх месторождений четырём заводам. Стоимость перевозки (ден.ед.) 1 т руды от каждого месторождения каждому заводу задана таблицей 5.

Табл.5

Месторождения	Завод
I
II
III

Запасы добытой руды на месторождениях за некоторый промежуток времени составили 200, 200 и 300 т соответственно. Потребности заводов за тот же период времени были такими: 100, 200, 100 и 300 т. Как организовать поставку руды заводам, чтобы минимизировать стоимость перевозок?

Построим математическую модель задачи.

Учитываем, что общий запас руды в месторождениях равен потребности в ней всех 4 заводов.

Требуется составить такой план перевозок, при котором их общая стоимость была бы наименьшей.

Обозначим через x_ij количество единиц груза (т руды), предназначенного к отправке с месторождений A_i на заводы B_j. Построим матрицу перевозок (Таблица 6)

Табл.6

Месторождения	Заводы	Запасы
B1	B2	B3	B4
A1	x11	x12	x13	x14
A1	x21	x22	x23	x24
A1	x31	x32	x33	x34
Потребности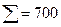

Из условий задачи с очевидностью вытекает, что общая стоимость F всех видов перевозок равна

(*)

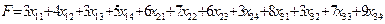Количество тонн руды, которая планируется к доставке на завод B₁ со всех трех месторождений составит

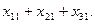
Но так как потребность в руде на заводе B₁ равна 100 единицам, то должно выполниться равенство

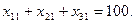
Аналогичные рассуждения привадят к равенствам

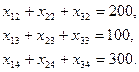
С другой стороны общее количество руды, отправляемой с месторождения A₁ выражается суммой

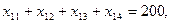
Аналогично получим

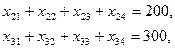
Таким образом, математическая формулировка транспортной задачи (по критерию стоимости перевозок) такова:

задана система семи линейных уравнений с двенадцатью неизвестными:

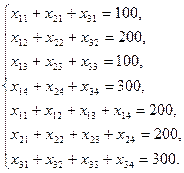
и линейная целевая функция F. (*).

Требуется среди всех неотрицательных решений x_ij данной системы выбрать такое, при котором функция F минимизируется, т.е.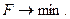

Пример5. Минимизация дисбаланса на линии сборки.

Фирма производит изделие, состоящее из трёх узлов. Эти узлы изготавливают на двух заводах. Производительность заводов по выпуску каждого из трёх видов узлов неодинакова. В таблице 7 указаны производительность заводов по выпуску каждого из узлов и суммарное время, которое каждый из заводов может выделить в течение недели на производство этих узлов.

Табл.7

Завод	Максимальный недельниый фонд, ч	Производительность, уз/ч
Узел 1	Узел 2	Узел 3

Требуется определить еженедельные затраты времени (в ч.) на производство каждого из трёх видов узлов на каждом заводе, обеспечивающие максимальный выпуск изделий.

Обозначим через x_ij недельный фонд времени (ч.), выделяемый на i-м заводе для производства j-го узла, i=1,2, j=1,2,3. Всего в задаче 6 переменных.

Определим, сколько узлов каждого вида поступит на линию сборки в течение недели.

Первый завод за неделю изготовит 8x₁₁ узлов первого вида, 4x₁₂ узлов второго вида, 6x₁₃ узлов третьего вида. Для второго завода эти числа равны соответственно 2x₂₁, 5x₂₂, 3x₂₃. Тогда на линию сборки поступит 8x₁₁+2x₂₁ узлов первого вида, 4x₁₂+5x₂₂ узлов второго вида, 6x₁₃+3x₂₃ узлов третьего вида. Число готовых изделий равно минимальному из этих трёх выражений. Это число требуется максимизировать.

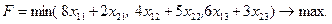
Время, затраченное каждым из заводов на производство всех трёх узлов, не должно превышать суммарного недельного фонда времени. Поэтому

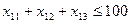(для первого завода)

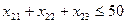(для второго завода).

Кроме того, 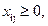i=1,2, j=1,2,3.

Построенная модель не линейна, так как не линейна целевая функция F. Целевую функцию можно сделать линейной, если положить .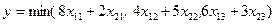

Тогда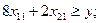

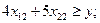
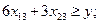
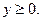
Окончательно математическую модель можно записать так 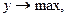при ограничениях

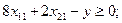
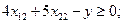
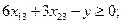
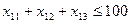
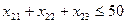
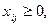i=1,2, j=1,2,3;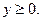

Тема 2. Графический метод решения задач линейного программирования.