Оценка погрешности по способу границ

Источники погрешности при решении задач на Э В М

Анализ погрешностей является неотъемлемой частью процесса решения прикладной задачи.

На общую погрешность задачи влияет целый ряд факторов. Отметим основные из них, рассмотрев общий ход решения задачи – от построения математической модели до производства вычислений.

Пусть R – точное значение результата решения некоторой задачи. Из-за несоответствия построенной математической модели реальной ситуации, а также по причине неточности исходных данных вместо R будет получен результат, который обозначим R1. Образовавшаяся таким образом погрешность ε1 = R – R1 уже не может быть устранена в ходе последующих вычислений (так называемая неустранимая погрешность).

Приступив к решению задачи в рамках математической модели, мы избираем приближенный (например, численный) метод и, еще не приступив к вычислениям, допускаем новую погрешность, приводящую к получению результата R2 (вместо R1). Погрешность ε2 = R2 – R1 называют погрешностью метода.

Действия над числами вносят дополнительную погрешность. Например, если складывать два числа с одинаковыми погрешностями, то погрешность суммы будет, вообще говоря, больше погрешности каждого из слагаемых. Это обстоятельство, а также неизбежность округлений (в случае использования ЭВМ принудительное округление диктуется конечностью разрядной сетки машины) приводят к получению результата R3, отличающегося от R2 на величину вычислительной погрешности ε3 = R3 – R2.

Полная погрешность ε, очевидно, получается как сумма всех погрешностей:

ε = R - R3 = (R – R1) + (R1 - R2) + (R2 – R3) = ε1 +ε2 +ε3.

При решении конкретных задач те или иные виды погрешностей могут отсутствовать или незначительно влиять на окончательный результат. Тем не менее, для исчерпывающего представления о точности окончательного результата в каждом случае необходим полный анализ погрешностей всех видов. Это в полной мере относится и к неустранимой погрешности – погрешности математической модели. Располагая несовершенной математической моделью, вычислитель должен каким-то способом составить представление о величине неустранимой погрешности. Понятно, что в условиях слишком грубой модели не имеет смысла проводить утонченный анализ вычислительных ошибок. Отсюда следует, что оценка неустранимой погрешности может послужить веским доводом для снижения требований к точности последующих вычислений, что, в свою очередь, может сделать их менее трудоемкими.

Основные понятия теории погрешностей

Пусть x – точное значение некоторой величины, a — наилучшее из известных приближений. В этом случае ошибка (или погрешность) приближения х определяется разностью x - a. Обычно знак этой ошибки не имеет решающего значения, поэтому рассматривают абсолютную величину ошибки:

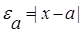
которую называют абсолютной погрешностьювеличины x. Кроме абсолютной погрешности часто используется относительная погрешность, которая определяется как отношение

= ,

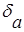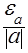Относительную погрешность обычно выражают в процентах. Приведённые выражения для e_a и d_a практически не могут быть использованы, так как истинное значение величины x неизвестно. Поэтому для оценки точности приближённых чисел находят предельную абсолютную погрешность Da, являющуюся верхней Da ³ 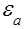оценкой | 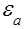|. Это значение определяется неоднозначно. Обычно стремятся указать число, наименьшее из возможных.

Если в приведённом выше выражении для относительной погрешности заменить абсолютную погрешность на предельную, то получим соотношение, определяющее предельную относительную погрешность.

=

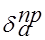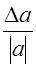
Говоря в дальнейшем о погрешности приближённых величин, будем иметь в виду их предельные погрешности, т.е. =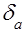

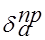
Если известны a и e_a, то принято записывать: x = a ± e_a. Это означает, что точное неизвестное значение х принадлежит промежутку от a – e_a до a + e_a.

Приближения к точному значению по недостатку и по избытку позволяет установить нижнюю и верхнюю границы.

Любая пара чисел НГ и ВГ такая, что 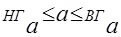называется соответственно нижнейи верхней границамиприближённой величины .

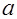Округление

В десятичной записи числа выделяют значащие цифры – это первая слева ненулевая цифра и любые цифры справа от значащей.

Пример.

В числе 3,14 – 3 значащие цифры, в числе 2,345*10^-2=0,02345 – 4 значащие цифры, в числе 308,7060 – 7 значащих цифр, в числе 2,5 *10⁶ – 2 значащих цифры.

Округлением числа называется замена его близким по величине, но с меньшим количеством значащих цифр.

Различают округление симметричное (к ближайшему), к большему (с избытком) и к меньшему (с недостатком).

ВГ можно округлить только с избытком, а НГ – с недостатком. Предельная погрешность является верхней границей погрешности и округляется с избытком.

Округление отбрасыванием цифр называется отсечением и широко применяется в ЭВМ ввиду простоты и быстроты выполнения.

Для приближённого числа, полученного в результате округления отсечением, абсолютная погрешность равна единице последнего разряда числа.

Пример. Округление отсечением числа х = 1,2759 до двух знаков после запятой а = 1,27 даёт абсолютную погрешность .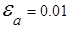

Симметричное округление приводит к меньшей величине ошибки округления. Его погрешность не превышает половины единицы последнего сохраняемого разряда.

Пример. Симметричное округление числа х = 1,2759 до двух знаков после запятой а = 1,28 даёт абсолютную погрешность .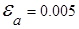

Введём понятия «верной цифры» и «верной цифры в строгом смысле», соответствующие двум рассмотренным способам округления.

Цифра, соответствующая р-му разряду в записи числа а, называется верной, если погрешность 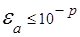, а если погрешность 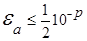, то цифра верна в строгом смысле. Цифра слева от верной также верна.

Пример. Пусть х=18,572 и известно, что 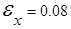. Сколько верных цифр в числе х ?

Имеем 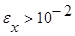, но 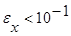. Значит в числе х верные цифры 1, 8, 5, а 7 и 2 – сомнительные. Верными в строгом смысле являются только цифры 1, 8, так как. .

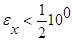Оценка погрешности по способу границ