Временные ряды. Методы сглаживания проявлений неопределенности
Часто при анализе используются ежегодные, ежемесячные и т.д. данные (особенно в макроэкономике). В этом случае данные упорядочивают по времени получения, т.е. строят временной ряд.
Для исследования явления необходимо значение показателя в текущий момент времени, в прошедшие моменты времени (и само время) и можно прогнозировать значения в будущем периоде. Такие модели называют динамическими.
Динамические модели подразделяют:
1. Модели с лагами – это модели содержащие в качестве лаговых переменных лишь независимые переменные, например
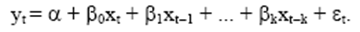
2. Авторегрессионные модели – это модели, уравнения которых в качестве лаговых объясняющих переменных включают значения зависимых переменных, пример
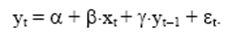
Основные задачи анализа временных рядов. Базисная цель статистического анализа временного ряда заключается в том, чтобы по имеющейся траектории этого ряда:
1) определить, какие из неслучайных функций присутствуют в разложении (3.1), т.е. определить значения индикаторов ci;
2) построить "хорошие" оценки для тех неслучайных функций, которые присутствуют в разложении (3.1);
3) подобрать модель, адекватно описывающую поведение случайных остатков et, и статистически оценить параметры этой модели;
4) прогнозирование значений временного ряда.
Первые три задачи относятся к общей задаче моделирования временного ряда, четвертая же обычно использует результаты такого моделирования.
Существуют две основные цели анализа временных рядов: (1) определение природы ряда и (2) прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям). Обе эти цели требуют, чтобы модель ряда была идентифицирована и, более или менее, формально описана. Как только модель определена, вы можете с ее помощью интерпретировать рассматриваемые данные (например, использовать в вашей теории для понимания сезонного изменения цен на товары, если занимаетесь экономикой). Не обращая внимания на глубину понимания и справедливость теории, вы можете экстраполировать затем ряд на основе найденной модели, т.е. предсказать его будущие значения.
Методы сглаживания временного ряда
1. Метод скользящего среднего определяется для каждого момента времени значение скользящей средней для этого находится среднее значение суммы текущего значения, предшествующего и последующего.
2. Экспоненциальное сглаживание производится по формуле St = a*Хt + (1-a)* St-1
3. Если временной ряд содержит ярко выраженную полиномиальную тенденцию (в виде полинома от t), то с целью устранения тенденции можно применить метод последовательных разностей, заключающийся в замене исходных уровней ряда последовательными разностями соответствующих порядков (порядок разности равен порядку полинома).
Если временной ряд содержит ярко выраженную линейную тенденцию, ее можно устранить путем замены исходных уровней ряда цепными абсолютными приростами - первыми последовательными разностями
Dyt = УХ - ум.
Если временной ряд содержит тенденцию в форме параболы второго порядка, то для ее устранения можно заменить исходные уровни ряда на вторые разности
Ay = Ay - Ayt-1.
Если тенденции временного ряда соответствует экспоненциальный или степенной тренд, метод последовательных разностей следует применять не к исходным уровням ряда, а к их логарифмам.
При всей своей простоте метод последовательных разностей имеет два су-щественных недостатка. Во-первых, его применение связано с сокращением числа пар наблюдений, по которым строится уравнение регрессии, и, следовательно, с потерей числа степеней свободы. Во-вторых, использование вместо исходных уровней временных рядов их приростов или ускорений приводит к потере информации, содержащейся в исходных данных.
