Розкриття невизначених виразів типу для алгебраїчних функцій
ЛЕКЦІЯ 14-15. Границя функції. Особливі границі функції
ПЛАН
1. Поняття границі функції
2. Зведення поняття границі функції до границі послідовності
3. Розкриття невизначених виразів типу 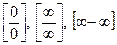 для алгебраїчних функцій
для алгебраїчних функцій
Поняття границі функції
Нехай функція 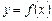 визначена у деякому околі точки х=а, за винятком, хіба що, самої точки х=а.
визначена у деякому околі точки х=а, за винятком, хіба що, самої точки х=а.
Означення. Число b називається границею функції 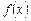 при
при 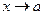 , якщо для будь-якого
, якщо для будь-якого 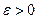 існує число
існує число 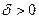 , таке що при
, таке що при 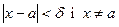 виконується нерівність
виконується нерівність 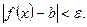
Коротко це означення можна записати так:
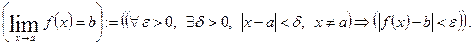
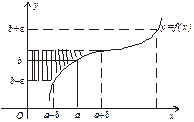 Рис. 1 Рис. 1 |
На рис. 1 показано геометричну інтерпретацію 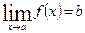 , де за заданим e-околом числа b знайдено d-окіл числа а такий, що для всіх
, де за заданим e-околом числа b знайдено d-окіл числа а такий, що для всіх 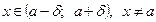 відповідні значення функції
відповідні значення функції 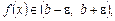 тобто графік функції
тобто графік функції 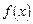 лежить у смузі шириною 2e.
лежить у смузі шириною 2e.
Нехай область визначення функції включає нескінченний проміжок.
Означення. Число b називається границею функції 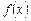 , коли
, коли  якщо для будь-якого
якщо для будь-якого 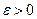 існує число
існує число 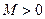 , таке що з нерівності
, таке що з нерівності 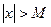 випливає нерівність
випливає нерівність 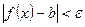 . Коротко це можна записати так:
. Коротко це можна записати так:
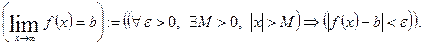
При 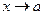 або
або 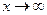 функція може набувати нескінченно великих значень чи прямувати до нуля. Ці випадки можна проілюструвати такими означеннями.
функція може набувати нескінченно великих значень чи прямувати до нуля. Ці випадки можна проілюструвати такими означеннями.
Означення. Функція 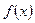 називається нескінченно великою величиною (н.в.в.) при
називається нескінченно великою величиною (н.в.в.) при 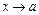 , якщо для будь-якого
, якщо для будь-якого 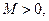 яке б велике воно не було, існує число
яке б велике воно не було, існує число 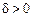 , таке що з нерівності
, таке що з нерівності 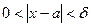 випливає
випливає 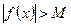 , тобто:
, тобто:
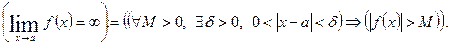
Означення. Функція 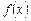 називається нескінченно малою величиною (н.м.в.) при
називається нескінченно малою величиною (н.м.в.) при 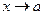 , якщо
, якщо 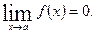
Розглянемо односторонні границі для функції 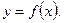
Означення. Правостороння границя функції:

Означення. Лівостороння границя функції:
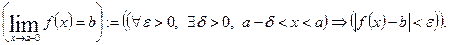
Теорема. Для існування 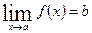 необхідно і достатньо, щоб виконувалась умова
необхідно і достатньо, щоб виконувалась умова 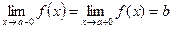
Зведення поняття границі функції до границі послідовності
Послідовність за означенням є функція, отже, границя послідовності - просто окремий випадок границі функції. Навпаки, у деякому розумінні границя функції може бути зведена до границі послідовності.
Нехай задано функцію 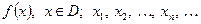 - послідовність значень аргументу функції з області D; цій послідовності відповідатиме така послідовність значень функції:
- послідовність значень аргументу функції з області D; цій послідовності відповідатиме така послідовність значень функції: 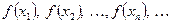 .
.
Означення. Число b називається границею функції 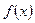 при
при 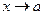 , якщо для будь-якої послідовності значень аргументу xn,
, якщо для будь-якої послідовності значень аргументу xn, 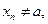 що має границею число а, відповідна послідовність значень функції
що має границею число а, відповідна послідовність значень функції 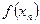 має границею число b.
має границею число b.
Відповідно до означення поняття границі функції фактично зведено до поняття границі послідовності, тому теореми про границі послідовностей також справджуються для границь функцій, тобто не потрібно формулювати ці теореми ще раз для границь функцій.
Розкриття невизначених виразів типу для алгебраїчних функцій
При виконанні граничного переходу у виразах типу 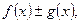
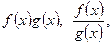 коли порушуються умови теореми про граничний перехід при арифметичних операціях, розв’язання задачі у ряді випадків зводиться до аналізу невизначених виразів виду
коли порушуються умови теореми про граничний перехід при арифметичних операціях, розв’язання задачі у ряді випадків зводиться до аналізу невизначених виразів виду 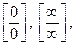

Розглянемо деякі загальні рекомендації щодо дослідження таких невизначених виразів, обмежуючись тільки алгебраїчними функціями.
