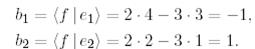Түйіндес кеңістіктің базисі
Анықтама 3. 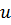 векторы және
векторы және 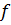 ковекторы бір-біріне ортогональ деп аталады, егер
ковекторы бір-біріне ортогональ деп аталады, егер 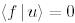 болса.
болса.
Айталық, 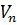 кеңістігінде
кеңістігінде 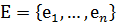 базисі берілсін.
базисі берілсін. 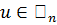 векторының Е базисі бойынша (2) – жіктелуіндегі
векторының Е базисі бойынша (2) – жіктелуіндегі 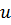 векторының
векторының 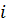 -шы координатын қарастырайық. (2) жіктелудің бірмәнділігінен
-шы координатын қарастырайық. (2) жіктелудің бірмәнділігінен 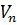 кеңістігінен бір бекітілген базисті таңдап алғанда
кеңістігінен бір бекітілген базисті таңдап алғанда 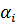 координаты – бұл сан,
координаты – бұл сан, 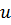 векторымен бірмәнді анықталады.
векторымен бірмәнді анықталады.
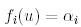 (8)
(8)
формуласымен анықталатын 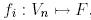 бейнелеуін қарастырайық.
бейнелеуін қарастырайық.
Векторларды қосқанда олардың координаты Е базисінде қосылады, ал векторды санға көбейткенде, оның координаттары осы санға көбейтіледі. Бұдан жоғарыда анықталған бейнелеу сызықты болады: 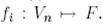 Ендеше,
Ендеше, 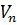 кеңістігінде әрбір
кеңістігінде әрбір 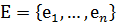 базисін таңдау
базисін таңдау 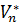 кеңістігінен алынған қандай да бір
кеңістігінен алынған қандай да бір 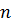 функционалдар жиынтығымен байланысады.
функционалдар жиынтығымен байланысады. 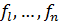 функционалдары
функционалдары 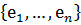 базисінің координаттық функционалдары деп атайды. Олар үшін
базисінің координаттық функционалдары деп атайды. Олар үшін
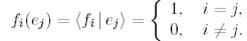 (9)
(9)
(9) қатынасты биортогональдық қатынасы деп, ал (9) қатынасты қанағатандыратын 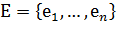 және
және 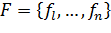 векторлар жүйесі биортогональды деп аталады, және
векторлар жүйесі биортогональды деп аталады, және 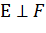 деп белгіленеді.
деп белгіленеді.
Теорема 1. 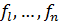 координаттық функционалдары сызықтық тәуелсіз және
координаттық функционалдары сызықтық тәуелсіз және 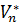 кеңістігінде базис құрайды.
кеңістігінде базис құрайды.
Дәлелдеу. 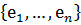 базисінде нөлге тең координаттық функционалдардың сызықтық комбинациясын қарастырайық:
базисінде нөлге тең координаттық функционалдардың сызықтық комбинациясын қарастырайық:
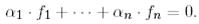 (10)
(10)
(10) сол жақ бөлігі нөлдік функционал болып табылады. Ендеше, оның мәні 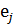 базистік векторында нөлге тең:
базистік векторында нөлге тең:
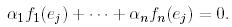 (11)
(11)
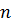 қосылғыштан тұратын (9) биортогональдық қатынастың негізінде (11) сол жақ бөлігінде тек қана
қосылғыштан тұратын (9) биортогональдық қатынастың негізінде (11) сол жақ бөлігінде тек қана 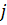 -ші қосылғыш қана қалады, сонымен қатар
-ші қосылғыш қана қалады, сонымен қатар 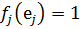 . Сондықтан да, (11)-ден
. Сондықтан да, (11)-ден 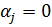 болады.
болады. 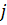 кез келген болғандықтан, енді (10) сызықтық комбинацияның тривиальдығы және
кез келген болғандықтан, енді (10) сызықтық комбинацияның тривиальдығы және 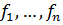 координаттық функционалдардың сызықтық тәуелсіздігі шығады.
координаттық функционалдардың сызықтық тәуелсіздігі шығады.
Теореманы дәлелдеуді аяқтау үшін кез келген 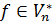 функционалы
функционалы 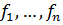 координаттық функционалдың сызықтық комбинациясына жіктелуі мүмкін.
координаттық функционалдың сызықтық комбинациясына жіктелуі мүмкін.
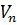 кеңістігінен кез келген
кеңістігінен кез келген 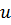 векторын қарастырайық. Онда (3) жіктеуден
векторын қарастырайық. Онда (3) жіктеуден 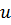 векторында
векторында 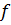 функционалының мәні үшін (8) ескеріп мынаны аламыз:
функционалының мәні үшін (8) ескеріп мынаны аламыз:
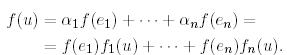 (12)
(12)
Мұнда 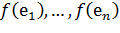 –
– 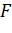 тан алынған сандар жиынтығы.
тан алынған сандар жиынтығы. 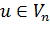 векторы кез келген болғандықтан алынған теңдікті функционалдар теңдігі ретінде жазуға болады:
векторы кез келген болғандықтан алынған теңдікті функционалдар теңдігі ретінде жазуға болады:
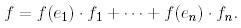 (13)
(13)
(13) формула кез келген 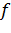 функционалын
функционалын 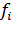 координаттық функционалдардың сызықтық комбинациясына жіктелуі болып табылады. Мұндай сызықтық комбинацияның коэффициенттері
координаттық функционалдардың сызықтық комбинациясына жіктелуі болып табылады. Мұндай сызықтық комбинацияның коэффициенттері 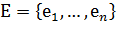 базистік векторында
базистік векторында 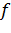 функционалының мәніне тең болады.
функционалының мәніне тең болады.
Салдар 1. 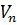 кеңістігінің кез келген Е базисі үшін
кеңістігінің кез келген Е базисі үшін 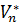 кеңістігіне тиісті,
кеңістігіне тиісті, 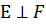 болатындай жалғыз ғана
болатындай жалғыз ғана 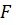 базисі бар болады.
базисі бар болады.
Анықтама 4. 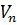 кеңістігінде
кеңістігінде 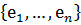 базисінің координаттық функционалдарынан құралған
базисінің координаттық функционалдарынан құралған 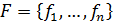 базисі Е үшін түйіндес базис деп аталады.
базисі Е үшін түйіндес базис деп аталады.
Мысал 1. (Биортогональды базистер). 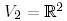 кеңістігін және оның базисін қарастырайық:
кеңістігін және оның базисін қарастырайық:
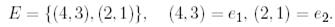
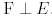 болатындай
болатындай 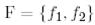 базисін табайық.
базисін табайық.
Кез келген 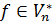 сызықтық функциясы
сызықтық функциясы
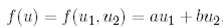
ережесі бойынша 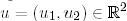 векторына әрекет етеді. (9) биортогональдық қатынасын қолданып,
векторына әрекет етеді. (9) биортогональдық қатынасын қолданып, 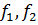 ізделінді функциялар үшін белгісіз
ізделінді функциялар үшін белгісіз 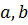 параметрлерін анықтайық.
параметрлерін анықтайық. 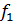 функциясы үшін бұл шарт мына түрге ие болады:
функциясы үшін бұл шарт мына түрге ие болады:
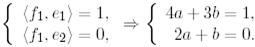
Дәл осылай 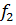 функциясы үшін бұл шарт мына түрге ие болады:
функциясы үшін бұл шарт мына түрге ие болады:
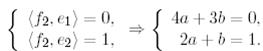
Бұл теңдеулер жүйесін шешейік:
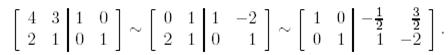
Табылған парметрлермен ізделінді функцияларды жазайық:
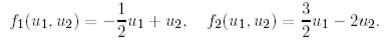
Осылайша, ізделінді базис 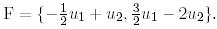
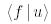 скаляр көбейтіндінің мәні биортогональды базисте басқа базистерге қарағанда жеңіл есептелетіндігін көрсетейік.
скаляр көбейтіндінің мәні биортогональды базисте басқа базистерге қарағанда жеңіл есептелетіндігін көрсетейік.
Айталық 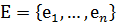 және
және 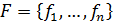 – сәйкесінше
– сәйкесінше 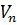 және
және 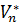 кеңістіктеріндегі екі кез келген базис болсын. Е базисіндегі жіктелуі (2) түрге ие болатын
кеңістіктеріндегі екі кез келген базис болсын. Е базисіндегі жіктелуі (2) түрге ие болатын 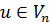 векторының скаляр көбейтіндісін және
векторының скаляр көбейтіндісін және 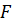 базисі бойынша жіктелген
базисі бойынша жіктелген 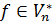 ковекторын қарастырайық:
ковекторын қарастырайық:
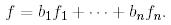 (14)
(14)
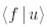 скаляр көбейтіндіні
скаляр көбейтіндіні 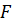 базисіндегі ковектордың және Е базисінде
базисіндегі ковектордың және Е базисінде 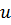 векторының координаты арқылы өрнектейік:
векторының координаты арқылы өрнектейік:
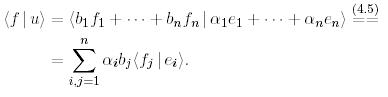 (15)
(15)
Егер 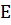 және
және 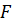 базистері биортогональ болса, яғни
базистері биортогональ болса, яғни 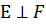 , онда (9) биортогональдық қатынасының негізінде (15) теңдік ықшамдалып мына түрге ие болады:
, онда (9) биортогональдық қатынасының негізінде (15) теңдік ықшамдалып мына түрге ие болады:
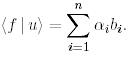
Осылайша,биортогональ базисте 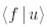 скаляр көбейтіндінің мәні оңай есептеледі.
скаляр көбейтіндінің мәні оңай есептеледі.
Биортогональ базисте вектордың және ковектордың координаттарын анықтайтын өрнекті табайық. Ол үшін мынаны есептейік:
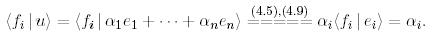
Ендеше,
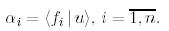 (16)
(16)
Ары қарай мынадай есептеу жүргізейік:
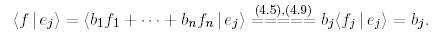
Онда,
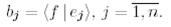 (17)
(17)
Мысал 2. (вектордың және ковектордың координаттары). Е базисінде 1-мысалдағы 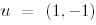 векторының координатын
векторының координатын 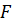 биортогональ базисін қолданып
биортогональ базисін қолданып 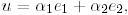 анықтайық. (16) сәйкес мынаны аламыз:
анықтайық. (16) сәйкес мынаны аламыз:
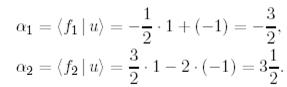
1-мысалдағы 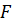 базисінде
базисінде 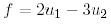 ковектордың координатын
ковектордың координатын 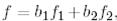 Е биортогональ базисін қолданып анықтайық. (17) сәйкес мынаны аламыз:
Е биортогональ базисін қолданып анықтайық. (17) сәйкес мынаны аламыз: