Геометрические построения в примере

Словесная форма	Графическая форма
1. Построить горизонталь (либо фронталь) в плоскости треугольника АВС: – провести фронтальную проекцию горизонтали h2; – построить h1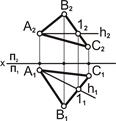
2. Выполнить первую замену плоскостей проекций П1П4 и преобразовать плоскость треугольника общего положения АВС в проецирующую: – провести ось x`– ось пересечения плоскостей проекций П1П4 перпендикулярно горизонтальной проекции горизонтали h1, построить проекцию треугольника АВС на плоскости П4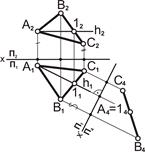

Окончание табл. 6.1

Словесная форма	Графическая форма
3. Выполнить вторую замену плоскостей проекций П4П5 и преобразовать проецирующую плоскость треугольника (АВС) в плоскость уровня: – провести ось x`` параллельно проекции А4В4С4); – от оси отложить расстояния удаления точек А, В, С до плоскости П4; – соединить полученные точки А5, В5, С5. Проекция А5В5С5 определяет натуральную величину |А5В5С5| = IABCI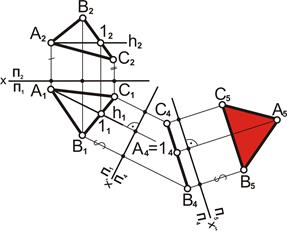

Метод вращения

Сущность этого способа заключается в том, что при неизменном положении основных плоскостей проекций изменяется положение заданных геометрических элементов относительно плоскостей проекций путем их вращения вокруг некоторой оси до тех пор, пока эти элементы не займут частное положение в исходной системе плоскостей.

В качестве осей вращения удобнее всего выбирать проецирующие прямые или прямые уровня, тогда точки будут вращаться в плоскостях, параллельных или перпендикулярных плоскостям проекций. Таким образом, различают следующие случаи метода вращения: метод вращения вокруг проецирующих прямых (проецирующей оси), метод плоскопараллельного перемещения (переноса), метод вращения вокруг прямых уровня.

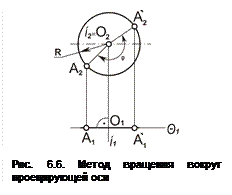Метод вращения вокруг проецирующей оси.Рассмотрим пример на рис. 6.6, где показано вращение точки на эпюре Монжа. Предположим, что точка А вращается вокруг оси i, перпендикулярно плоскости П₂ и описывает окружность с центром в точке О в плоскости Q, перпендикулярной оси i и параллельной плоскости П₂ (Q^i, QIIП₂).Траектория движения точки А будет проецироваться на плоскость П₂ в виде окружности радиуса R, а на плоскость П₁ – в виде отрезка длиной 2R. Если точку А повернуть против часовой стрелки на угол j в новое положение А`, то фронтальная проекция A`₂ повернется на тот же угол и попадает в точку A`₁.

В процессе решения задач методом вращения вокруг проецирующих осей этапы преобразования геометрических элементов аналогичны тем, которые выполняются методом замены плоскостей проекций.

пример. Дана плоскость общего положения Σ(ΔABC). Методом вращения вокруг проецирующей прямой определить натуральную величину треугольника АВС (табл. 6.2).

Таблица 6.2