Результаты численного эксперимента.
Модифицированный метод Эйлера.
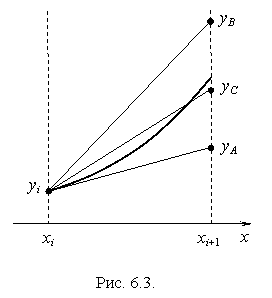
Рис2
Запишем уравнение прямой выходящей из точки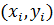 
с наклоном, равным наклону интегральной кривой в середине отрезка точки 
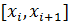(на рис.2). этой прямой соответствует прямая, проходящая через точк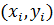и и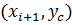 
):
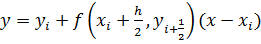
Для точки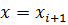 
получаем
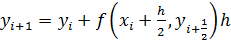
откуда немедленно следует разностное соотношение:
(*)
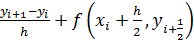Значение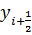 
, относящееся к середине отрезка 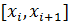, приближенно можно вычислить по методу Эйлера 
(**)
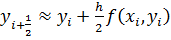Исключая из (*) промежуточные значения 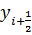(подстановкой выражения (**)), можно записать этот метод в виде следующей разностной схемы:
(***)
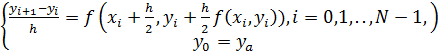Система уравнений (***) представляет собой явную одношаговую разностную схему, аппроксимирующую исходную задачу (1) со вторым порядком точности
Результаты численного эксперимента.
Введем N=4 и посмотрим, как ведут себя графики решений ОДУ y(t) и z(t). Использование модифицировынного метода Эйлера позволяет получить лучшую точность решения (меньшую погрешность), чем у явногеявного методов эйлера, несмотря на то что они имеют один и тот же порядок точности.
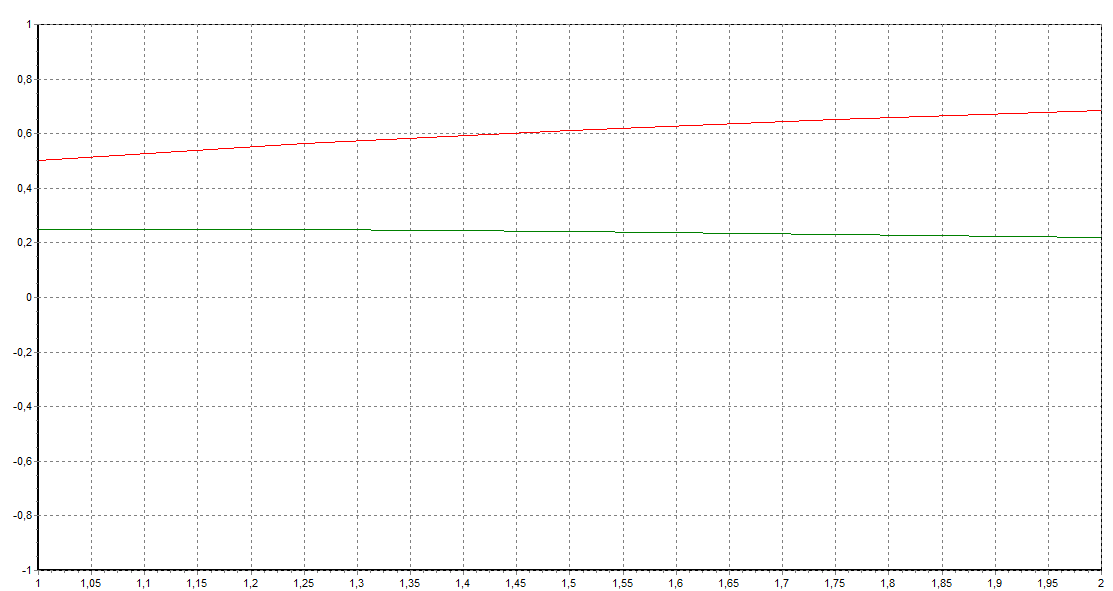при N=4
.
при N=25
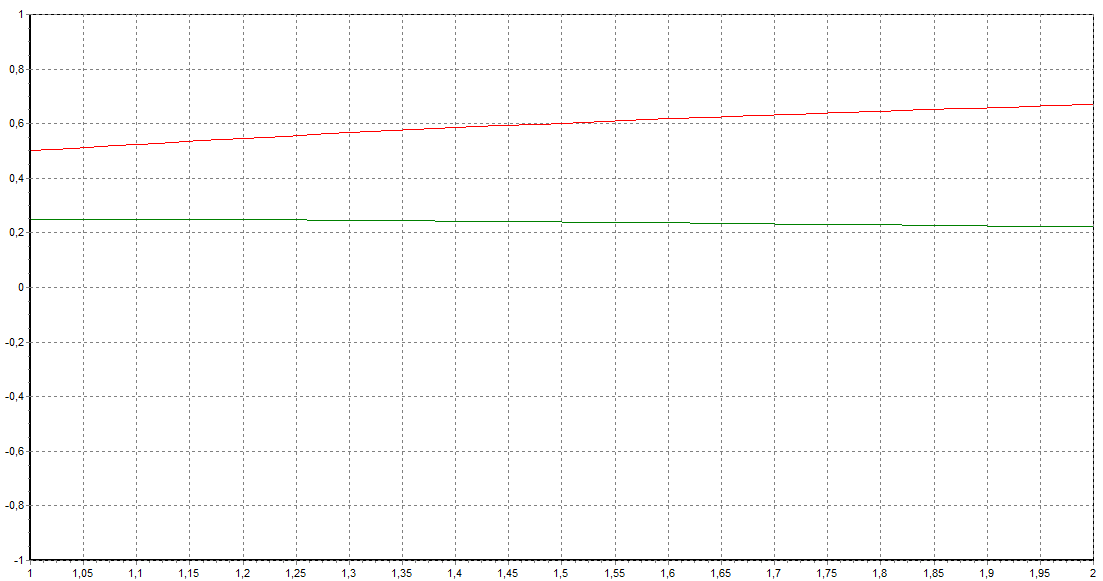
при N=1000
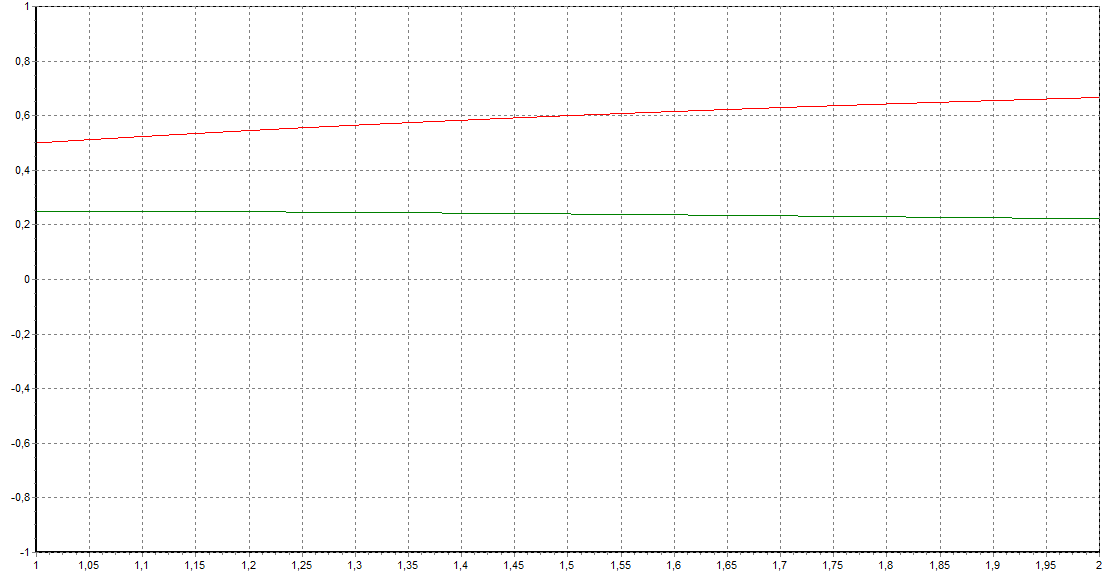
Вывод: С использованием Модифицированного методоа Эйлера найдено приближенное решение задачи Коши для системы обыкновенных дифференциальных уравнений.. Рассмотрение различных случаев привело к выводу, что использование Модифицированного метода Эйлера позволяет получить лучшую точность решения (меньшую погрешность), чем у явногои неявного метода , так как они имеют один и тот же порядок точности. При увеличении N погрешность вычислений становится меньше. Тем самым при больших значениях данного параметра график функции, построенный с помощью Модифицированного методоа Эйлера будут приближаться к графику самого решения.
Листинг программы на языке Delphi:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ComCtrls, TeEngine, Series, ExtCtrls, TeeProcs, Chart, Buttons, Functions;
type
TForm1 = class(TForm)
;
grp1: TGroupBox; edt_ modified_metod_y: TEdit; lbl1: TLabel; edt_ modified _metod_z: TEdit;
lbl2: TLabel; edt_ modified _meyod_y0: TEdit; lbl3: TLabel; edt_ modified _metod_z0: TEdit;
lbl4: TLabel; grp2: TGroupBox; cht_ modified _metod: TChart; lnsrs_ modified _metod_y: TLineSeries;
lnsrs_ modified _metod_z: TLineSeries; cht_ modified _metod: TChart; lnsrs_ modified _metod_y: TLineSeries;
lnsrs_ modified _metod_z: TLineSeries; Label6: TLabel;
procedure btn_ modified _metod_closeClick(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure btn_ modified _metod_solveClick(Sender: TObject);
procedure btn_ modified _metod_solveClick(Sender: TObject);
procedure btn_ modified _metod_grafikClick(Sender: TObject);
procedure GrafikTochn(l1,l2:Tlineseries);
procedure btn_ modified _metod_grafikClick(Sender: TObject);
procedure btn_ modified _metod_RungeClick(Sender: TObject);
procedure btn_ modified _metod_RungeClick(Sender: TObject);
end;
const hx=0.00001;
var
Form1: TForm1;
implementation
procedure TForm1.btn_ modified _metod_solveClick(Sender: TObject);
var h, xi, yi, zi:Real;
i,j:Integer;
begin
if input(edt_ modified _metod_y, edt_ modified _metod_z, edt_ modified _meyod_y0, edt_ modified _metod_z0, edt_ modified _metod_a, edt_ modified _metod_b, edt_ modified _metod_n, edt_ modified _metod_n) then
begin
lnsrs_ modified _metod_y.Clear; lnsrs_ modified _metod_z.Clear;
h:=(b-a)/n; yi:=y0; zi:=z0; xi:=a;
lnsrs_yavniy_ modified _y.AddXY(xi,yi); lnsrs_ modified _metod_z.AddXY(xi,zi);
for i := 0 to n-1 do
begin
FuncInput(y,xi,yi,zi); FuncInput(z,xi,yi,zi);
yi:=yi+h*y.FuncCount; zi:=zi+h*z.FuncCount; xi:=xi+h;
lnsrs_ modified _metod_y.AddXY(xi,yi); lnsrs_ modified _metod_z.AddXY(xi,zi);
end;
end;
end;
procedure TForm1.btn_ modified _metod_Click(Sender: TObject);
var h, h2, xi, yi, zi, yi2, zi2, e2:Real;
i,k:Integer; flag:Boolean;
begin
if input(edt_ modified _metod_y, edt_ modified _metod_z, edt_ modified _metod_y0, edt_ modified _metod_z0, edt_ modified _metod_a, edt_ modified _metod_b, edt_v_metod_e, edt_ modified _metod_n) then
begin
e2:=StrToFloat(edt_neyavniy_metod_e2.Text);
h2:=(b-a)/n; flag:=True; k:=n;
while flag do
begin
k:=k*2; yi:=y0; yi2:=y0; zi:=z0; zi2:=z0; h:=h2; h2:=h/2; xi:=a;
while xi<b do
begin
xi:=xi+h
end; xi:=a;
while xi<b do
begin
xi:=xi+h2;
flag:=((Abs(yi2-yi)>=e2)or(Abs(zi2-zi)>=e2)) end;
edt_neyavniy_metod_h.Text:=FloatToStr(h2);
edt_neyavniy_metod_Nr.Text:=IntToStr(Trunc((b-a)/h2)+1); end;
end;
procedure TForm1.GrafikTochn(l1,l2:Tlineseries);
var h, xi, yi, zi:Real; i,j:Integer;
begin
l1.Clear; l2.Clear; h:=(b-a)/200; xi:=a;
for i := 0 to 200 do
begin
yi:=Exp(xi);//2.5*(xi+0.8)-1.25*(xi+0.8)*(xi+0.8)-0.2;
zi:=xi+exp(xi);//0.2+5/4*(xi+0.8)*(xi+0.8);
l1.AddXY(xi,yi); l2.AddXY(xi,zi); xi:=xi+h; end;
end;
procedure TForm1.btn_ modified _metod_Click(Sender: TObject);
var h, h2, xi, yi, zi, yi2, zi2:Real; i,k:Integer; flag:Boolean;
begin
if input(edt_ modified _metod_y, edt_ modified _metod_z, edt_ modified _meyod_y0, edt_v_metod_z0, edt_ modified _metod_a, edt_ modified _metod_b, edt_ modified _metod_e2, edt_ modified _metod_n) then
begin
h2:=(b-a)/n; flag:=True; k:=n;
while flag do
begin
k:=k*2; yi:=y0; yi2:=y0; zi:=z0; zi2:=z0; xi:=a; h:=h2;h2:=h/2;
while xi<b do
begin
FuncInput(y,xi,yi,zi);FuncInput(z,xi,yi,zi); yi:=yi+h*y.FuncCount;
zi:=zi+h*z.FuncCount; xi:=xi+h;
end; xi:=a;
while xi<b do
begin
FuncInput(y,xi,yi2,zi2); FuncInput(z,xi,yi2,zi2);
yi2:=yi+h2*y.FuncCount; zi2:=zi+h2*z.FuncCount; xi:=xi+h2;
end;
flag:=((Abs(yi2-yi)>=e)or(Abs(zi2-zi)>=e)) end;
edt_ modified _metod_h.Text:=FloatToStr(h2);
edt_yav modified niy_metod_Nr.Text:=IntToStr(Trunc((b-a)/h2)+1);
end;
end.
Литература
1) Лекциии
2) http://physics.herzen.spb.ru/library/01/01/nm_labs/odeq.htm