Метод исключения (метод Гаусса)
Это – один из наиболее известных и широко применяемых прямых методов решения систем линейных уравнений.
Для иллюстрации метода рассмотрим уже знакомую нам систему из 3-х уравнений с тремя неизвестными:
а11х1 + а12х2 + а13х3 = b1 ; (3.1)
а21х1 + а22х2 + а23х3 = b2 ; (3.2)
а31х1 + а32х2 + а33х3 = b3 . (3.3)
В такой системе по крайней мере один из коэффициентов а11, а21, а31 должен быть отличен от нуля, иначе мы имели бы дело в этих 3-х уравнениях только с двумя неизвестными. Если а11 = 0, то можно переставить уравнения так, чтобы коэффициент при х1 в первом уравнении был отличен от нуля. Очевидно, что перестановка уравнений оставляет систему неизменной; ее решение остается прежним.
Теперь введем множитель:
.
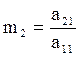Умножим (3.1) на m2, полученный результат вычтем из (3.2).
Результат вычитания:
(а21 - m2×a11)×x1 + (a22 - m2×a21)x2 + (a23 - m2×a13)x3 = b2 - m2×b1.
Но
а21 - m2×a11 = a21 -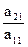 
×a11 = 0
Поэтому х1 исключено из уравнения (3.2).
Обозначим новые коэффициенты:
a'22 = a22 - m2×a12
a'23 = a23 - m2×a13
b'2 = b2 - m2×b1
Тогда (3.2) приобретет вид:
a'22×x2 + a'23×x3 = b'2 (3.2')
Заменим в системе уравнение (3.2) уравнением (3.2') и введем множитель для третьего уравнения:
.
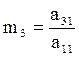Умножим (3.1) на m3, полученный результат вычтем из (3.3).
Коэффициент при х1 снова становится нулевым, и (3.3) приобретает вид:
a'32×x2 + a'33×x3 = b'3, (3.3')
где
a'32 = a32 - m3×a12
a'33 = a33 - m3×a13
b'3 = b3 - m3×b1.
Если теперь в исходной системе уравнений заменить (3.3) на (3.3'), то новая система выглядит так:
а11х1 + а12х2 + а13х3 = b1; (3.1)
а'22х2 + а'23х3 = b'2; (3.2')
а'32х2 + а'33х3 = b'3. (3.3')
Эти уравнения полностью эквивалентны исходным с тем преимуществом, что х1 входит только в уравнение (3.1). Уравнения (3.2') и (3.3') представляют систему из двух уравнений с двумя неизвестными. Если определить из нее х2 и х3, подставить их в уравнение (3.1), то можно определить х1.
Теперь исключим х2 из (3.2') и (3.3').
Для этого введем множитель:
.
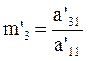Умножим (3.2') на m'3 и вычтем полученное из (3.3'). Получим:
(а'32 - m'3×a'22)×x2 + (a'33 - m'3×a'23)x3 = b'3 - m'3×b'2.
Но
(а'32 - m'3×a'22) = 0.
Полагая
a''33 = a'33 - m'3×a'23;
b''3 = b'3 - m'3×b'2 ,
окончательно получим:
a''33×x3 = b''3. (3.3'')
Уравнение (3.3') можно заменить уравнением (3.3"), после чего система уравнений приобретет следующий вид:
а11х1 + а12х2 + а13х3 = b1; (3.1)
а'22х2 + а'23х3 = b'2; (3.2')
а''33х3 = b''3. (3.3")
Такая система уравнений иногда называется треугольной из-за своего внешнего вида.
Теперь необходимо определить х3 из (3.3"), подставить его в (3.2'), определить х2, подставить х3 и х2 в (3.1) и найти х1. Этот процесс, который обычно называется обратной подстановкой, определяется формулами:
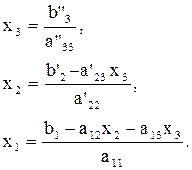
Вспомним, что мы переставили уравнения таким образом, чтобы а11 и а'22 не были равны нулю. Если окажется, что а"33 = 0, то система уравнений является вырожденной.
Все прямые методы сводятся к преобразованию матрицы к более простому виду (например, диагональный, треугольный).