Оптимизационные задачи для выпуклых функций

Общим недостатком рассмотренных выше методов безусловной оптимизации было, с одной стороны, то, что они позволяют отыскивать только точки возможного локального экстремума, а с другой - то, что найденные решения могут существенно зависеть от начального приближения. Поиск глобального оптимума подразумевает перебор найденных точек, который, в случае градиентных методов, может быть осуществлен за счет подбора соответствующих начальных приближений .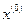

Рис. 2.1

Рис. 2.2

Однако существует один класс функций, для которых градиентные методы приводят к нахождению глобального оптимума. Это выпуклые функции.

Определение. Функция 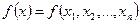называется выпуклойв области D, если для любых двух точек 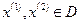и любого 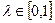выполняется неравенство

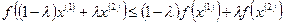(14)

если же

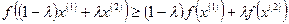(15)

то функция называется вогнутой.

Геометрический смысл понятий выпуклости и вогнутости для случая функции одной переменной представлен на Рис. 2.3. Из него, в частности, видно, что график выпуклой функции лежит ниже отрезка, соединяющего точк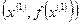и и 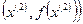, а график вогнутой - выше этого отрезка.

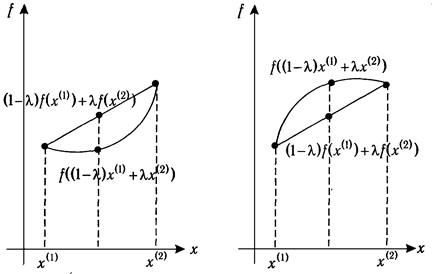
Рис. 2.3

Можно доказать, что достаточным условием выпуклости функции 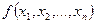является положительная определенность матрицы

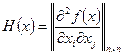
называемой также матрицей Гессе, во всех точках 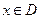. Соответственно, достаточным условием вогнутости является отрицательная определенность матрицы Гессе. В частности, для функций одной переменной достаточным условием выпуклости (вогнутости) является выполнение неравенства .

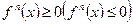Как следует из геометрической интерпретации, для выпуклой функции локальный экстремум, если он существует, совпадает с глобальным. Справедлива теорема.

Теорема 2.2. Если 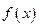выпуклая (вогнутая) на 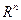функция и 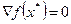, то 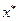- точка глобального минимума (максимума)

Доказательство.Доказательство достаточно провести для случая вогнутой функции, т. к. для противоположного случая оно будет аналогичным с точностью до знака.

Пусть 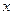- произвольная точка, отличная от точки 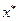. Тогда, для любого 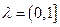, в силу вогнутости функции 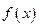выполнятся неравенство

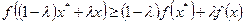
откуда следует

.

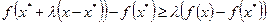Если ввести вектор 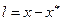и обозначить 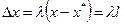, то длина вектора 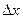будет равна 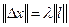. Следовательно,

.

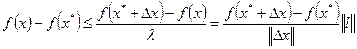Устремляя 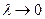и учитывая, что вектор l сонаправлен с 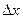, получим

.

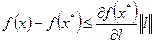По условию теоремы 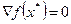. Это означает, что для любого вектора l (а, следовательно, для любой точки х) согласно формулы, выражающей производную по направлению через градиент, находим

.

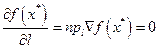Следовательно, для любой точки х отличной от 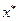, справедливо неравенство 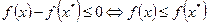, т.е. 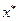- точка глобального максимума.

Поскольку выпуклые функции обладают столь «полезными» оптимизационными качествами, они занимают исключительно важное место в теории исследования операций. Соответствующий раздел математического программирования получил название выпуклого программирования, а общая задача выпуклого программирования формулируется как проблема поиска максимума вогнутой (минимума выпуклой) функции на выпуклом множестве.