Основные показатели среднего уровня вариационного ряда

Среднее арифметическое

Среднее арифметическое взвешенное для вариационного ряда определяется по формуле (3.1):

.

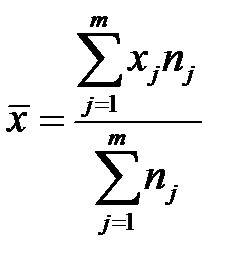Среднее арифметическое простое определяется по формуле (3.2):

.

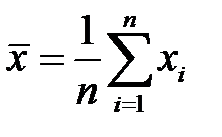Как мы видим, выборочное среднее, рассмотренное выше в п.3.1, вычисляется как среднее арифметическое.

Среднее гармоническое

Среднее гармоническое простое вычисляется по формуле

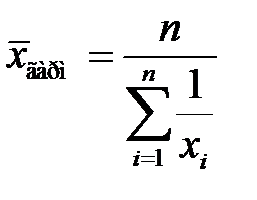. (3.16)

Среднее гармоническое взвешенное вычисляется по формуле

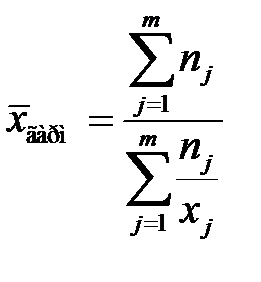. (3.17)

Пример 3.5. Пусть известны затраты времени каждого из десяти рабочих на производство одной детали в часах (Табл.3.2). Найти среднее значение затраты времени на одну деталь.

Таблица 3.2

№ рабочего
Затраты времени, час.	0,15	0,20	0,25	0,18	0,18	0,25	0,15	0,18	0,20	0,18

Решение. Среднее значение затраты времени на одну деталь равно общему количеству времени, деленному на количество деталей. Предположим, что каждый рабочий работал по одному часу, тогда общее количество времени равно 10, а число деталей, производимых одним рабочим, равно обратной величине затрат времени на одну деталь. Мы получаем, что среднее значение затраты времени на одну деталь равно среднему гармоническому затрат времени (3.16).

Введите данные из табл.3.2 в программе Excel, как показано на рис.3.4.

Рис.3.4

В ячейку В3 введите формулу =СРГАРМ(B2:K2). Получим 0,19.

Сгруппируйте данные из таблицы 3.2, т.е. запишите в виде вариационного ряда в диапазоне А5:Е7, как показано на рис.3.5.

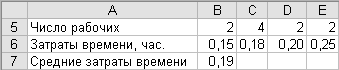
Рис.3.5

Теперь нужно применить среднее геометрическое взвешенное, т.е. формулу (3.17). В ячейку В7 введите формулу

=10/(B5/B6+C5/C6+D5/D6+E5/E6)

Полученное значение 0,19 совпадает с предыдущим, что подтверждает правильность вычислений.

Среднее геометрическое

Среднее геометрическое простое

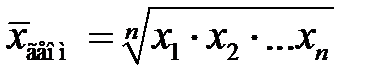. (3.18)

Среднее геометрическое взвешенное

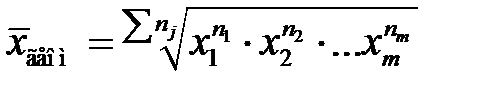. (3.19)

Применение среднего геометрического для определения среднего темпа роста будет показано в последней главе.

Мода

Мода — это такое значение во множестве наблюдений, которое встречается наиболее часто. Для дискретного ряда это значение с наибольшей частотой.

В программе Excel для вычисления моды дискретного набора применяется функция МОДА().

Пример 3.6. Найти моду дискретного ряда

1; 0; 6; 2; 4; 4; 1; 3; 4; 5; 6; 7; 2; 5; 4; 1; 2; 0; 0; 6.

Решение. Введите данные в диапазоне А1:А20. Введите в ячейку С1 формулу =МОДА(A1:A20). Получим число 4.

Замечание. Если ряд не содержит одинаковых данных, то функция МОДА() возвращает значение ошибки «#Н/Д».

Для интервального ряда с равными интервалами мода определяется по следующему алгоритму:

1) определяется модальный интервал (x_k–1, x_k), которому соответствует наибольшая частота n_k (или частость w_k);

2) значение моды вычисляется по интерполяционной формуле

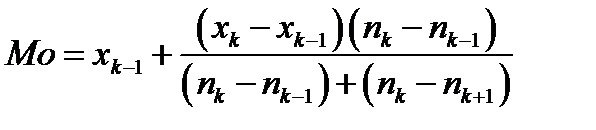. (3.20)

В случае интервального ряда с неравными интервалами мода определяется по наибольшей плотности частоты:

1) определяется модальный интервал (x_k–1, x_k), которому соответствует наибольшая плотность частот ;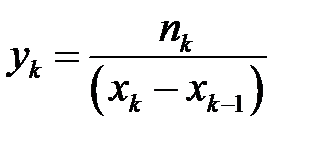

2) значение моды вычисляется по интерполяционной формуле

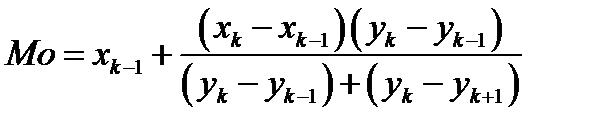. (3.21)

Пример 3.7. Найти моду для вариационного ряда, который показывает распределение предприятий региона по численности работников (табл.3.3).

Таблица 3.3

№ интервала
Число работников	1 – 10	11– 30	31 – 60	61 – 100	101 – 150	151 – 200	201 – 500
Число предприятий

Решение. Введите данные в программе Excel в диапазоне А1:D9, как показано на рис.3.6.

В ячейку Е3 введите формулу =C3-B3, в ячейку F3 введите =D3/E3. Выделите ячейки E3:F3, и протяните маркером заполенения вниз до F9.

Мы увидим, что наибольшая частота 60 соответствует третьему интервалу (31–60) с номером 3. Однако наибольшая плотность частоты 2,60 соответствует второму интервалу.

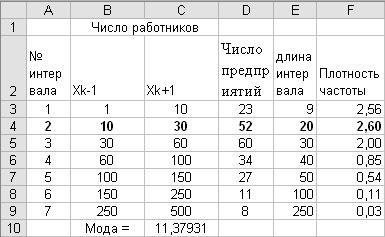
Рис.3.6

Применим для вычисления моды формулу (3.21).

В ячейку С10 введите формулу

=B4+E4*(F4-F3)/(F4-F3+F4-F5).

Получим значение моды 11,37931.

Медиана

Медиана — это такое значение признака, которое делит ранжированный ряд на две равные части.

Для дискретного вариационного ряда значение медианы определяется по формуле

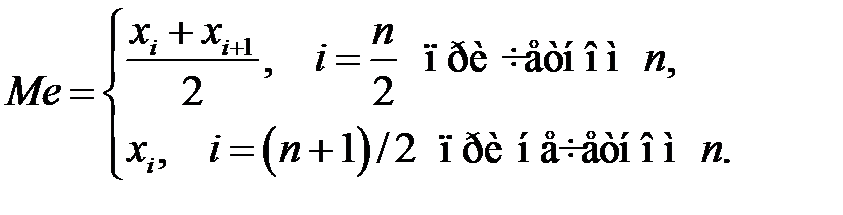(3.21)

Для простоты расчетов на практике для дискретного вариационного ряда номер медианы определяется по формуле

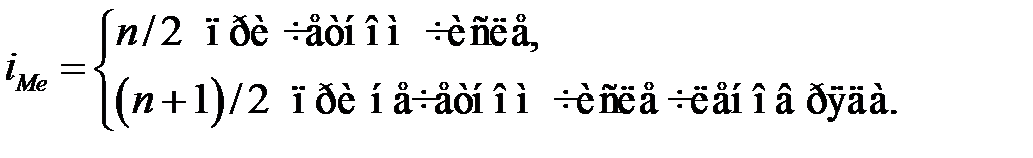(3.22)

В программе Excel для вычисления медианы дискретного вариационного ряда можно применить функцию МЕДИАНА().

Пример 3.8. Найти медиану дискретного ряда

1; 0; 6; 2; 4; 4; 1; 3; 4; 5; 6; 7; 2; 5; 4; 1; 2; 0; 0; 6.

Решение. Введите данные в диапазоне А1:А20. Введите в ячейку С1 одну из формул

=МЕДИАНА(A1:A20)

=ПЕРСЕНТИЛЬ(A1:A20;50%)

Получим значение 3,5. (Функция ПЕРСЕНТИЛЬ() рассматривается в следующем пункте.)

Проверим этот результат.

Выделите диапазон А1:А20 и с помощью команды меню «Данные — Сортировка» ранжируйте ряд по возрастанию. Так как число членов четное, то значение медианы вычисляем по формуле (3.21), т.е. как полусумму десятого и одиннадцатого значений. Получим (3 + 4)/2 = 3,5.

Для интервального вариационного ряда сначала определяют номер медианы как полусумму частот 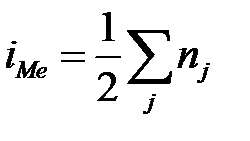. Затем отсчитывают накопленные частоты, и находят первый интервал (x_k–1, x_k), для которого сумма накопленных частот F_k не меньше номера медианы 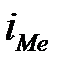. Медиана определяется с помощью интерполяционной формулы

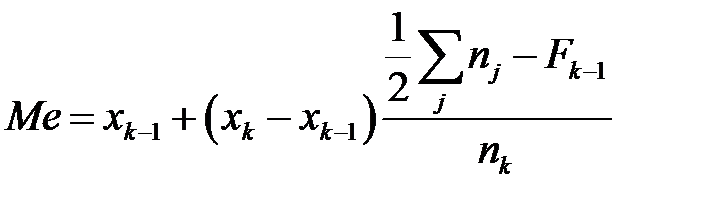. (3.23)

Пример 3.9.Найти медиану для вариационного ряда из примера 3.7.

Решение. Введите исходные данные из табл.3.3 примера 3.7 в диапазоне А1:D9, как показано на рис.3.7.

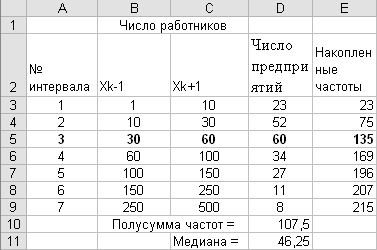
Рис.3.7

В ячейку D10 введите формулу =СУММ(D3:D9)/2.

В ячейку Е3 введем формулу =D3, а в ячейку Е4 — формулу =E3+D4.

Затем ячейку Е4 протяните маркером заполнения вниз до Е9.

Мы увидим, что медианным интервалом является интервал №3. Теперь применяем формулу (3.23). Для этого введите в ячейку D11 формулу

=B5+(C5-B5)*(D10-E4)/D5.

Получим значение медианы Me = 46,25.