II. Графическое представление результатов измерений

В ряде случаев для большей наглядности, экспериментальные данные целесообразно представлять графически в виде точек или линий. Такие графики позволяют быстро распознать характер исследуемых зависимостей, а в ряде случаев позволяют даже установить вид исследуемых зависимостей.

Приведем общие рекомендации для построения графиков.

1.Для графиков используется миллиметровая бумага с линейным масштабом.

2. Масштаб для построения графиков выбирается исходя из следующих соображений:

а) экспериментальные точки не должны сливаться

б) графики, близкие к прямым линиях, должны располагаться, примерно, под углом

45 градусов к осям координат

в) следует использовать либо десятичный масштаб (0,1; 1;10;100 и т.д. единиц

измеряемой величины в 1 см.), либо масштабы 2:1 или 5:1.

г) начало координат (X = 0 ,Y= 0) не обязательно должно присутствовать на графике.

д) снизу или справа от оси абсцисс, слева или сверху от оси ординат следует указать

название или (и) обозначение физической величины и через запятую- единицу

измерения, относя сюда и возможный десятичный множитель. Благодаря последнему,

масштабные деления на осях помечаются, как правило, не более чем трехзначными

числами.

3. При построении графиков следует придерживаться следующих правил:

а) первоначальную разметку масштаба и нанесение экспериментальных точек выполнять

мягким карандашом и лишь окончательно чернилами.

б) если на одном графике необходимо сравнить несколько экспериментальных

зависимостей, то следует пользоваться разными обозначениями для точек,

относящихся к разным величинам (например, 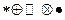и т.д.) можно использовать так

же разные цвета.

в) при сравнении экспериментальной и теоретической зависимостей теоретическую

кривую следует построить по произвольно выбранным точкам, а экспериментальную

кривую лучше не строить, указать отрезками при каждой точке величины

погрешностей.

г) не соединять экспериментальные точки ломаной линией. Наилучшую плавную кривую

следует провести с помощью лекал.

д) наиболее удобны для зрительного восприятия прямолинейные графики. Поэтому, если

есть возможность, следует преобразовать исследуемую зависимость в линейную и

изображать на графике зависимость между теми величинами, между которыми связь

линейная. Например, экспоненциальные зависимости 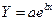или логарифмические

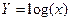удобно представлять в полулогарифмических координатах, а степенные -

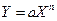в логарифмических координатах.

Необходимо хорошо представлять себе, что физические формулы записываются не для физических величин, а для их численных значений. Другими словами, эти формулы представляют собой численные равенства.

Согласно Международному стандарту ИСО 31/0 (Общее положение к ИСО 31), аргументами показательных и логарифмических функций должны быть или безразмерные величины или числовые значения величин.

В качестве примера, рассмотрим представление экспериментальных данных, полученных в результате исследования зависимости вязкости крови от показателя гематокрита (данные взяты из монографии «Механика кровообращения» авт. К. Каро,

Т. Педли д.р.)

Показатель гематокрита, H	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
Вязкость крови, η [Па*с]	0,028	0,080	0,229	0,653	1,867	5,336	15,250	43,579
Ln{η}	-3,58	-2,53	-1,48	-0,43	0,63	1,68	2,73	3,78

По оси абсцисс откладываем показатель гематокрита H, а по оси ординат соответствующую этим значениям вязкость крови.

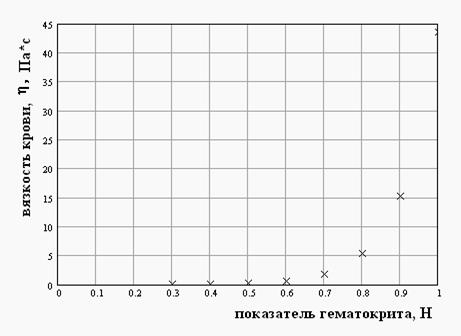
Нанесенные точки указывают на криволинейную зависимость. График получается очень не наглядным, и сделать какие либо предположения о характере зависимости практически невозможно

Добавим нашу таблицу строкой Ln{η} и перестроим график в полулогарифмических координатах, откладывая по оси ординат не вязкость, а численное значение логарифма вязкости.

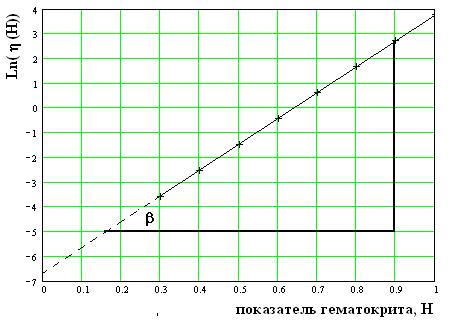
Экспериментальные точки теперь хорошо укладываются на прямую линию, что дает возможность предположить о наличии экспоненциальной зависимости коэффициента вязкости от показателя гематокрита.

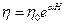η = η₀ exp(αH).

Более того, по графику, экстраполируя прямую до пересечения с осью ординат можно определить вязкость при нулевом гематокрите, т.е. вязкость плазмы крови: η₀ = 0,0012 Па_*с Тангенс угла наклона прямой дает возможность определить показатель степени экспоненты

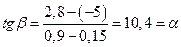
Окончательно имеем:

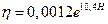, Па_*с η = 0,0012 exp(10,4H),Па_*с

Пример 6

В той же монографии представлены данные зависимости коэффициента вязкости крови η от скорости сдвига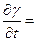

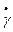
Скорость сдвига, 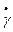[1/c]	0.2	0.5
Коэффициент вязкости, η [Па*с]	57.7	38.3	27.4	14.	10.1		3.7
Ln { 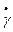}	-1.609	-0.693		1.609	2.303	3.912	4.605	6.215
Ln {η}	4.055	3.645	3.311	2.639	2.313	1.609	1.308	0.693

Представим экспериментально полученные данные на графике

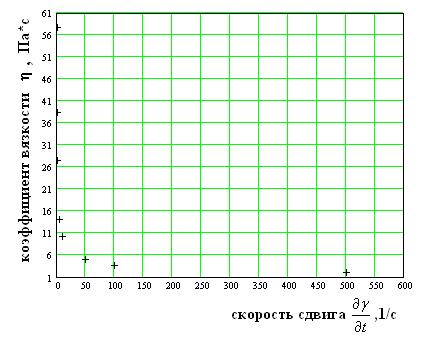
Опять получаем очень не наглядный график, и сделать какие либо предположения о характере зависимости практически невозможно.

Перестроим график в полулогарифмических координатах: η; Ln { }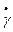

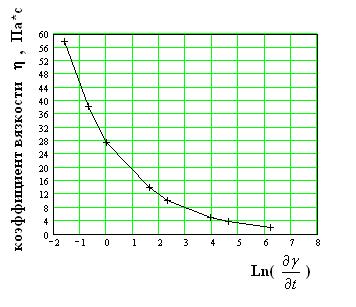
График становится более наглядным, однако сказать что- либо определенное о характере зависимости невозможно.

Перестоим график в логарифмических координатах Ln {η}; Ln { }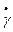

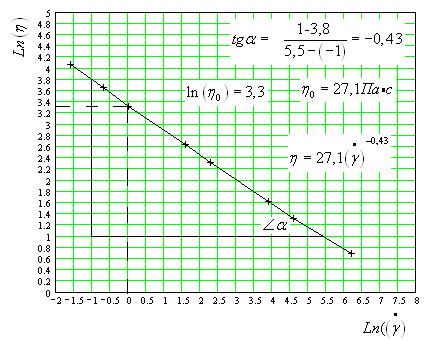
Точки хорошо укладываются на прямую линию. Полученная линейная зависимость позволят предположить о степенной зависимости вязкости η от скорости сдвига .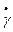

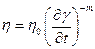
Определяя из графика η₀ = 27,1 [Па_*с] и m = tg α = - 0,43

Окончательно получим:

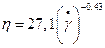, Па_*с

III. Метод наименьших квадратов.

Очень часто, несмотря на просматриваемый линейный характер исследуемой зависимости, экспериментальные точки не укладываются на прямую, имея значительный разброс.

В этом случае, для обработки результатов экспериментальных данных применяют метод наименьших квадратов.

1.Предполагается, что величины х и y связаны линейной зависимостью.

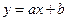
однако коэффициенты 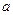и 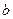неизвестны.

2.Предполагается, что ошибка при измерении величины 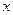, значительно (по крайней мере,

на порядок) меньше ошибки при измерении величины y . Поэтому погрешностью в

измерении 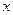можно прене­бречь.

З.Для определения 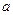и 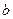выполняем 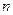пар измерений

4.Если считать, что 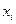- точное значение, то ему должно соответствовать значение

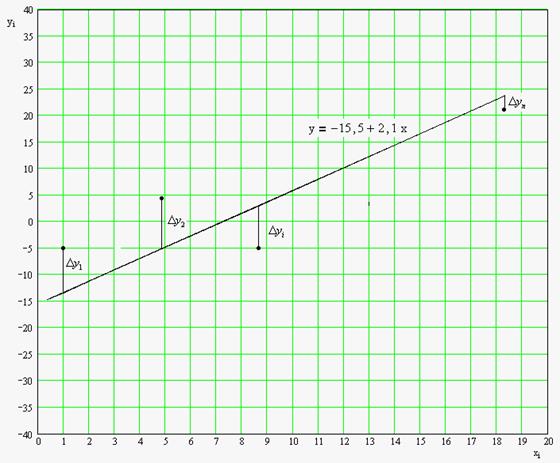
y_i ,равное 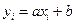; а в экспери­менте получено другое значение y_i , которое, вообще

говоря, не совпа­дает с 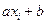. (см. график)

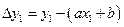расстояние первой точки от предполагаемой прямой

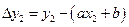расстояние второй точки от предполагаемой прямой

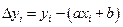расстояние i -ой точки от предполагаемой прямой

……………………………………………………………………………….

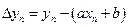расстояние n-ой точки от предполагаемой прямой

5.Согласно теории метода, значения a и b следует опреде­лять следующим образом.

Т.к. эти расстояния будут встречаться как с положительным, так и с отрицательным

знаком необходимо взять сумму квадратов этих расстояний

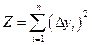
Это выражение по смыслу представляет собой сумму квадратов отклонений измерен­ных y_i от истинных. В методе наименьших квадратов утвержда­ется, что наилучшими оценками истинных значений коэффициентов 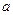и 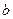служат значения, обеспечивающее минимум величины 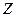(отсюда название метода). Должны выполняться условия:

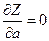и .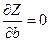

Найдем эти частные производные и приравняем их нулю.

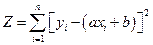
1)

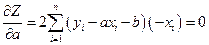
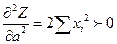
2)

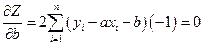
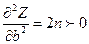
Т.к. вторые производные больше 0, функция 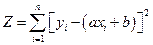, при найденных

a и b, будет минимальна.

Из первого уравнения получаем

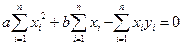
Из второго

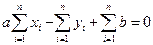или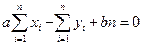

Отсюда 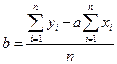(15)

Подставляя найденное 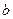в первое уравнение, получим:

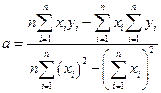(16)

На практике сначала находят коэффициент 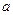затем коэффициент .

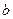Пример 7

Заданы 10 пар измеренных значений x_i и y_i

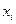	13.68	3.08	0.97	0.37	12.95	18.28	8.63	4.85	13.08	0.46
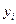	32.04	-4.74	-4.93	-21.90	3.35	21.09	-5.06	4.41	6.77	-38.41

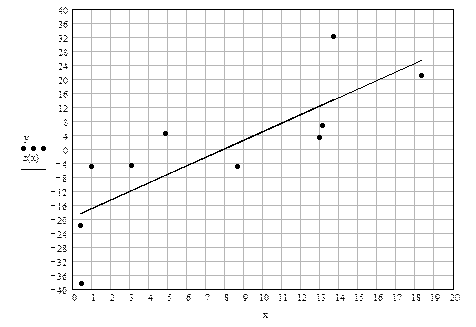
Наносим эти точки на график (см. рис.3). Точки имеют значительный разброс и «на глаз» провести усредняющую прямую невозможно.

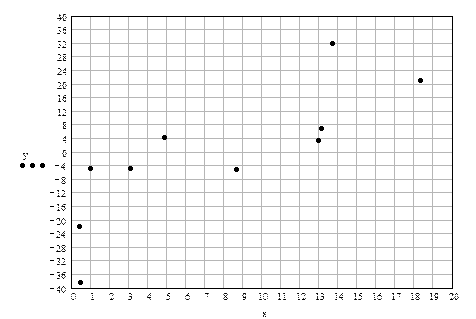
Рис.3

Заполняем таблицу.

№
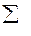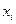	13.68	3.08	0.97	0.37	12.95	18.28	8.63	4.85	13.08	0.46	76.35
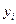	32.04	-4.74	-4.93	-21.90	3.35	21.09	-5.06	4.41	6.77	-38.41	-7.38
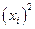	187,14	9,49	0,94	0.14	167.76	334.26	74.55	23.54	171.09	0.21	968.87
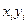	438.26	-14.61	-4.78	-8.14	43.35	385.50	-43.71	21.39	88.60	-17.55	888.33

Последний столбец таблицы используют для нахождения коэффициентов 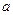и 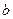по формулам (16) и (15). В нашем случае a = 2,45 b = -19,43

По найденным коэффициентам на графике по двум произвольно взятым значениям 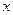и 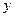строят прямую линию, y = 2,45 x – 19,43, которая является наилучшим усреднением экспериментальных точек.

Если зависимость между исследуемыми величинами нелинейная, то путем замены переменных ее можно преобразовать к линейной, после чего можно воспользоваться изложенным методом.

В качестве примера рассмотрим обработку экспериментальных данных при проведении лабораторной работы «Методы измерения температур».

В работе снимается зависимость сопротивления термистора r от температуры T, которая определяется с помощью термопары. Эта зависимость не линейная и имеет вид:

,

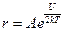где: А - некоторая постоянная; U-энергия активации; T-абсолютна температура; к - постоянная Больцмана. Применить метод наименьших квадратов для обработки результатов сразу нельзя. Преобразуем эту зависимость в линейную. Логарифмируя левую и правую часть, получим:

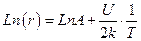
Как видно, теперь существует линейная зависимость между 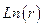и .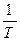

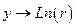
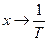
Полученные экспериментальные данные занесем в первые две строки таблицы.

Заполним оставшиеся строки таблицы.

№
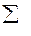r, кОм	3.000	3.556	4.250	5.143	6.333	8.000	10.500	14.667	23.000	--------
T,K	381.2	378.4	372.8	367.2	360.2	350.4	342.0	332.2	319.6	--------
1/T *10 3 ,1/K	2.623	2.643	2.682	2.723	2.776	2.854	2.924	3.010	3.129	25.365
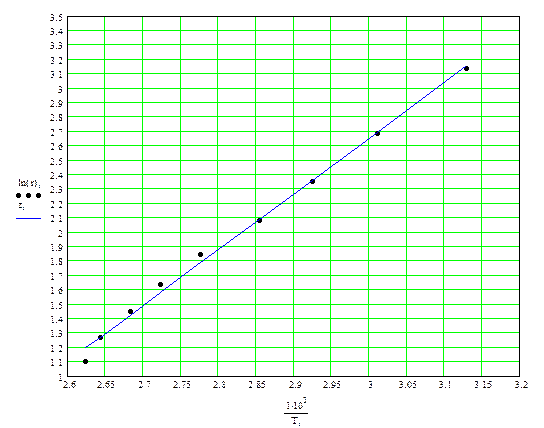
Ln(r)	1.099	1.269	1.447	1.638	1.846	2.079	2.351	2.686	3.135	17.549
(1/T*10 3) 2 ,1/K 2	6.882	6.984	7.195	7.416	7.707	8.145	8.550	9.062	9.790	71.731
Ln(r)* 1/T *10 3	2.882	3.352	3.881	4.460	5.124	5.934	6.875	8.084	9.811	50.404

Данные, представленные в 4 и 5 строках таблицы нанесем на график. Точки имеют некоторый разброс, но так как зависимость теперь линейная, можно применить метод наименьших квадратов.

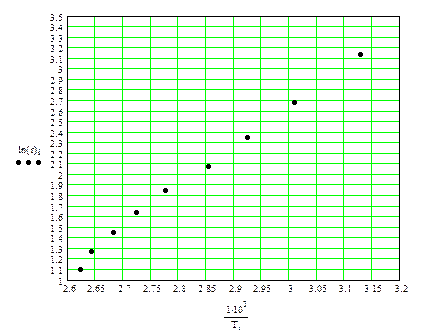
Заполняем 6 и 7 строки таблицы и рассчитываем коэффициенты a и b

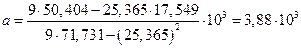
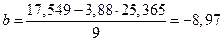
По найденным коэффициентам проводим прямую, усредняющую экспериментальные точки.