Вынуждающей силой. Резонанс скорости
Уравнение скорости vx(t) получим, дифференцируя уравнение смещения x(t) = Хcos (wt - j) по времени:
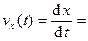
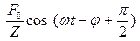 = wX
= wX 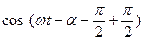 = wX
= wX 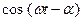 ,
,
где V = 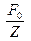 = wX – амплитуда скорости. Скорость vx(t) =wX
= wX – амплитуда скорости. Скорость vx(t) =wX 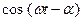 и вынуждающая сила Fx(t) = F0 coswt сдвинуты по фазе по отношению друг к другу на угол a. Фаза a может принимать значения от (
и вынуждающая сила Fx(t) = F0 coswt сдвинуты по фазе по отношению друг к другу на угол a. Фаза a может принимать значения от ( 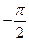 ) до (+
) до (+ 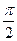 ) радиан. При условии
) радиан. При условии 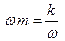 фаза a = 0. В этом случае частота вынуждающей силы w равна собственной частоте w0, и между скоростью и вынуждающей силы отсутствует сдвиг фаз. При a = 0 механический импеданс приобретает минимальное значение и равен только его активной части:
фаза a = 0. В этом случае частота вынуждающей силы w равна собственной частоте w0, и между скоростью и вынуждающей силы отсутствует сдвиг фаз. При a = 0 механический импеданс приобретает минимальное значение и равен только его активной части:
Z = 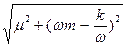 = m.
= m.
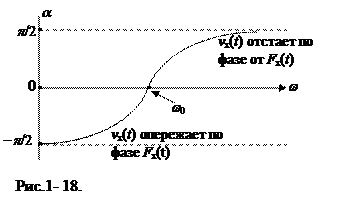 На рис. 18 приведен график зависимости разности фаз между скоростью и вынуждающей силой. Так как при
На рис. 18 приведен график зависимости разности фаз между скоростью и вынуждающей силой. Так как при 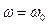 механический импеданс r минимален, то в этом случае амплитудное значение скорости приобретает максимальное значение из всех возможных, т.е. наблюдается резонанс скорости. Резонансное значение скорости
механический импеданс r минимален, то в этом случае амплитудное значение скорости приобретает максимальное значение из всех возможных, т.е. наблюдается резонанс скорости. Резонансное значение скорости
Vр. = 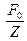 =
= 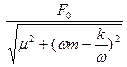 =
= 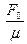 . (14)
. (14)
На рис.19приведен график зависимости амплитуды скорости смещения V от частоты вынуждающей силы w – график функции
V(w) = 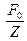 =
= 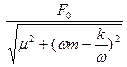 .
.
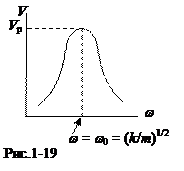 Из выражения для амплитуды скорости V =
Из выражения для амплитуды скорости V = 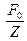 следует феноменологический смысл механического импеданса: механический импеданс Z =
следует феноменологический смысл механического импеданса: механический импеданс Z = 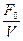 - это сила, которая необходима для сообщения колебательной системе единичной амплитудной скорости.
- это сила, которая необходима для сообщения колебательной системе единичной амплитудной скорости.
Всегда полезно результаты тех или иных расчетов представлять в разных формах, что позволяет более полно раскрыть содержание утверждений теории. Подставим в исходное дифференциальное уравнение 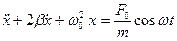 уравнения ускорения ax(t) º
уравнения ускорения ax(t) º  , скорости vx(t) º
, скорости vx(t) º  и смещения смещение x(t):
и смещения смещение x(t):
w2Xcos (wt - j + p ) + 2bwX 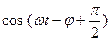 +
+ 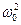 Хcos (wt - j) =
Хcos (wt - j) = 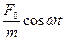 .
.
На векторной диаграмме член 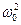 Хcos (wt - j) направим по лучу отсчета (рис. 20). Этому члену на диаграмме соответствует вектор, модуль которого равен
Хcos (wt - j) направим по лучу отсчета (рис. 20). Этому члену на диаграмме соответствует вектор, модуль которого равен 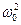 Х. Тогда векторная диаграмма члена 2bwX
Х. Тогда векторная диаграмма члена 2bwX 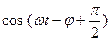 будет повернута против часовой стрелки на
будет повернута против часовой стрелки на 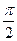 радиан. Этому члену на диаграмме
радиан. Этому члену на диаграмме
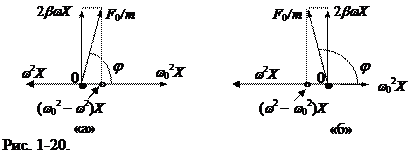
соответствует вектор, модуль которого равен 2bwX. Векторная диаграмма члена w2Xcos (wt - j + p ) будет повернута на p радиан. Этому члену соответствует вектор, модуль которого равен w2X. Модуль результирующего вектора равен 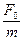 и повернут относительно вектора смещения на угол j. В зависимости от соотношений между w2X и
и повернут относительно вектора смещения на угол j. В зависимости от соотношений между w2X и 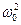 Х угол j может принимать значения от 0 до p (рис. 1-20 а, б). Из диаграммы следует выражение для тангенса разности фаз j: tg j =
Х угол j может принимать значения от 0 до p (рис. 1-20 а, б). Из диаграммы следует выражение для тангенса разности фаз j: tg j = 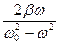 .
.
1.1.8. Устойчивость амплитуды вынужденных колебаний
В установившемся режиме работа вынуждающей силы должна компенсировать работу силы сопротивления: в течении периода Т = 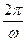 работа силы сопротивления Fсопр. = mvx должна быть равна работе вынуждающей силы Fx = F0 cos wt.
работа силы сопротивления Fсопр. = mvx должна быть равна работе вынуждающей силы Fx = F0 cos wt.
Вычислим работу через мощность силы: dA = Ndt = Fvxdt. Определим работу вынуждающей силы АB за период Т:
AB = 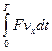 =
= 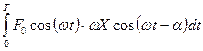 = p F0 X cosa . (15)
= p F0 X cosa . (15)
Работа AB идет на увеличение энергии осциллятора. Таким образом, за период T энергия осциллятора увеличивается на величину
ET = p F0 X cosa = 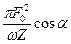 , где cosa =
, где cosa = 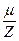 (15*)
(15*)
Работа силы сопротивления Асопр. за период колебаний равна:
Асопр. = 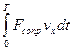 =
= 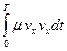 =
= 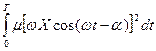 = p m wX2. (16)
= p m wX2. (16)
Поступающая в осциллятор энергия идет на работу против сил сопротивления. В установившемся режиме AB = Асопр.. Этому условию и должна удовлетворять амплитуда установившихся вынужденных колебаний. Учитывая условие AB = Асопр., получим выражение для амплитуды установившихся вынужденных колебаний в виде:
X = 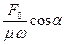 . (17)
. (17)
Вследствие того, что амплитуда неотрицательная величина, то cosa = 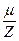 в (17) берется по модулю. Кроме того, получим, что X =
в (17) берется по модулю. Кроме того, получим, что X = 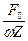 , что, разумеется, совпадает с ранее полученным выражением для амплитуды смещения.
, что, разумеется, совпадает с ранее полученным выражением для амплитуды смещения.
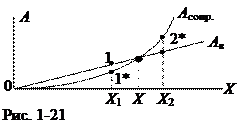 На рис. 21 приведены два графика: график работы вынуждающей силы AB(Х) при некотором значении a и график работы силы сопротивления Асопр(Х). Работа вынуждающей силы пропорциональна амплитуде смещения Х, а работа силы сопротивления пропорциональна квадрату амплитуды X2. Следовательно, графики AB(Х) и Асопр.(Х) пересекаются. Точка пересечения графиков соответствует установившемуся режиму вынужденных колебаний, т.е. условию AB = Асопр..
На рис. 21 приведены два графика: график работы вынуждающей силы AB(Х) при некотором значении a и график работы силы сопротивления Асопр(Х). Работа вынуждающей силы пропорциональна амплитуде смещения Х, а работа силы сопротивления пропорциональна квадрату амплитуды X2. Следовательно, графики AB(Х) и Асопр.(Х) пересекаются. Точка пересечения графиков соответствует установившемуся режиму вынужденных колебаний, т.е. условию AB = Асопр..
Установившаяся амплитуда вынужденных колебаний обладает устойчивостью. Действительно, допустим, по какой-либо причине амплитуда уменьшилась до значения Х1. В этом случае работа вынуждающей силы, которая отображена на графике точкой 1, превосходит работу силы сопротивления, которая отображена точкой 1*. Это приводит к увеличению амплитуды до первоначального устойчивого значения Х. Если амплитуда случайным образом увеличивается до Х2, то работа силы сопротивления (точка 2*) становится больше работы вынуждающей силы (точка 2), что приводит к уменьшению амплитуды до устойчивого значения Х.
1.1.9. Добротность осциллятора
Выражение для добротности колебательной системы (осциллятора) приведено в § 1.1.4: Q = 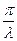 = pNe. Добротность Q выражена как число пропорциональное числу колебаний Ne, которое совершает осциллятор в отсутствии внешней вынуждающей силы за время релаксации t. Время релаксации t =
= pNe. Добротность Q выражена как число пропорциональное числу колебаний Ne, которое совершает осциллятор в отсутствии внешней вынуждающей силы за время релаксации t. Время релаксации t = 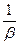 =
= 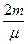 секунд. Напомним, за время релаксации t амплитуда затухающих колебаний уменьшается в e ≈ 2,7 раз. Определим содержание понятия добротности из энергетических представлений.
секунд. Напомним, за время релаксации t амплитуда затухающих колебаний уменьшается в e ≈ 2,7 раз. Определим содержание понятия добротности из энергетических представлений.
Первоначальная энергия, содержащаяся в осцилляторе, затрачивается на работу против сил сопротивления, что и приводит к затуханию колебаний в отсутствии внешней вынуждающей силы. В этой связи добротность Q можно рассматривать как характеристику быстроты уменьшения энергии осциллятора при затухающих колебаниях.
При затухающих колебаниях x(t)= A 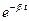 cos (w/t + a) амплитуда уменьшается по закону A
cos (w/t + a) амплитуда уменьшается по закону A 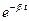 = A
= A 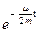 . Здесь A – начальная амплитуда осциллятора, a - начальная фаза, w/ =
. Здесь A – начальная амплитуда осциллятора, a - начальная фаза, w/ = 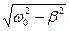 =
= 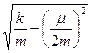 - частота затухающих колебаний и 2b =
- частота затухающих колебаний и 2b = 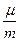 . Энергия осциллятора E пропорциональна квадрату амплитуды A2
. Энергия осциллятора E пропорциональна квадрату амплитуды A2 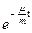 :
:
E = E0 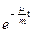 . (18)
. (18)
Из (18) видно, что за время t = 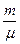 =
= 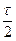 энергия осциллятора становится равной
энергия осциллятора становится равной 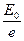 , т.е. уменьшается в e ≈ 2,7 раз. За время t =
, т.е. уменьшается в e ≈ 2,7 раз. За время t = 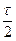 =
= 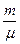 осциллятор совершит
осциллятор совершит 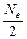 колебаний, и фаза изменится на величину w/t = w/
колебаний, и фаза изменится на величину w/t = w/ 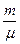 радиан. Добротность определяется как число радиан, на которое изменяется фаза затухающих колебаний при уменьшении энергии осциллятора в e ≈ 2,7 раз:
радиан. Добротность определяется как число радиан, на которое изменяется фаза затухающих колебаний при уменьшении энергии осциллятора в e ≈ 2,7 раз:
Q = 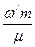 .
.
В обычных колебательных системах коэффициент затухания много меньше собственной частоты системы w0 >> b, поэтому можно приблизительно считать, что w/ ≈ w0 = 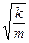 .
.
В этом приближении добротность примет вид:
Q = 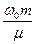 или (19)
или (19)
Q = 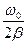 =
= 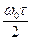 . (19*)
. (19*)
где t - время релаксации, за которое осциллятор успевает совершить Ne колебаний. Добротность является одной из важных собственных характеристик колебательной системы.
Покажем, что из (19) следует формула: Q = p Ne. Если в некоторый момент времени смещение принимает, например, амплитудное значение, то при изменении фазы колебания на 2p радиан, смещение вновь принимает амплитудное значение. Отношение 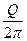 =
= 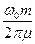 , но w0 =
, но w0 = 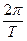 и
и 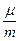 = 2b =
= 2b = 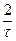 , поэтому
, поэтому 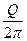 =
= 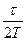 . За время релаксации t осциллятор совершает Ne колебаний, т.е. Ne =
. За время релаксации t осциллятор совершает Ne колебаний, т.е. Ne = 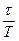 , где T - период колебаний, следовательно:
, где T - период колебаний, следовательно: 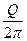 =
= 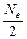 или
или
Q = p Ne.
1.1.10. Добротность и резонансная кривая поглощения
Осциллятора
Как видно из формулы (19), добротность определяется собственной частотой w0 и активной составляющей импеданса m (сопротивлением среды). Получим еще одно выражение для добротности осциллятора, непосредственно связанное с зависимостью поглощения энергии осциллятором от частоты вынуждающей силы.
Предварительно определим энергию, передаваемую вынуждающей силой осциллятору, за единицу времени. За период осциллятор получает энергию, определяемую выражением (15*), см. § 1.1.8. За единицу времени энергия, передаваемая осциллятору (мощность P, передаваемая осциллятору), равна P = 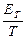 =
= 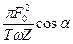 =
= 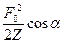 =
= 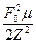 , (20)
, (20)
 т.к. w =
т.к. w = 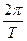 и cosa =
и cosa = 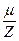 =
= 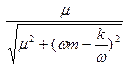 (см. рис. 13 и 14). Импеданс минимален при условии
(см. рис. 13 и 14). Импеданс минимален при условии 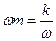 (т.е. при
(т.е. при 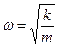 = w0). При этом условии Z = m и осциллятору передается максимальная мощность. При w = w0 наблюдается резонансное поглощение энергии. Резонансная мощность поглощения принимает вид:
= w0). При этом условии Z = m и осциллятору передается максимальная мощность. При w = w0 наблюдается резонансное поглощение энергии. Резонансная мощность поглощения принимает вид:
Pр = 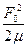 . (24)
. (24)
Напомним, при условии w = w0 наблюдаем резонанс скорости (см § 1.1.7, рис. 1-19). Таким образом, при максимальной скорости осциллятора (при резонансе скорости) наблюдается максимальное поглощение энергии (резонанс мощности поглощения), передаваемое осциллятору внешней вынуждающей силой. На рис. 22 приведена кривая зависимости мощности поглощения от частоты вынуждающей силы, определяемая формулой (20). На рисунке частоты w1 и w2 соответствуют мощности поглощения, которая равна половине резонансной мощности.
Покажем, что добротность осциллятора можно выразить отношением: Q = 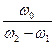 . Попутно заметим, разность частот (w2 -w1) определяет остроту резонансной кривой по мощности (или, как говорят, остроту резонансного максимума).
. Попутно заметим, разность частот (w2 -w1) определяет остроту резонансной кривой по мощности (или, как говорят, остроту резонансного максимума).
Частоты w1 и w2 находим из условия 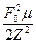 =
= 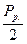 =
= 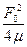 . Отсюда следует, что при частотах w1 и w2 имеем равенство: Z2 = 2m2. Из равенства
. Отсюда следует, что при частотах w1 и w2 имеем равенство: Z2 = 2m2. Из равенства 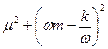 = 2m2 получим:
= 2m2 получим: 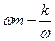 = ± m или
= ± m или
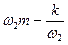 = +m и
= +m и 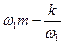 = -m (w2 >w1)
= -m (w2 >w1)
Исключив из этих уравнений жесткость k, получим: w2 -w1= 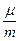 .
.
Подставим значение разности частот в формулу добротности (19):
Q = 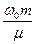 =
= 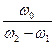 =
= 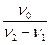 . (21)
. (21)
Разность частот (w2 -w1) называют частотной шириной поглощения.
Итак, по остроте резонансной кривой поглощения можно судить о добротности колебательной системы: чем острее резонанс, т.е. чем меньше частотная ширина поглощения (w2 -w1), тем добротнее осциллятор. Например, добротность кварцевого резонатора, используемого в прецизионных генераторах радиочастотного диапазона, достигает значений ~106. У таких резонаторов при n0 = 1МГц ширина частоты поглощения ~ 1Гц.
При частотах вынуждающей силы w1 и w2 осциллятор поглощает в единицу времени энергию, равную половине резонансной мощности поглощения при w0. Определим значения амплитуды скорости на частотах w1 и w2 и сравним их с резонансной амплитудой скоростью Vp..
Амплитуда скорости определяется выражением V = 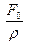 = wX, а резонансная скорость Vр. =
= wX, а резонансная скорость Vр. = 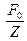 =
= 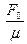 . Так как
. Так как 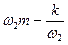 = +m и
= +m и 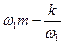 = -m, то при частотах w1 и w2 импеданс имеет вид: Z =
= -m, то при частотах w1 и w2 импеданс имеет вид: Z = 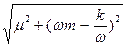 = m
= m 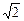 . Отсюда следует, что при частотах w1 и w2 амплитудное значение скорости:
. Отсюда следует, что при частотах w1 и w2 амплитудное значение скорости:
V = 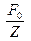 =
= 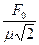 =
= 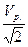 . (22)
. (22)
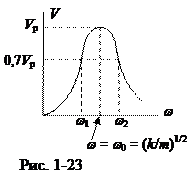 Величина
Величина 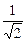 ≈ 0,707. Интервал (w2 -w1) на уровне 0,7 называют еще частотной шириной пропускания колебательной системы по скорости (рис. 23). Именно в интервале этих частот вынуждающей силы колебательная система отвечает на внешнее воздействие заметной скоростью. Если частота w вынуждающей силы F = F0 cos wt окажется вдали от интервала частот (w2-w1), то колебательная система практически не реагирует на такое внешнее воздействие.
≈ 0,707. Интервал (w2 -w1) на уровне 0,7 называют еще частотной шириной пропускания колебательной системы по скорости (рис. 23). Именно в интервале этих частот вынуждающей силы колебательная система отвечает на внешнее воздействие заметной скоростью. Если частота w вынуждающей силы F = F0 cos wt окажется вдали от интервала частот (w2-w1), то колебательная система практически не реагирует на такое внешнее воздействие.
