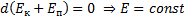Динамика переменной массы. Уравнение движения тела переменной массы. Уравнение Циолковского
Вывод уравнения движения тела переменной массы на примере движения ракеты:
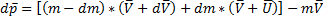 ,
,
Где 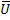 - скорость истечения газов относительно ракеты. Тогда:
- скорость истечения газов относительно ракеты. Тогда:
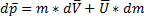
Если на систему действуют внешние силы, то изменение импульса должно быть равно импульсу внешних сил:
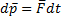
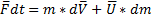
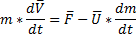
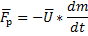
Fр – реактивная сила.
Уравнение движения тела переменной массы (уравнение И.В.Мещерского ):
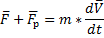
Если F=0, то:
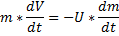
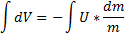
Уравнение Циалковского:
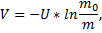
Где m0 – начальная масса ракеты, m – конечная масса ракеты.
Механическая энергия и работа. Работа переменной силы. Мощность. Работа консервативных сил.
Энергия – скалярная величина, является единой мерой различных форм движения. Любое тело обладает запасом энергии.
Работа силы – изменение энергии, происходящее под действием сил, приложенных к телу.
∆E=A
Элементарная работа силы 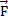 на малом перемещении d
на малом перемещении d  :
:
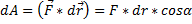 ;
;
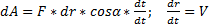 ;
;
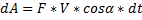 ;
;
В прямоугольной системе координат элементарная работа dA равна:
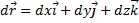 ;
;
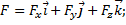 Fr
Fr
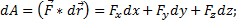
Работа на конечном участке траектории:
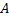 12=
12= 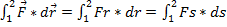 ;
;
[dA]=Н*м=Дж (Джоуль)
Мощность – интенсивность совершаемой работы (работа в единицу времени)
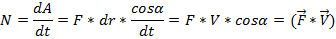
Если N постоянно, то:
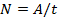
[N]=Дж/с=Вт (Ватт)
Консервативная сила (потенциальная) – такая сила, работа которой зависит от формы пути тела.
Например: гравитационные силы, упругие силы, кулоновские силы.
При перемещении вдоль замкнутой траектории работа консервативной силы равна нулю.
Кинетическая энергия системы и её связь с работой внутренних и внешних сил.
Кинетическая энергия – энергия механического движения, или энергия скорости.
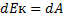
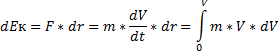
Eк=mV2/2
A12=Eк2-Eк1
Eк механической системы тел равна сумме Eк всех тел системы.
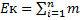 iV2i /2
iV2i /2
Понятия поля и потенциальной энергии частицы в силовом поле. Потенциальная энергия частицы поднятой на высоту h.
Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и положением во внешнем силовом поле (гравитационная, электростатическая и тд).
Применим только к системе тел под действием консервативных сил.
Взаимодействие сил осуществляется под действием силового поля.
Потенциальная энергия тела массой m поднятого на высоту h:
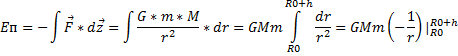
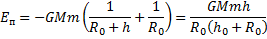
Если h0<<R0, то:
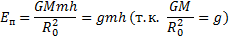
Механическая энергия. Законы сохранения и изменения энергии в механике.
Механическая энергия – сумма кинетической и потенциальной энергий тела.
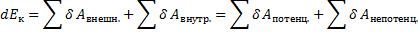
Т.к. 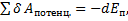
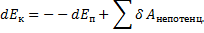
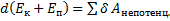 (Закон изменения полной механической энергии)
(Закон изменения полной механической энергии)
Если система неконсервативная, то Aнепотенц.=0
В неконсервативных системах полная механическая энергия сохраняется: