Стационарная теплопередача через цилиндрическую стенку

Рассмотрим однородную цилиндрическую стенку (трубу) с внутренним диаметром d₁ и наружным – d₂, длина которой L много больше толщины стенки (рис. 3.4). Коэффициент теплопроводности l материала стенки постоянен.

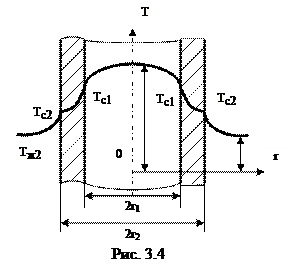Заданы постоянные температуры движущихся внутри и снаружи трубы жидкостей Т_ж1 и Т_ж2 и постоянные значения коэффициентов теплоотдачи на внутренней и наружной поверхностях трубы a₁ и a_2. Необходимо определить линейную плотность потока тепла q_L и температуры на поверхностях стенки Т_С1 и Т_С2.

Так как линейная плотность теплового потока, подводимого к стенке, прошедшего через стенку и отводимого от стенки одна и та же, то можно записать систему равенств

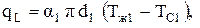
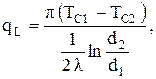
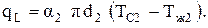
Если переписать эту систему равенств так, чтобы справа остались только температурные разности, а затем сложить левые и правые части, то все температуры в правой части сократятся, кроме первой и последней. Для линейной плотности теплового потока получим формулу

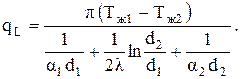(3.41)

Если полученное по (3.41) значение q_L подставить в выписанные выше равенства, то можно определить температуры Т_С1 и Т_С2. Обозначим:

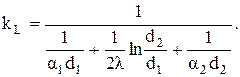(3.42)

Величина k_L называется линейным коэффициентом теплопередачи и измеряется в Вт/(м×град). Величина R_L=1/k_L, м×град/Вт, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи

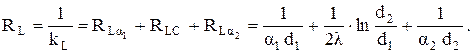(3.43)

Оно представляет сумму линейных термических сопротивлений соответственно в формуле: линейного термического сопротивления теплоотдачи на внутренней поверхности стенки, линейного термического сопротивления теплопроводности стенки и линейного термического сопротивления теплоотдачи на наружной поверхности стенки. Если тепловой поток отнести к внутренней или наружной поверхности, то получим соответственно плотности теплового потока на этих поверхностях

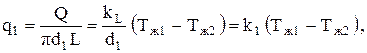
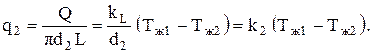
Коэффициенты теплопередачи, соответственно при отнесении потока тепла к внутренней и наружной поверхностям, имеют вид

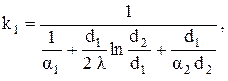
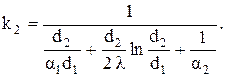
На практике часто встречаются трубы, толщина стенок которых мала по сравнению с диаметром. В этом случае приведенные выше формулы упрощаются. Действительно, если разложим в ряд

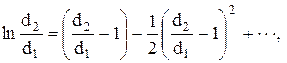
то при d₂/d₁®1 такой ряд быстро сходится, и с достаточной точностью можно ограничиться первым членом ряда

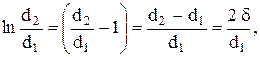
где d – толщина цилиндрической стенки.

Если это значение подставить в выражение для k₁, то получим

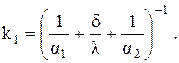
Следовательно, если стенка трубы тонкая, то для практических расчетов можно использовать формулу

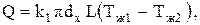(3.44)

где если a₁>>a₂, то d_x=d₂;

если a₂>>a₁, то d_x=d₁;

если a₁»a_2, то d_x=(d₁+d₂)/2.

Обычно в инженерных расчетах при d₂/d₁ £ 1,8 пользуются формулой (3.44). При этом относительная погрешность не превышает 4 %.

При теплопередаче через многослойную цилиндрическую стенку необходимо учесть линейные термические сопротивления теплопроводности каждого слоя. Тогда линейная плотность теплового потока равна

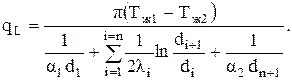(3.45)

После определения линейной плотности теплового потока по (3.45) температура на границе любых двух слоев i и i+1 рассчитывается по формуле

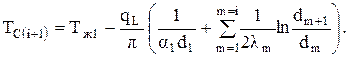(3.46)

Если в соотношениях (3.45) и (3.46) a₁=¥ и a₂=¥, то граничные условия третьего рода вырождаются в граничные условия первого рода, а соотношения (3.45) и (3.46) – в (3.36) и (3.37).