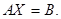Системы линейных алгебраических уравнений. Матрицы. Действия над матрицами
Матрицы. Действия над матрицами
Матрицей порядка 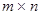 называется прямоугольная таблица чисел
называется прямоугольная таблица чисел
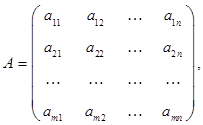
состоящая из m строк и n столбцов, рассматриваемая как единый алгебраический объект, над которым могут производиться определенные алгебраические действия. Часто пишут
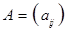 ,
, 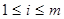 , 1
, 1 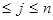 . Множество всех матриц порядка
. Множество всех матриц порядка 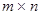 обозначим
обозначим 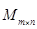 , множество всех квадратных матриц порядка
, множество всех квадратных матриц порядка 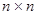 – через
– через 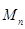 .
.
Произведением матрицы 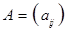
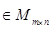 на число
на число 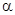 (действительное или комплексное) называют матрицу
(действительное или комплексное) называют матрицу 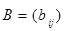
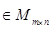 , определяемую по правилу
, определяемую по правилу 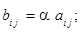 при этом пишут
при этом пишут 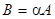 .
.
Суммой  матриц
матриц 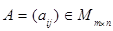 ,
, 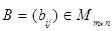 называют матрицу
называют матрицу 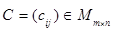 , определяемую по правилу
, определяемую по правилу 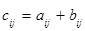 ; при этом пишут
; при этом пишут 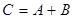 . Складывать можно лишь матрицы одинакового порядка.
. Складывать можно лишь матрицы одинакового порядка.
Произведением матрицы 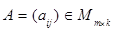 на матрицу
на матрицу 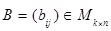 называют матрицу
называют матрицу 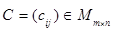 , элементы которой определяются по правилу
, элементы которой определяются по правилу 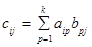 ; при этом пишут
; при этом пишут 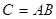 . Произведение матриц определено, если количество столбцов первого множителя А совпадает с количеством строк второго множителя В. (Можно сказать, что элемент
. Произведение матриц определено, если количество столбцов первого множителя А совпадает с количеством строк второго множителя В. (Можно сказать, что элемент 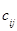 матрицы
матрицы 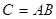 есть результат скалярного произведения i-й строки матрицы А на j-й столбец матрицы В.)
есть результат скалярного произведения i-й строки матрицы А на j-й столбец матрицы В.)
Введенные операции над матрицами обладают всеми известными свойствами суммы и произведения чисел
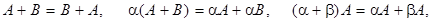
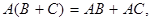
кроме одного: вообще говоря, 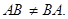
Матрицу
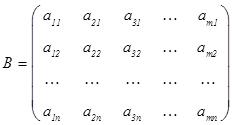
называют транспонированной к матрице А и пишут 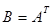 ;
; 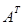 получается из А переменой местами столбцов и строк.
получается из А переменой местами столбцов и строк.
Нулевой матрицей (нуль-матрицей) называется матрица 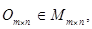 состоящая из нулей.
состоящая из нулей.
Единичной матрицей порядка 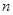 называется квадратная матрица
называется квадратная матрица 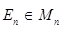 , на главной диагонали которой, тянущейся слева-сверху-вправо-вниз, находятся единицы, а остальные элементы равны 0:
, на главной диагонали которой, тянущейся слева-сверху-вправо-вниз, находятся единицы, а остальные элементы равны 0:
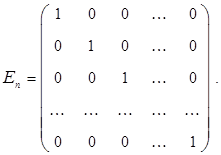
Часто пишут просто Е, опуская индекс n там, где это не приводит к недоразумению.
Матрицы О и Е играют роль нуля и единицы: 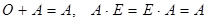 (операции считаются дозволенными).
(операции считаются дозволенными).
Квадратная матрица, у которой все элементы вне главной диагонали равны 0, называется диагональной. Квадратная матрица, у которой все элементы, расположенные ниже главной диагонали, равны 0, называется треугольной.
Задачи
Рассмотрим в аудитории типичные примеры, для решения которых используются приведенные определения и понятия.
1.Вычислить 3A – 2BC, если:
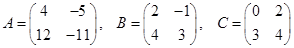 .
.
Ответ. 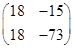 .
.
2.Вычислить:
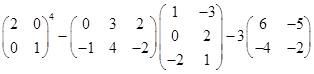 .
.
Ответ. 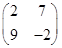 .
.
3.Вычислить: а) 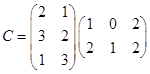 ; б)
; б) 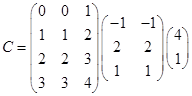 .
.
Ответ. а) 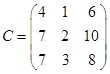 ; б)
; б) 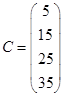 .
.
Задания для самостоятельного решения
1.Найти многочлен от матрицы А, если 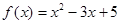 ,
, 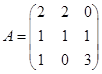 .
.
Ответ. 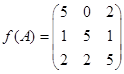 .
.
2.Найти 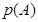 , если
, если 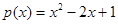 ,
, 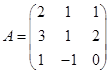 .
.
Ответ. 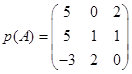 .
.
Обратная матрица
Матрица 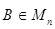 называется обратной к матрице
называется обратной к матрице 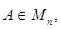 если AB = BA = Е; при этом пишут
если AB = BA = Е; при этом пишут 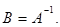 Матрица А имеет обратную только в том случае, если она невырожденная, то есть если
Матрица А имеет обратную только в том случае, если она невырожденная, то есть если 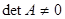 . Если
. Если 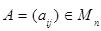 – невырожденная матрица, то
– невырожденная матрица, то
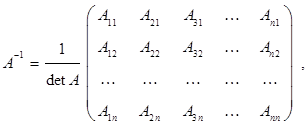
где 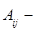 алгебраические дополнения элементов
алгебраические дополнения элементов 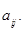
Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется система уравнений вида
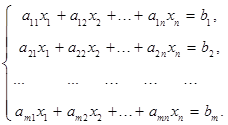
Система называется однородной, если свободные члены равны нулю: 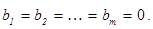 Однородная система всегда является совместной - она имеет решение
Однородная система всегда является совместной - она имеет решение 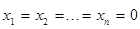 (возможно, не единственное).
(возможно, не единственное).
Матрицы
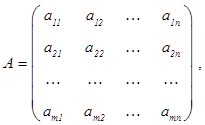
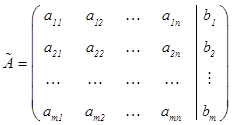 называются матрицей системы и расширенной матрицей системы соответственно; столбцы
называются матрицей системы и расширенной матрицей системы соответственно; столбцы 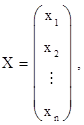
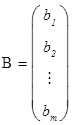 называются столбцом неизвестных и столбцом свободных членов соответственно. С учетом этих обозначений систему можно записать в матричной форме
называются столбцом неизвестных и столбцом свободных членов соответственно. С учетом этих обозначений систему можно записать в матричной форме